Как найти энергию связи атома. Энергия связи атомных ядер

Удельной энергией связи называют энергию связи, приходящуюся на один нуклон ядра. Ее определяют экспериментальным путем. Если разделить на полное число нуклонов в ядре А, то получится удельная энергия связи,

На рисунке 1 приведена зависимость экспериментальных значений от массового числа А. При рассмотрении этого рисунка можно сделать следующие выводы.

В самом деле, если бы каждый нуклон взаимодействовал со всеми остальными нуклонами ядра, то число таких парных взаимодействий было бы равно А(А-1)/2 и при Аи среднем значении энергии каждого парного взаимодействия ε полная энергия взаимодействия (в данном случае полная энергия связи ядра) была бы пропорциональна εи, стало быть, ВεА, т.е. возрастала бы линейно с ростом массового числа. Поскольку Вconst, приходиться допустить, что общее число связей пропорционально просто числу частиц А (а не ). Отсюда следует, что у каждого нуклона есть ограниченный запас возможностей взаимодействия, и если этот запас уже израсходован на связь с двумя – тремя соседними нуклонами, то наступает состояние насыщения и связи с другими нуклонами оказываются ослабленными даже на очень близких расстояниях.

Наиболее прочными являются ядра со средними массовыми числами (у них самые большие значения В).

В легких ядрах все или почти все нуклоны лежат на поверхности ядра и поэтому не в полной мере используют свои возможности взаимодействия, что несколько уменьшает значения В. С ростом А увеличивается доля нуклонов, лежащих внутри ядра, которые свои возможности взаимодействия используют полностью, поэтому значения В постепенно увеличиваются. Однако при дальнейшем увеличении числа нуклонов в ядре начинает все сильнее сказываться взаимное отталкивание электрических зарядов протонов, которое стремится разорвать ядро и поэтому уменьшает В. Это приводит к тому, что все тяжелые ядра оказываются нестабильными.

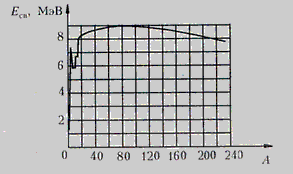
Рис.1

Расчет энергии связи ядра.

Энергия связи ядра численно равна работе, которую нужно затратить для расщепления ядра на отдельные нуклоны, или энергии, выделяющейся при синтезе ядер из нуклонов. Мерой энергии связи ядра является дефект массы.

Формула для расчета энергии связи ядра - это формула Эйнштейна: если есть какая-то система частиц, обладающая массой, то изменение энергии этой системы приводит к изменению ее массы.

Здесь энергия связи ядра выражена произведением дефекта масс на квадрат скорости света.

В ядерной физике массу частиц выражают в атомных единицах массы (а.е.м.).

Однако, в ядерной физике принято выражать энергию в электрон-вольтах (эВ):

Просчитаем соответствие 1 а.е.м. электрон-вольтам:

Теперь расчетная формула энергии связи (в электрон-вольтах) будет выглядеть так:

15. Примеры решения задач

1. Вычислить массу ядра изотопа .

Решение. Воспользуемся формулой

.

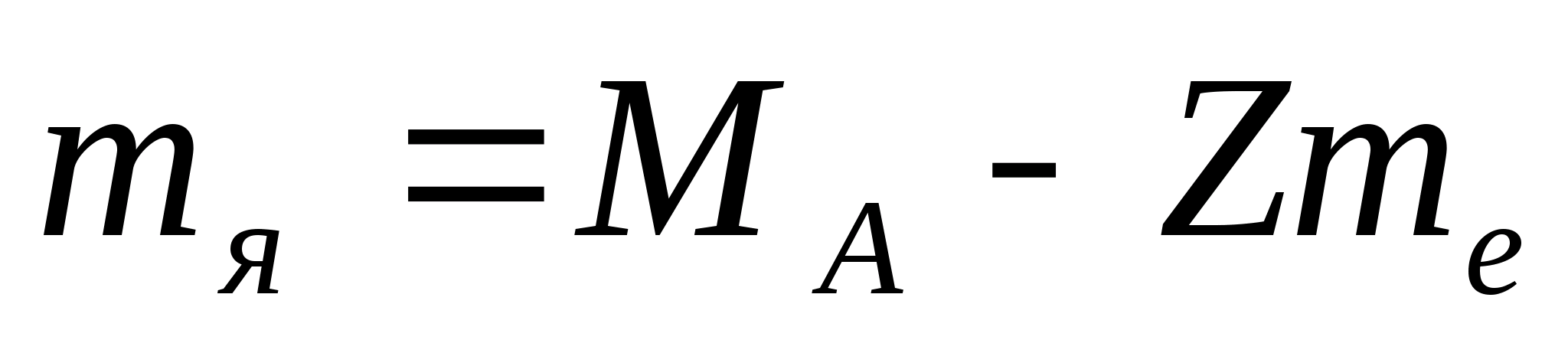Атомная масса кислорода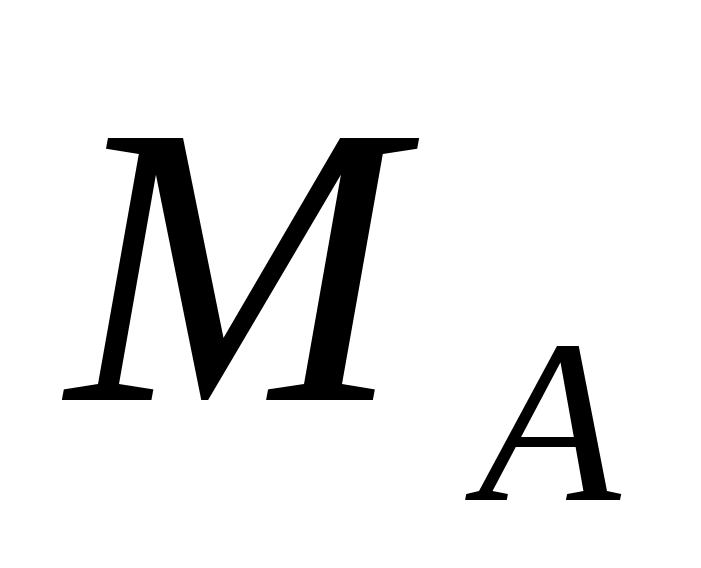

=15,9949 а.е.м.;

т.е. практически весь вес атома сосредоточен в ядре.

2. Вычислить дефект массы и энергию связи ядра 3 Li 7 .

Решение. Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра (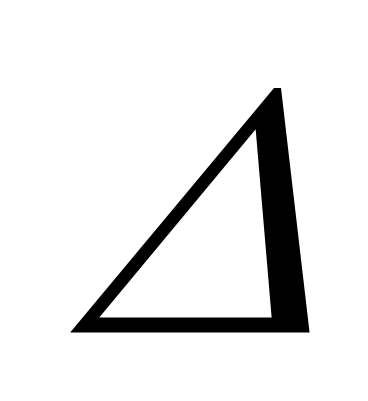m ) и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т.е.

где Z – атомный номер (число протонов в ядре); А – массовое число (число нуклонов, составляющих ядро); m p , m n , m – соответственно массы протона, нейтрона и ядра.

В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в неё входила масса М нейтрального атома.

,

.

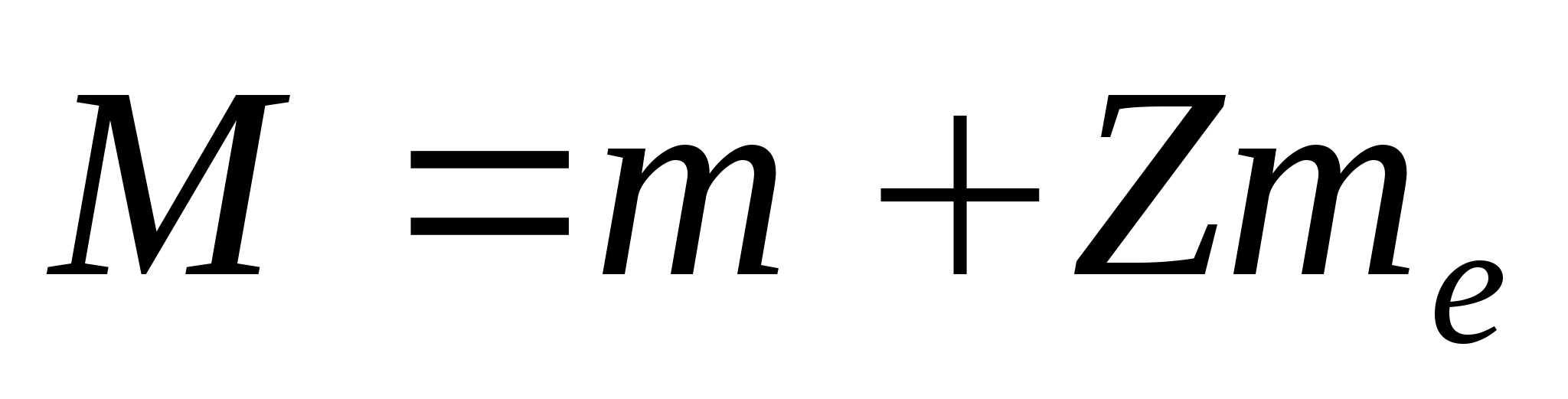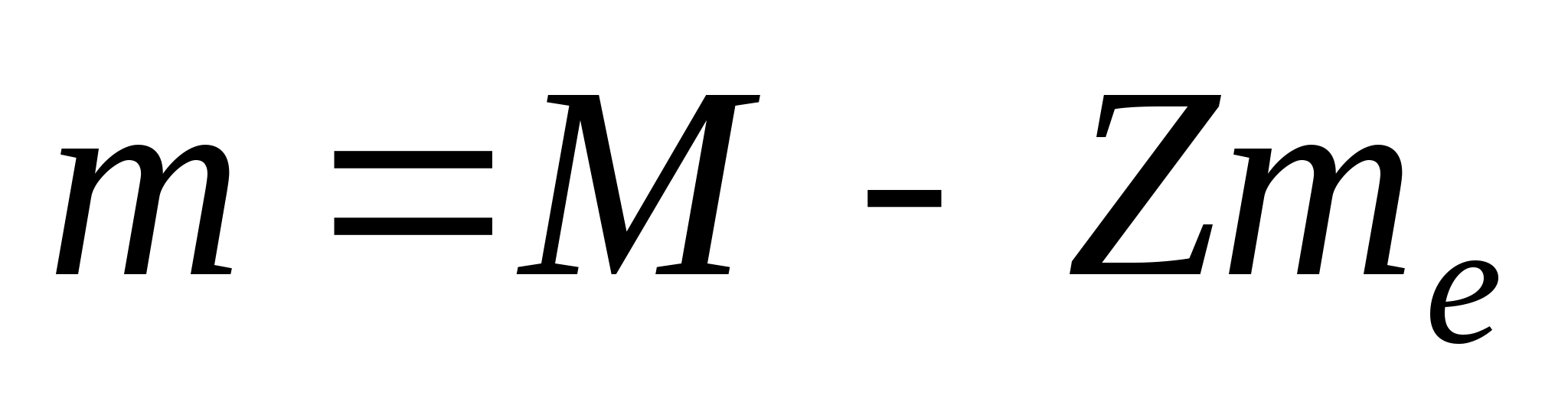Выразив в равенстве (1) массу ядра по последней формуле, получим

,

Замечая, что m p +m e =M H , где M H – масса атома водорода, окончательно найдём

Подставив в выражение (2) числовые значения масс (согласно данным справочных таблиц), получим

Энергией связи

ядра называется энергия, которая в той или иной форме выделяется при образовании ядра из свободных нуклонов.

В соответствии с законом пропорциональности массы и энергии

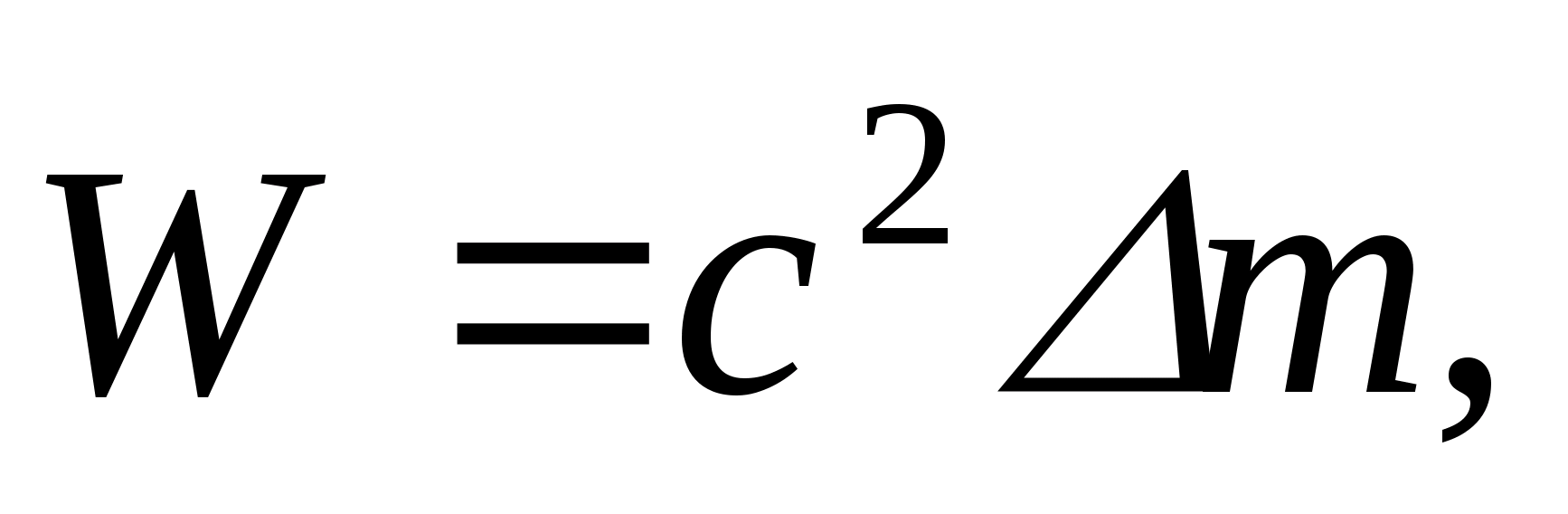(3)

где с – скорость света в вакууме.

Коэффициент пропорциональности с 2 может быть выражен двояко: или

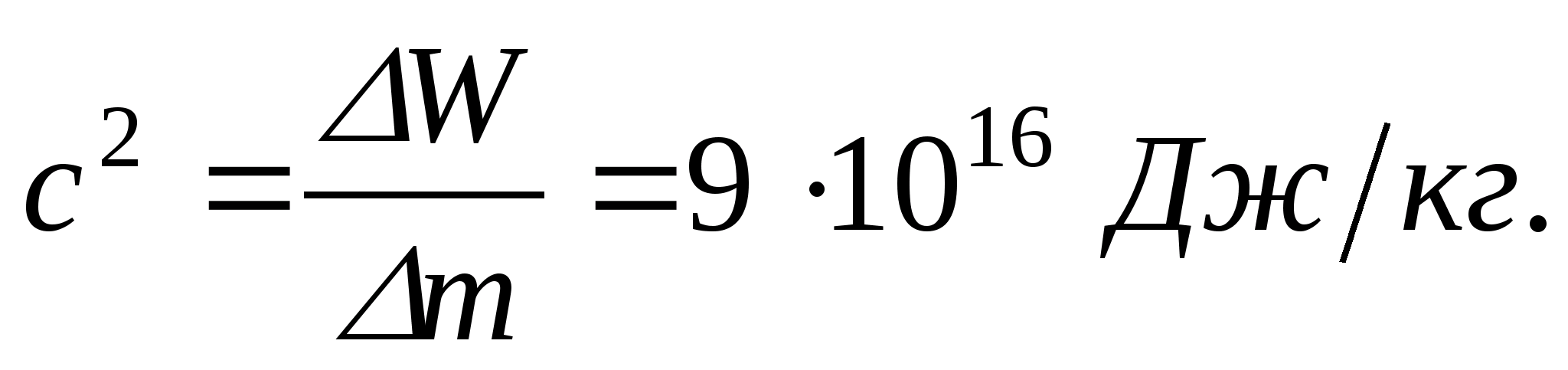
Если вычислить энергию связи, пользуясь внесистемными единицами, то

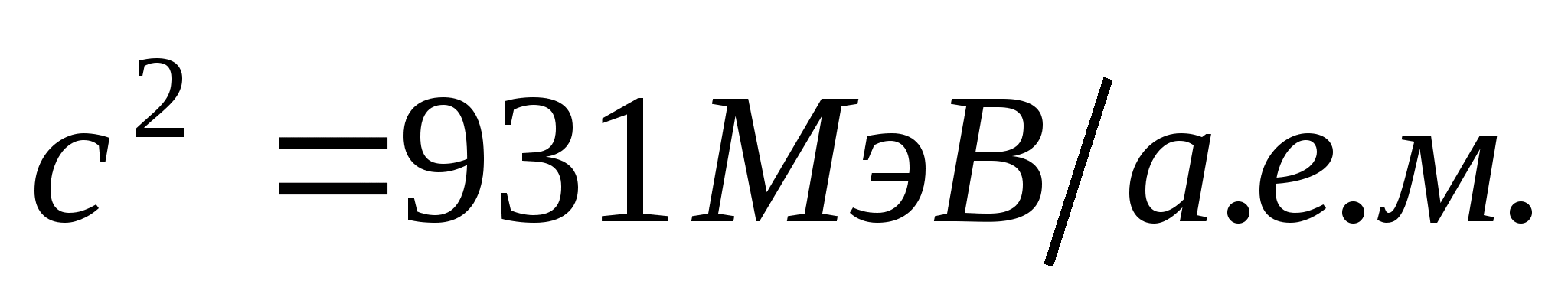
С учётом этого формула (3) примет вид

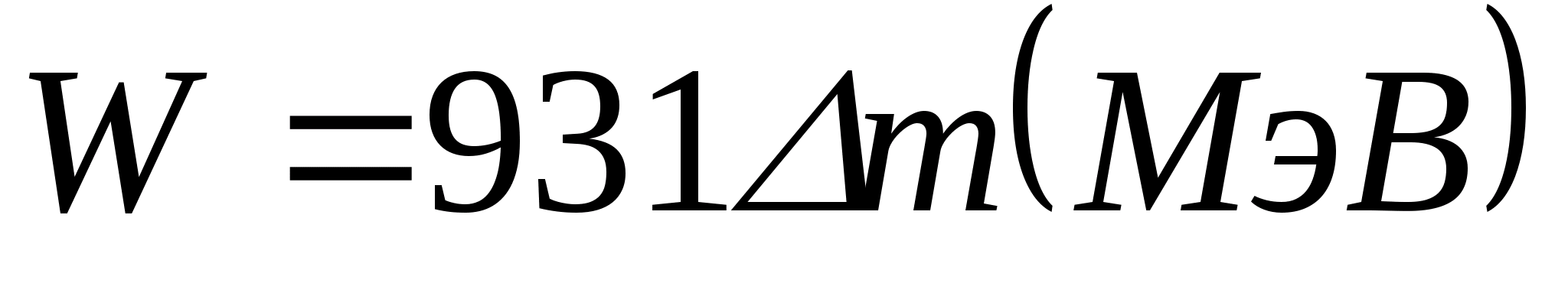(4)

Подставив ранее найденное значение дефекта массы ядра в формулу (4), получим

3. Две элементарные частицы – протон и антипротон, имеющие массу по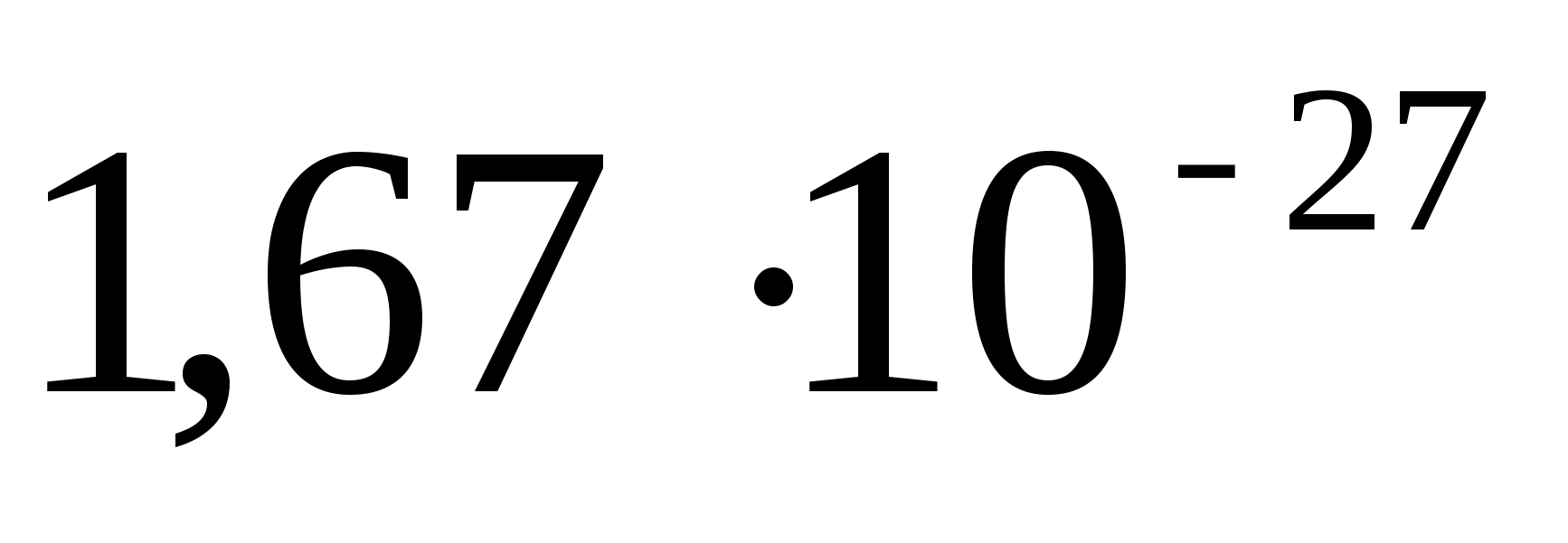

кг каждый, соединяясь, превращаются в два гамма – кванта. Сколько при этом освобождается энергии?

Решение. Находим энергию гамма – кванта по формуле Эйнштейна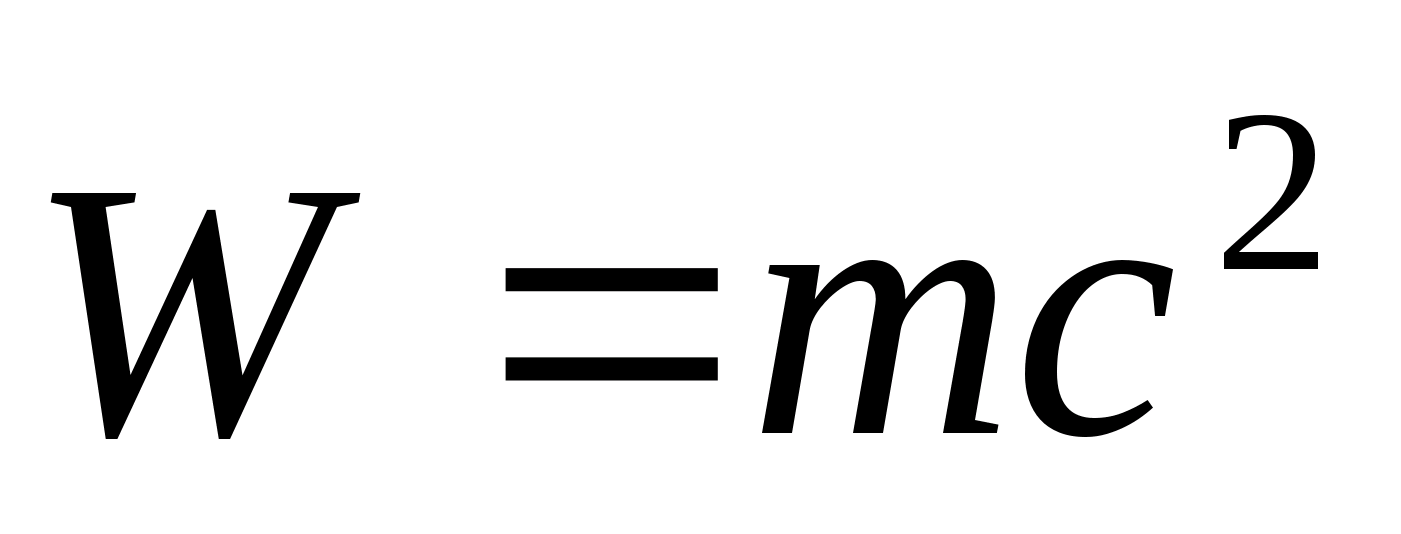

, где с – скорость света в вакууме.

4. Определить энергию, необходимую для разделения ядра 10 Ne 20 на ядро углерода 6 С 12 и две альфа-частицы, если известно, что удельные энергии связи в ядрах 10 Ne 20 ; 6 С 12 и 2 He 4 соответственно равны: 8,03; 7,68 и 7,07 МэВ на нуклон.

Решение. При образовании ядра 10 Ne 20 из свободных нуклонов выделилась бы энергия:

W Ne = W c у ·А = 8,03 20 = 160,6 МэВ.

Соответственно для ядра 6 12 С и двух ядер 2 4 He:

W с = 7,68 ·12 = 92,16 МэВ,

W Не = 7,07· 8 = 56,56 МэВ.

Тогда при образовании 10 20 Ne из двух ядер 2 4 He и ядра 6 12 С выделилась бы энергия:

W = W Ne – W c – W He

W= 160,6 – 92,16 – 56,56 = 11,88 МэВ.

Такую же энергию необходимо затратить на процесс разделения ядра 10 20 Ne на 6 12 С и 2 2 4 H.

Ответ. E = 11,88 МэВ.

5 . Найти энергию связи ядра атома алюминия 13 Al 27 , найти удельную энергию связи.

Решение. Ядро 13 Al 27 состоит из Z=13 протонов и

A-Z = 27 - 13 нейтронов.

Масса ядра равна

m я = m ат - Z·m е = 27/6,02·10 26 -13·9,1·10 -31 = 4,484·10 -26 кг=

27,012 а.е.м.

Дефект массы ядра равен ∆m = Z·m p +(A-Z)·m n - m я

Численное значение

∆m = 13·1,00759 + 14×1,00899 - 26,99010 = 0,23443 а.е.м.

Энергия связи W св = 931,5·∆m = 931,5·0,23443 = 218,37 МэВ

Удельная энергия связи W уд = 218,37/27 = 8,08МэВ/нуклон.

Ответ: энергия связи W св = 218,37 МэВ; удельная энергия связи W уд = 8,08 МэВ/нуклон.

16. Ядерные реакции

Ядерными реакциями называют процессы превращения атомных ядер, вызванные их взаимодействием друг с другом или с элементарными частицами.

При записи ядерной реакции слева пишется сумма исходных частиц, затем ставится стрелка, а за ней сумма конечных продуктов. Например,

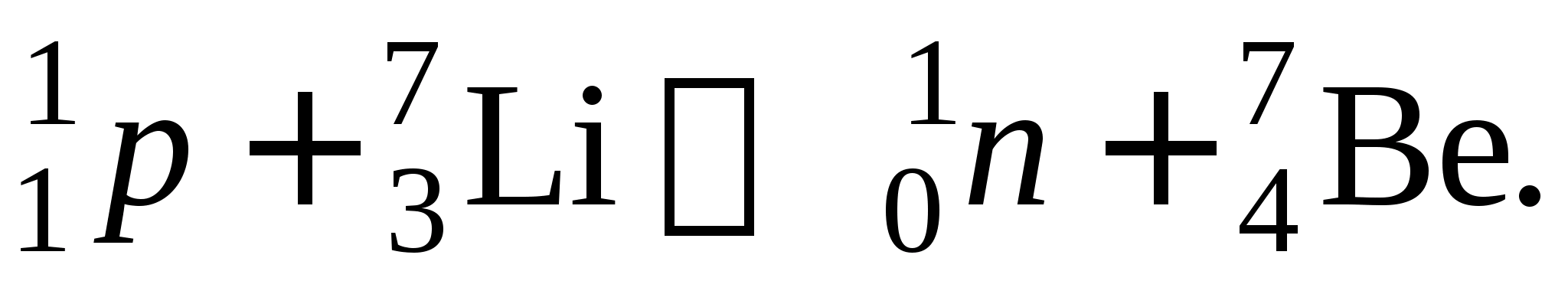
Эту же реакцию можно записать в более короткой символической форме

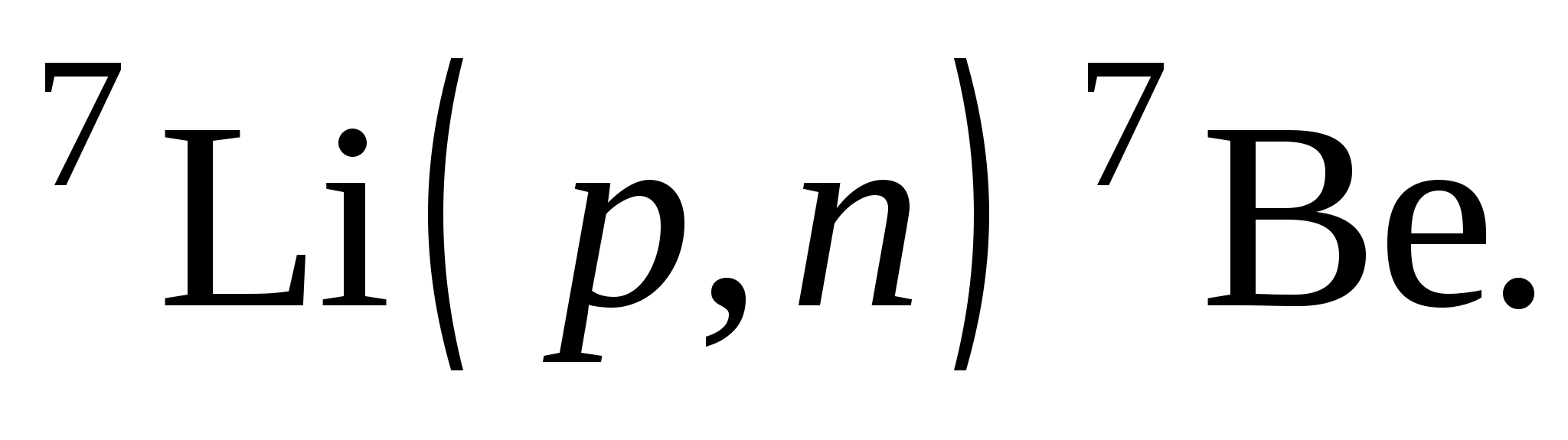
При рассмотрении ядерных реакций используются точные законы сохранения: энергии, импульса, момента импульса, электрического заряда и другие. Если в качестве элементарных частиц в ядерной реакции фигурируют только нейтроны, протоны и γ – кванты, то в процессе реакции сохраняется и число нуклонов. Тогда должны соблюдаться баланс нейтронов и баланс протонов в начальном и конечном состояниях. Для реакции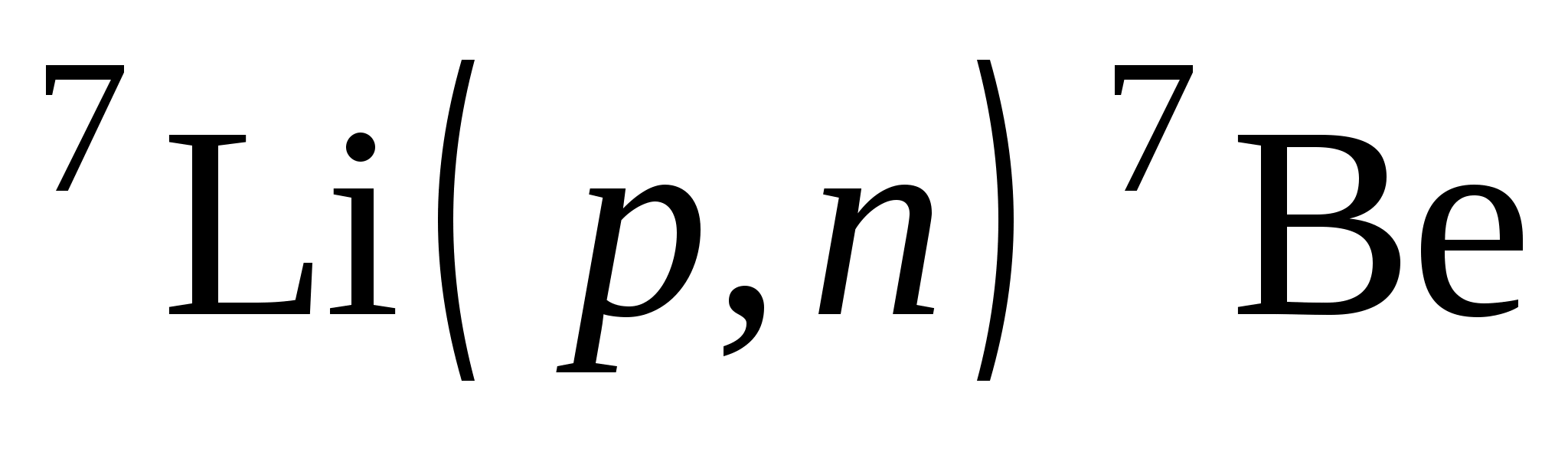

получим:

Число протонов 3 + 1 = 0 + 4;

Число нейтронов 4 + 0 = 1 + 3.

Пользуясь этим правилом можно идентифицировать одного из участников реакции, зная остальных. Достаточно частыми участниками ядерных реакций являются α – частицы (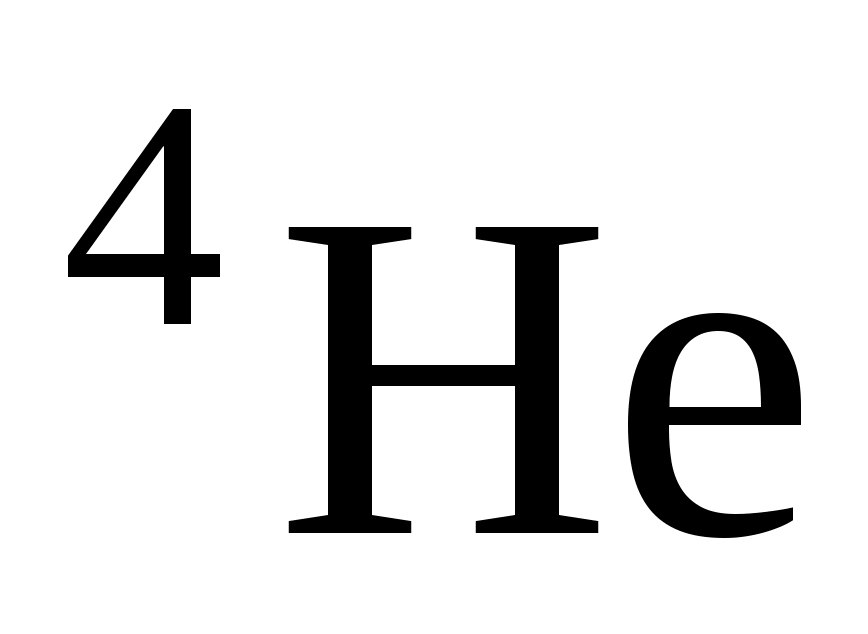

- ядра гелия), дейтроны (

- ядра тяжелого изотопа водорода, содержащие кроме протона по одному нейтрону) и тритоны (

- ядра сверхтяжелого изотопа водорода, содержащие кроме протона два нейтрона).

Разность энергий покоя начальных и конечных частиц определяет энергию реакции. Она может быть как больше нуля, так и меньше нуля. В более полной форме рассмотренная выше реакция записывается так:

где Q – энергия реакции. Для ее расчета с помощью таблиц свойств ядер сравнивают разность суммарной массы исходных участников реакции и суммарной массы продуктов реакции. Затем полученная разность масс (обычно выраженную в а.е.м.) пересчитывается в энергетические единицы (1 а.е.м. соответствует 931,5 МэВ).

17. Примеры решения задач

1. Определить неизвестный элемент, образующийся при бомбардировке ядер изотопов алюминия 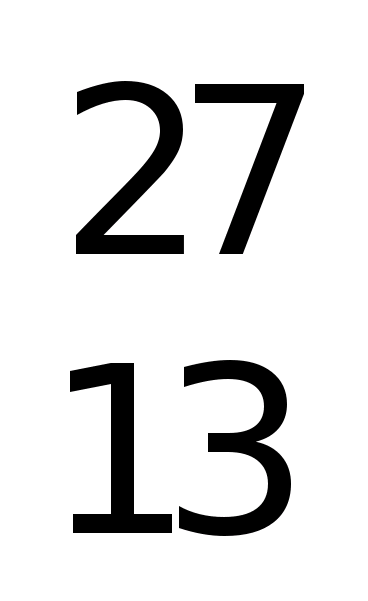Аl -частицами, если известно, что один из продуктов реакции нейтрон.

Решение. Запишем ядерную реакцию:

Al + 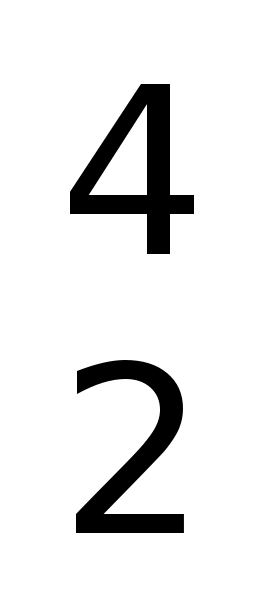

X + n.

По закону сохранения массовых чисел: 27+4 = А+1 . Отсюда массовое число неизвестного элемента А = 30 . Аналогично по закону сохранения зарядов 13+2 = Z+0 и Z = 15.

Из таблицы Менделеева находим, что это изотоп фосфора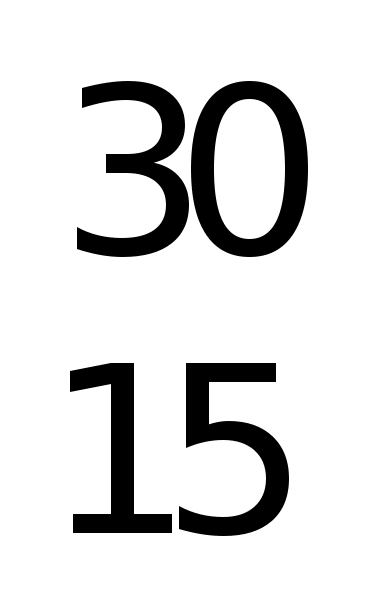Р .

2. Какая ядерная реакция записана уравнением

?

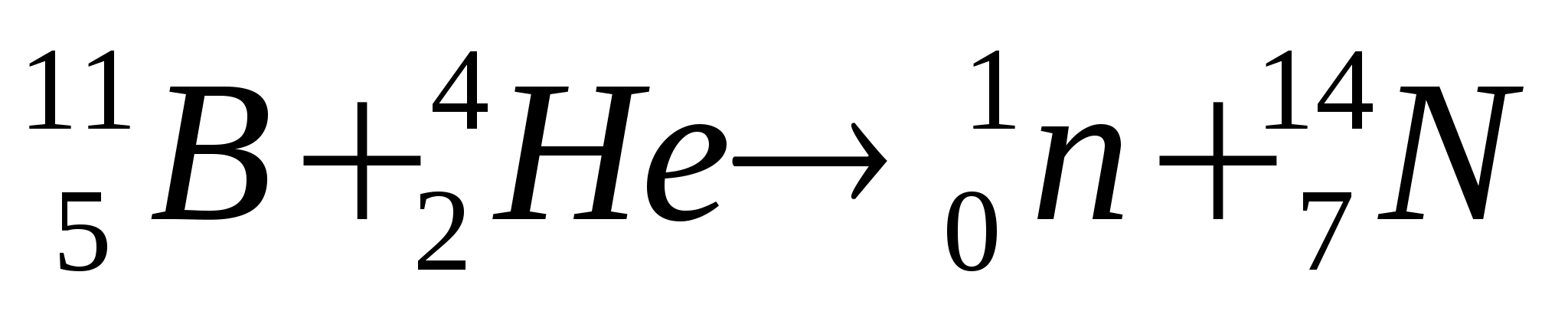Решение. Числа, стоящие около символа химического элемента означают: внизу – номер данного химического элемента в таблице Д.И.Менделеева (или заряд данной частицы), а вверху – массовое число, т.е. количество нуклонов в ядре (протонов и нейтронов вместе). По таблице Менделеева замечаем, что на пятом месте находится элемент бор В, на втором – гелий Не, на седьмом =- азот N. Частица 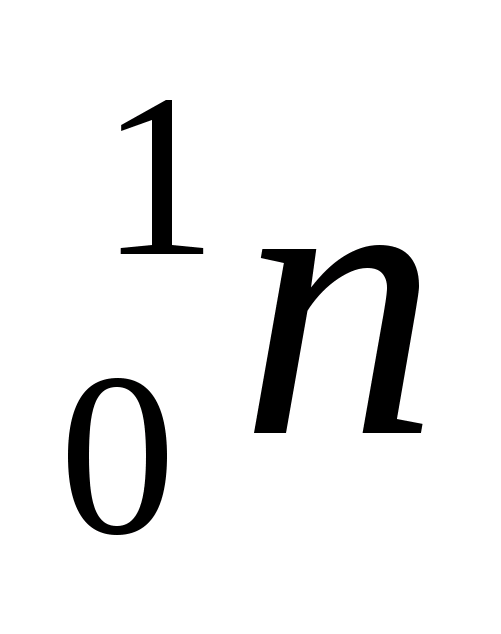- нейтрон. Значит, реакцию можно прочитать так: ядро атома бора с массовым числом 11 (бор-11) после захвата

- частицы (одно ядро атома гелия) выбрасывает нейтрон и превращается в ядро атома азота с массовым числом 14 (азот-14).

3. При облучении ядер алюминия – 27 жесткими 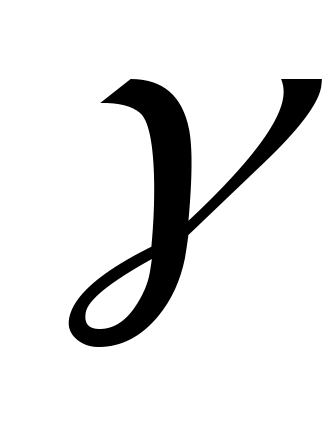– квантами образуются ядра магния – 26. Какая частица выделяется в этой реакции? Написать уравнение ядерной реакции.

Решение.

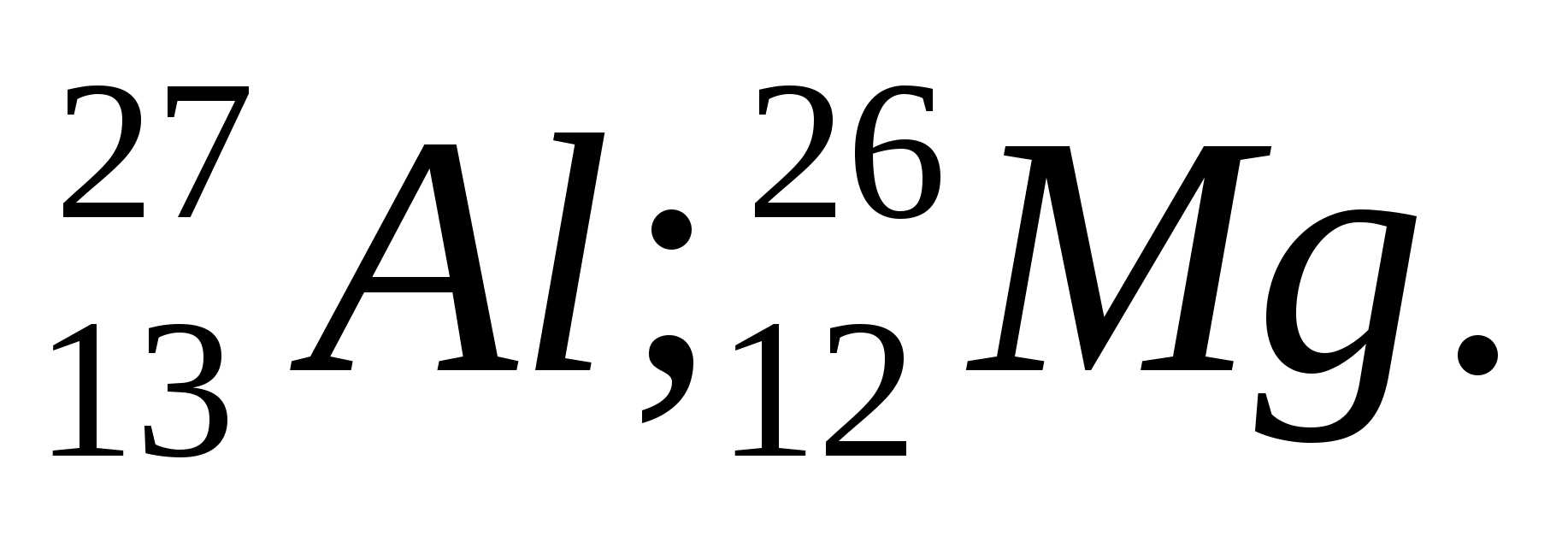
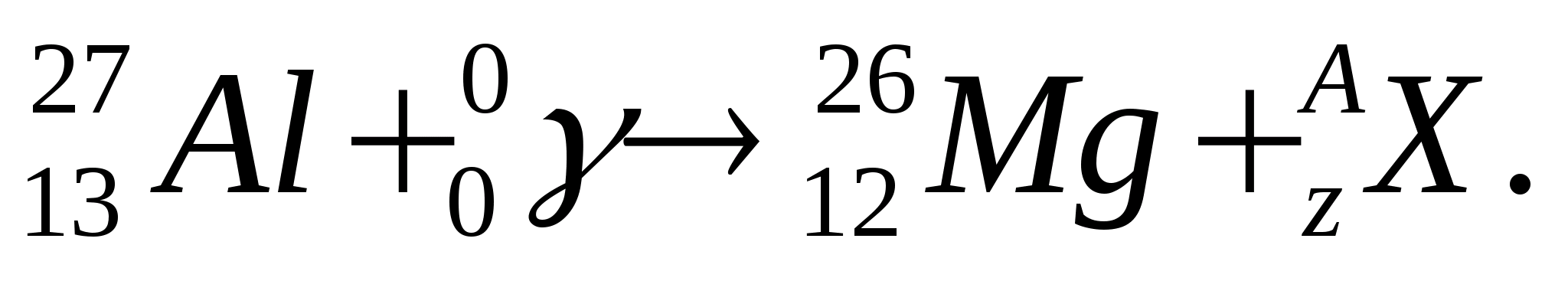
По закону сохранения заряда: 13+0=12+Z;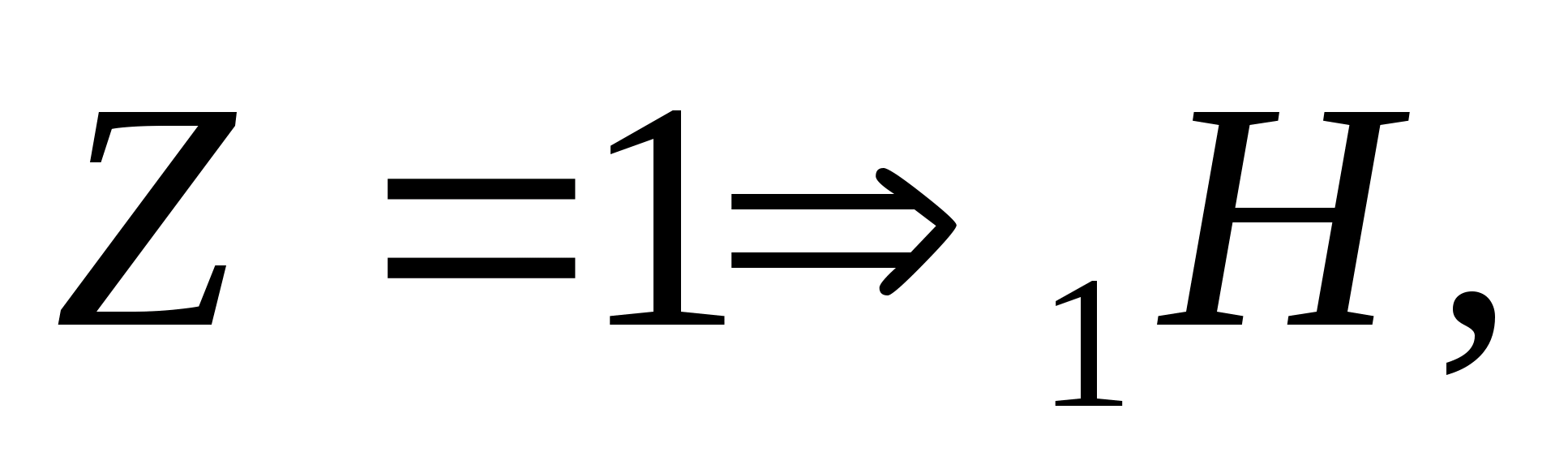

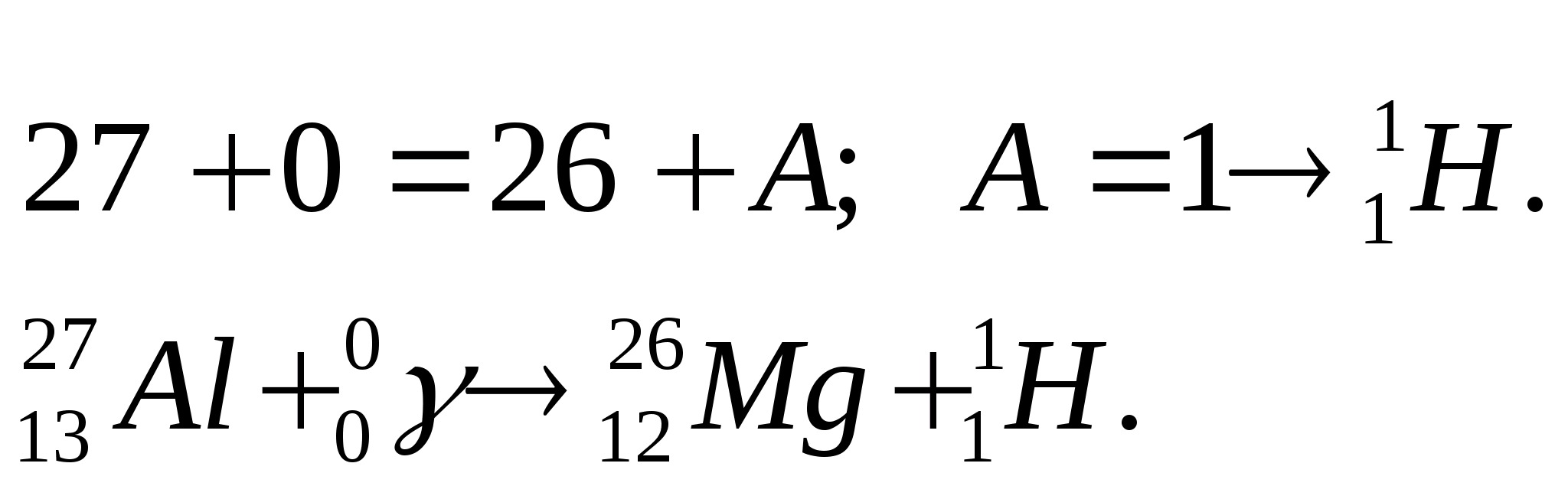
4. При облучении ядер некоторого химического элемента протонами образуются ядра натрия – 22 и - частицы (по одной на каждый акт превращения). Какие ядра облучались? Написать уравнение ядерной реакции.

Решение. По периодической системе химических элементов Д.И.Менделеева: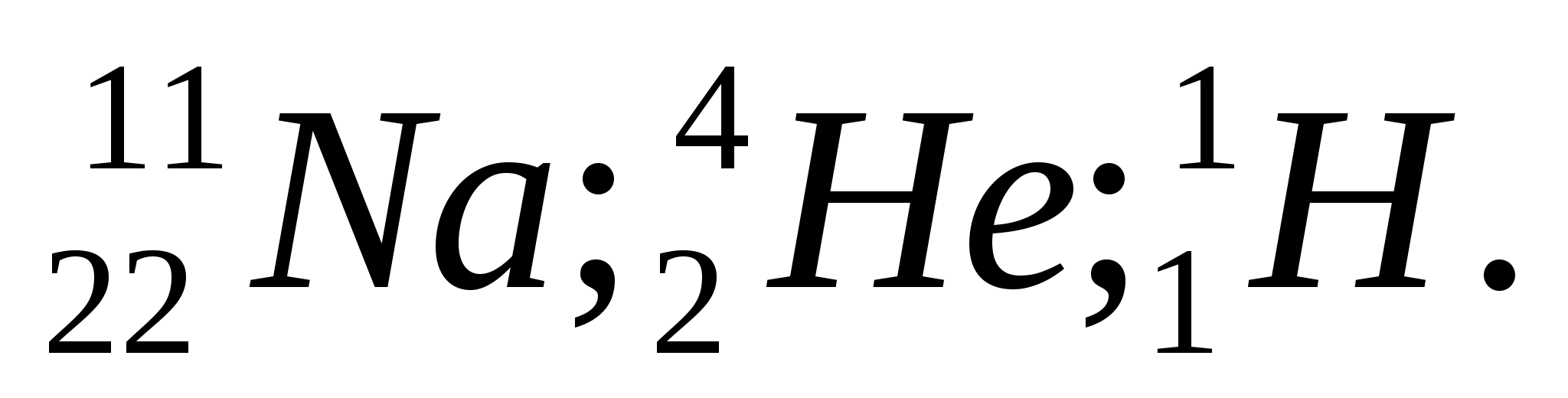

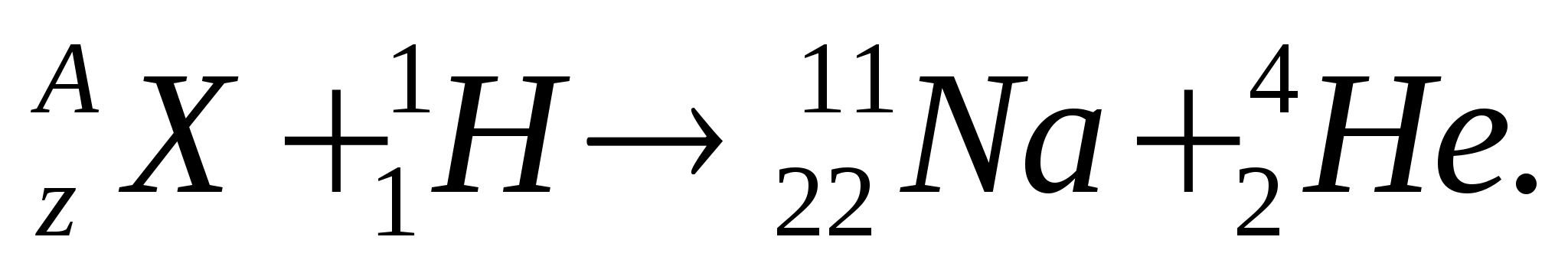
По закону сохранения заряда:

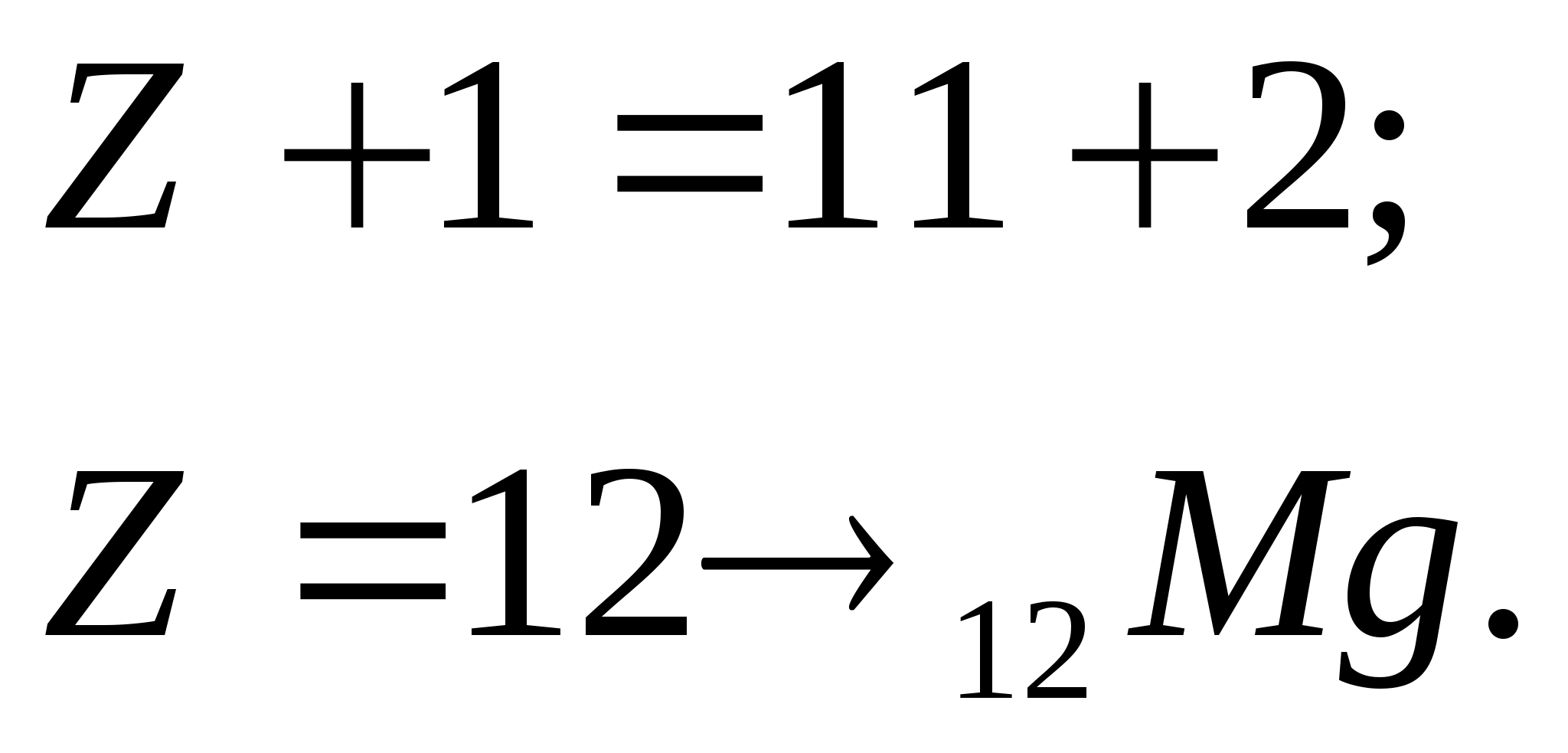
По закону сохранения массового числа:

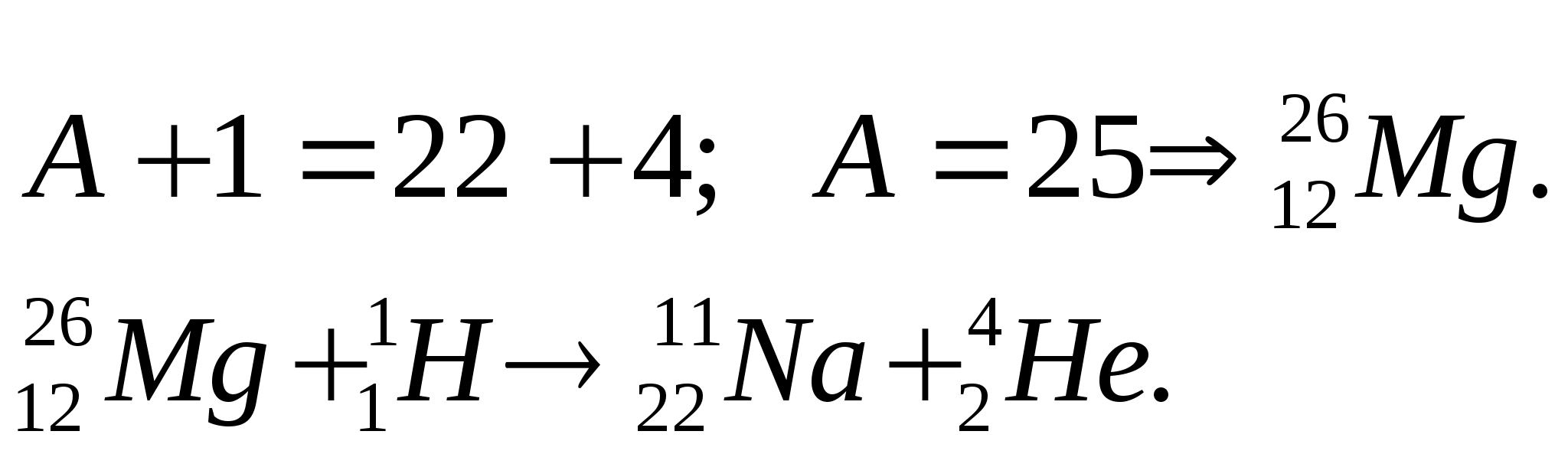
5 . При бомбардировке изотопа азота 7 N 14 нейтронами получается изотоп углерода 6 C 14 , который оказывается β-радиоактивным. Написать уравнения обеих реакций.

Решение . 7 N 14 + 0 n 1 → 6 C 14 + 1 H 1 ; 6 C 14 → -1 e 0 + 7 N 14 .

6. Стабильным продуктом распада 40 Zr 97 является 42 Mo 97 . В результате каких радиоактивных превращений 40 Zr 97 он образуется?

Решение. Запишем две реакции β-распада, происходящие последовательно:

1) 40 Zr 97 →β→ 41 X 97 + -1 e 0 , X ≡ 41 Nb 97 (ниобий),

2) 41 Nb 97 →β→ 42 Y 97 + -1 e 0 , Y ≡ 42 Mo 97 (молибден).

Ответ : в результате двух β-распадов из атома циркония образуется атом молибдена.

18. Энергия ядерной реакции

Энергия ядерной реакции (или тепловой эффект реакции)

где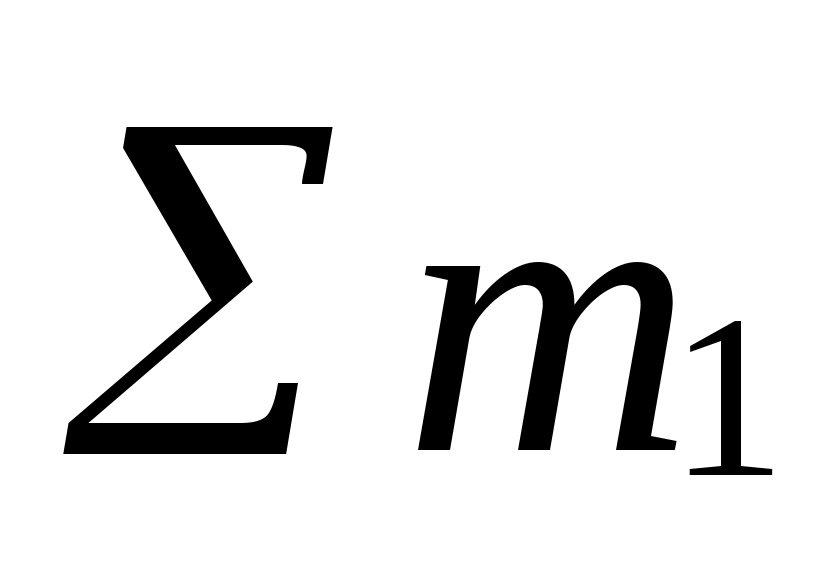

- сумма масс частиц до реакции,

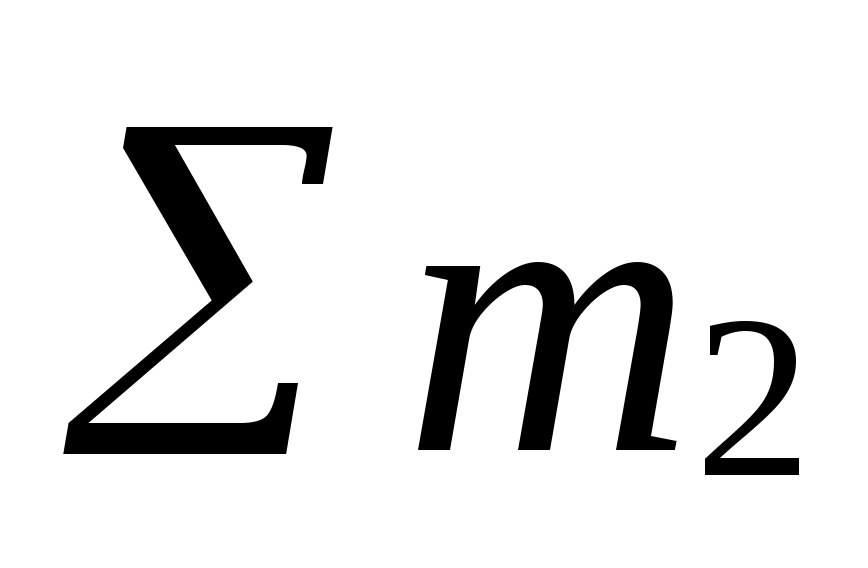- сумма масс частиц после реакции.

Если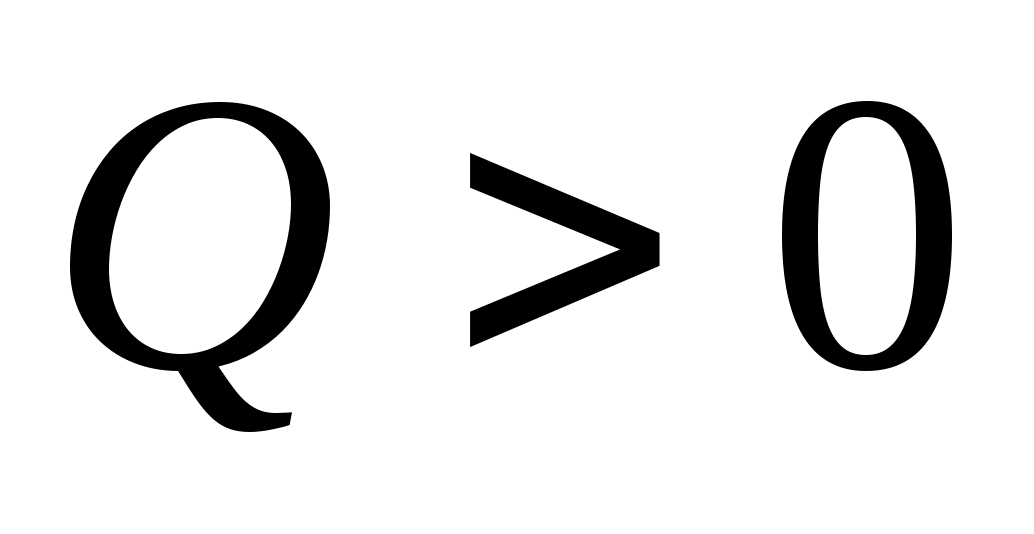

, реакция называется экзоэнергетической, так как идет с выделением энергии. При Q < 0 реакция называется эндоэнергетической и для ее возбуждения необходимо затратить энергию (например, ускорить частицы, т.е. сообщить им достаточную кинетическую энергию).

Деление ядра нейтронами – экзоэнергетическая реакция , при которой ядро, захватывая нейтрон, расщепляется на два (изредка – на три) большей частью неравных радиоактивных осколка, испуская вместе с этим гамма – кванты и 2 – 3 нейтрона. Эти нейтроны, при наличии вокруг достаточного количества делящегося вещества, могут, в свою очередь, вызывать деление окружающих ядер. В этом случае возникает цепная реакция, сопровождающаяся выделением большого количества энергии. Энергия выделяется за счет того, что делящееся ядро обладает или очень малым дефектом массы, или даже избытком массы вместо дефекта, что и является причиной неустойчивости таких ядер по отношению к делению.

энергия выделяется,

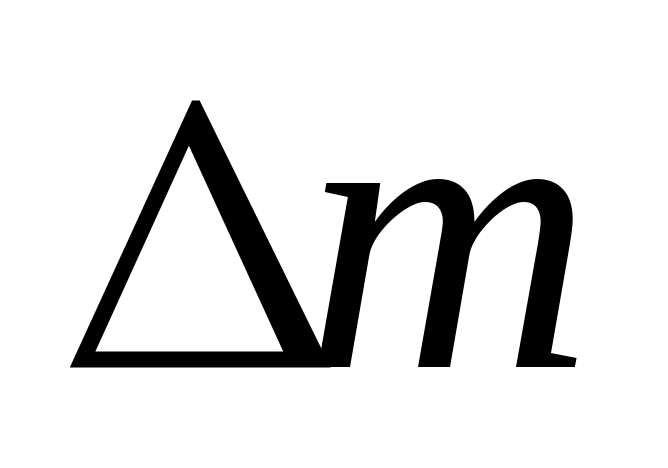=- 0,00352 а.е.м.

3. При делении ядра урана – 235 в результате захвата медленного нейтрона образуются осколки: ксенон – 139 и стронций – 94. Одновременно выделяются три нейтрона. Найти энергию, освобождающуюся при одном акте деления.

Решение. Очевидно, что при делении сумма атомных масс результирующих частиц меньше суммы масс исходных частиц на величину

Предполагая, что вся освобождающаяся при делении энергия переходит в кинетическую энергию осколков, получаем после подстановки числовых значений:

4. Какое количество энергии выделяется в результате термоядерной реакции синтеза 1 г гелия из дейтерия и трития?

реакцией деления тяжелых ядер , например

В этой реакции наблюдается размножение нейтронов. Важнейшей величиной является коэффициент размножения нейтронов k . Он равен отношению общего числа нейтронов в каком-либо поколении к породившему их общему числу нейтронов в предыдущем поколении. Таким образом, если в первом поколении было N 1 нейтронов, то их число в n-м поколении будет

N n = N 1 k n .

При k =1 реакция деления стационарна, т.е. число нейтронов во всех поколениях одинаково – размножения нейтронов нет. Соответствующее состояние реактора называется критическим.

При k >1 возможно образование цепной неуправляемой лавинообразной реакции, что и происходит в атомных бомбах. В атомных станциях поддерживается управляемая реакция, в которой за счет графитовых поглотителей число нейтронов поддерживается на некотором постоянном уровне.

Возможны ядерные реакции синтеза или термоядерные реакции, когда из двух легких ядер образуется одно более тяжелое ядро. Например, синтез ядер изотопов водорода – дейтерия и трития и образование ядра гелия:

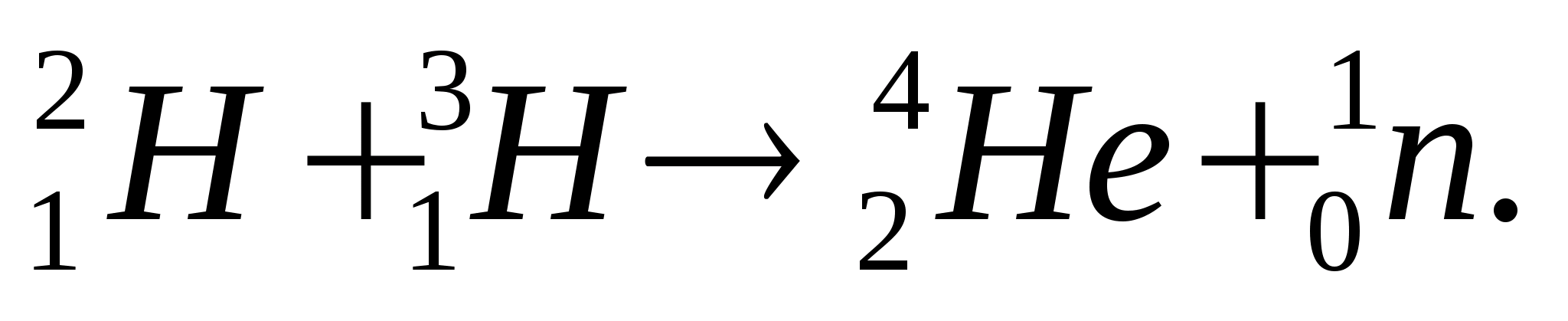
При этом выделяется 17,6 МэВ энергии, что примерно в четыре раза больше из расчета на один нуклон, чем в ядерной реакции деления. Реакция синтеза протекает при взрывах водородных бомб. Более 40 лет ученые работают над осуществлением управляемой термоядерной реакции, которая открыла бы доступ человечеству к неисчерпаемой “кладовой” ядерной энергии.

21. Биологическое действие радиоактивных излучении

Излучения радиоактивных веществ оказывают очень сильное воздействие на все живые организмы. Даже сравнительно слабое излучение, которое при полном поглощении повышает температуру тела лишь на 0,00 1 °С, нарушает жизнедеятельность клеток.

Живая клетка - это сложный механизм, не способный продолжать нормальную деятельность даже при малых повреждениях отдельных его участков. Между тем даже слабые излучения способны нанести клеткам существенные повреждения и вызвать опасные заболевания (лучевая болезнь). При большой интенсивности излучения живые организмы погибают. Опасность излучений усугубляется тем, что они не вызывают никаких болевых ощущений даже при смертельных дозах.

Механизм поражающего биологические объекты действия излучения еще недостаточно изучен. Но ясно, что оно сводится к ионизации атомов и молекул и это приводит к изменению их химической активности. Наиболее чувствительны к излучениям ядра клеток, особенно клеток, которые быстро делятся. Поэтому в первую очередь излучения поражают костный мозг, из-за чего нарушается процесс образования крови. Далее наступает поражение клеток пищеварительного тракта и других органов.

Сильное влияние оказывает облучение на наследственность. В большинстве случаев это влияние является неблагоприятным.

Облучение живых организмов может оказывать и определенную пользу. Быстро размножающиеся клетки в злокачественных (раковых) опухолях более чувствительны к облучению, чем нормальные. На этом основано подавление раковой опухоли -лучами радиоактивных препаратов, которые для этой цели более эффективны, чем рентгеновские лучи.

Энергия связи E св ядра (A,Z) - выраженная в энергетических единицах разность между массой M(A,Z) ядра и суммой масс (A- Z) нейтронов и Zпротонов:

E св (A, Z) = [(A - Z)M n + ZM p ) - M(A,Z) ]c 2 .

Энергия связи ядра E св определяет минимальную энергию, которую надо затратить, чтобы разделить ядро на отдельные нуклоны.
Исходя из аналогии между заряженной жидкой каплей радиуса R= R 0 A 1/3 (где R 0 = 1.3 Фм ) и атомным ядром, К.Вайцзеккер в 1935 г. написал полуэмпирическую формулу для энергии связи ядра:

Значения коэффициентов a 1 - a 5 были подобраны так, чтобы наилучшим образом воспроизвести экспериментальные значения масс стабильных ядер:
a 1 = 15.6 МэВ, a 2 = 17.2 МэВ, a 3 = 0.72 МэВ, a 4 = 23.6 МэВ,

Энергия связи E св (A,Z) растет с ростом массового числа A, достигая величины
~ 2 ГэВ в области массовых чисел A~ 270. Поэтому гораздо более удобно использовать удельную энергию связи
ε = E св /A- энергию связи, приходящуюся на один нуклон (Рис. 2). Величина удельной энергии связи для большинства ядер ~ 8 МэB. Пропорциональность полной энергии связи числу нуклонов в ядре объясняется тем, что ядерные силы – короткодействующие, обладают свойством насыщения.
В рамках капельной модели ядра удалось объяснить многие свойства атомных ядер и получить полуэмпирическую формулу для энергии связи атомных ядер, которая позволила понять некоторые закономерности α- и β-распадов, процессов деления ядер и оценивать массы и энергии связи ядер.

Радиоактивностью называется способность атомного ядра самопроизвольно распадаться с испусканием частиц.
Радиоактивный распад ядра возможен тогда, когда он энергетически выгоден, т.е. сопровождается выделением энергии. Условием этого является превышение массы M исходного ядра суммы масс m i продуктов распада, которому соответствует неравенство M > ∑m i . Это условие является необходимым, но не всегда достаточным. Распад может быть запрещен другими законами сохранения – сохранения момента количества движения, электрического заряда, барионного заряда и т.д.
Радиоактивный распад характеризуется временем жизни радиоактивного изотопа, типом испускаемых частиц, их энергиями.
Основными видами радиоактивного распада являются:

• α-распад – испускание атомными ядрами α-частиц;
• β-распад – испускание атомными ядрами электрона и антинейтрино, позитрона и нейтрино, поглощение ядром атомного электрона с испусканием нейтрино;
• γ-распад – испускание атомными ядрами γ-квантов;
• спонтанное деление – распад атомного ядра на два осколка сравнимой массы.

К более редким видам радиоактивного распада относятся процессы испускания ядрами двух электронов, одного или двух протонов, а также кластеров – лёгких ядер от 12 C до 32 S. Во всех видах радиоактивности (кроме γ-распада) изменяется состав ядра – число протонов Z, массовое число Aили и то и другое одновременно.
На характеристики радиоактивного распада оказывает существенное влияние тип взаимодействия, вызывающего распад ядра. Так, α-распад вызывается сильным взаимодействием, β-распад - слабым, а γ-распад - электромагнитным.
Радиоактивный распад – статистический процесс. Каждое радиоактивное ядро может распасться в любой момент, и закономерности распада атомного ядра наблюдаются только в среднем, в случае распада достаточно большого количества ядер.
Для характеристики скорости (вероятности) радиоактивного распада используются три взаимосвязанные величины - постоянная распада λ, среднее время жизни tи период полураспада T 1/2 .
Постоянная распада λ - вероятность распада ядра в единицу времени. Если в образце в момент времени t имеется N радиоактивных ядер, то количество ядер dN, распавшихся за время dt, пропорционально N, λ и интервалу времени dt:

Закон радиоактивного распада имеет вид:

N(t)= N 0 e -λt ,

где N 0 – количество радиоактивных ядер в исходный момент времени t = 0.

Среднее время жизни τ:

.

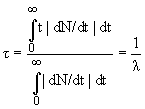Период полураспада T 1/2 – время, за которое первоначальное количество радиоактивных ядер уменьшается в два раза:

T 1/2 = ln2/λ=0.693/λ = τln2.

Размеры и форма ядра. Впервые размеры ядра правильно оценил Резерфорд, использовав для этой цели рассеяние альфа-частиц. Его первые эксперименты показали, что размеры заряженной части ядра – порядка 10 –14 м. Более поздние и более точные эксперименты позволили установить, что радиус ядра приблизительно пропорционален А 1/3 и, следовательно, плотность ядерного вещества почти постоянна. (Она колоссальна: 100 000 т/мм 3 .)

С открытием нейтрона стало ясно, что он представляет собой идеальное средство исследования ядра, поскольку нейтральные частицы, проходя на значительном удалении от ядра, не испытывают отклонения под действием заряда ядра. Другими словами, нейтрон сталкивается с ядром, если расстояние между их центрами оказывается меньше суммы их радиусов, а в противном случае не отклоняется. Опыты по рассеянию пучка нейтронов показали, что радиус ядра (в предположении сферической формы) равен:

R = r 0 A 1/3 ,

r 0 » 1,4×10 –15 м.

Таким образом, радиус ядра урана-238 равен 8,5×10 –15 м. Полученное значение соответствует радиусу действия ядерных сил; оно характеризует расстояние от центра ядра, на котором внешний нейтральный нуклон начинает впервые «ощущать» его воздействие. Такая величина радиуса ядра сравнима с расстоянием от центра ядер, на котором происходит рассеяние альфа-частиц и протонов.

Рассеяние альфа-частиц, протонов и нейтронов на ядрах обусловлено действием ядерных сил; следовательно, такие измерения радиусов ядер дают оценку радиуса действия ядерных сил. Взаимодействие же электронов с ядрами почти полностью определяется электрическими силами. Поэтому рассеяние электронов можно использовать для изучения формы распределения заряда в ядре. Эксперименты с электронами очень высоких энергий, проведенные Р.Хофстедтером в Станфордском университете, дали детальную информацию о распределении положительного заряда по радиусу ядра. На рис. 6 представлено угловое распределение рассеянных ядрами золота электронов с энергией 154 МэВ. Верхняя кривая характеризует угловое распределение, рассчитанное в предположении, что положительный заряд сконцентрирован в точке; очевидно, что экспериментальные данные этому предположению не соответствуют. Гораздо лучшее согласие достигается в предположении о равномерном распределении протонов по объему ядра (нижняя кривая). Однако «радиус заряда» оказывается примерно на 20% меньше радиуса «ядерных сил», полученного на основе данных по рассеянию нейтронов. Это может означать, что распределение протонов в ядре отличается от распределения нейтронов.

Нуклоны в ядрах находятся в состояниях существенно отличающихся от их свободных состояний. Между ними существует особое ядерное (или сильное) взаимодействие - притяжение. Это взаимодействие обуславливает устойчивость ядер, несмотря на электростатическое отталкивание протонов.

Масса ядра всегда меньше суммы масс входящих в него нуклонов. Причина этого заключается в том, что при объединении нуклонов в ядро выделяется энергия связи нуклонов друг с другом.

Энергия связи равна работе, которую нужно совершить, чтобы расщепить ядро на составляющие его нуклоны без придания им кинетической энергии.

Энергия связи находится по формуле:

В этом выражении величина называется дефектом масс, она равна разности между суммарной массой всех нуклонов и массой ядра:

При практических расчетах вместо масс ядер пользуются массами атомов и энергию связи вычисляют по формуле:

Для расчета энергии связи поступают следующим образом:

§ В справочнике находят значения масс в атомныхединицах массы (а.е.м.)

§ Находят дефект масс по формуле:

§ Находят энергию связи в мегаэлектронвольтах (МэВ) по формуле: . (7)

Энергия связи, приходящая на один нуклон называется удельной энергией связи:

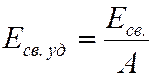. (8)

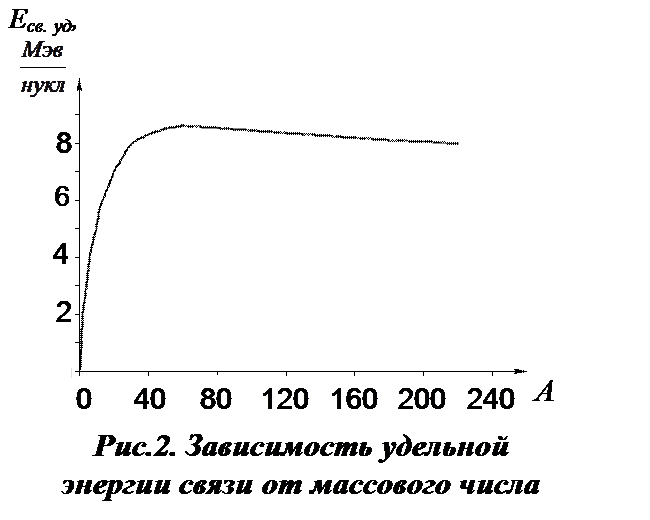Зависимость удельной энергии связи от массового числа имеет вид кривой с максимумом, приведённый на рисунке 2. Из этой зависимости следует, что максимальная удельная энергия связи приходится на массовые числа 50¸60 (т.е. для элементов от Сr до Zn). Она достигает 8,7 МэВ/нуклон. С ростом и уменьшением массового числа удельная энергия связи уменьшается. Такая зависимость делает энергетически возможным протекание двух видов процессов.

1. Деление тяжелых ядер на более лёгкие.

Расчёт показывает, что деление ядра с массовым числом А=240 (Е св. уд = 7,5 МэВ) на два ядра с массовыми числами А=120 (Е св. уд = 8,5 МэВ) привело бы к высвобождению энергии, равной

DЕ = (2 × 120 × 8,5 – 240 × 7,5) = 240 МэВ

2. Слияние (синтез) легких ядер в одно более тяжёлое ядро.

Например, слияние двух ядер тяжелого водорода в ядро гелия привело бы к выделению энергии 24 МэВ .

Для сравнения: при реакции С + О 2 ® СО 2 (сгорание угля) выделяется энергия » 5 эВ.

Итак, ядра со значениями А=50÷60 являются наиболее устойчивыми.

Почему же другие ядра также стабильны? Причина заключается в следующем. Для деления тяжёлого ядра на более легкие он должно пройти несколько промежуточных состояний. Их энергия превышает энергию основного состояния ядра. Поэтому для процесса деления ядра требуется дополнительная энергия (энергия активации). В обычных условиях ядра не получают эту энергию – спонтанного деления не происходит. Энергия активации может быть сообщена тяжёлому ядру путём захвата им нейтрона. Процесс деления ядер урана или плутония под действием нейтронов лежит в основе работы ядерного реактора и атомной бомбы.

Для слияния лёгких ядер в одно ядро они должны приблизиться друг к другу на расстояние ≈10 -15 м. Такому сближению препятствуют кулоновские силы отталкивания. Чтобы преодолеть это отталкивание, ядра должны двигаться с огромными скоростями, соответствующими температуре Т≈10 9 К.

Процесс синтеза лёгких ядер называется термоядерной реакцией. Такая реакция протекает в недрах звёзд и Солнца, а также при взрывах водородных бомб.

Если вы купите 5 яблок по 200 г каждое, сложите их в пакет, а потом, взвесив его, увидите, что яблок у вас меньше 1 кг, вы, конечно, удиви-тесь, но не заподозрите «природу» в обмане. Вы решите, что вас обманул продавец, что яблоки, которые, как вам обеща-ли, весят по 200 г, на самом деле легче. Но если физик, изме-рив массу ядра, получит, что она меньше суммы масс соста-вляющих ядро нуклонов, он тоже не заподозрит «природу» в обмане, он даже не удивится. Он знает, что это связано с взаимодействием между частицами.

Энергия покоя составной системы равна сумме энергий по-коя составляющих ее частиц, их кинетической энергии и энергии взаимодействия. Кинетическая энергия составляю-щих систему частиц по величине меньше энергии их взаи-модействия (последняя отрицательна), иначе частицы раз-бежались бы далеко друг от друга. Поэтому энергия покоя составной системы меньше суммы энергий покоя составля-ющих ее частиц. А значит, в соответствии с формулой Эйн-штейна

E = mc 2

масса составной системы тоже меньше сум-мы масс составляющих ее частиц. Куда девается энергия при образовании связанной системы? Ответ по форме очень прост — она излучается. Но если бы мы захотели де-тально описать процесс излучения, нам пришлось бы обра-титься к сложным полевым теориям . Вернемся к нашим яб-локам. Почему же мы уверены, что масса пакета с яблоками должна равняться сумме масс всех яблок и, конечно, паке-та? Просто потому, что яблоки не образовали связанное со-стояние.

Масса ядра m меньше масс составляющих ядро нуклонов на величину Δm, называемую дефектом масс :

Δm = Zm p + Nm n — m ,

где m p и m n — массы протона и нейтрона.

Энергией связи E СВ ядра называют разность энергий покоя ядра и составляющих ядро нуклонов:

E СВ = Zm p c 2 + Nm n c 2 — mc 2 = Δmc 2 .

Именно такую энергию нужно за-тратить для того, чтобы расщепить ядро на отдельные ну-клоны. Для большинства ядер, кроме самых легких, энергия связи примерно пропорциональна числу нуклонов в ядре, а удельная энергия связи

ε СВ = E СВ / A

почти постоянна и соста-вляет ~6-8 МэВ/нуклон. Это свойство называют насыще-нием ядерных сил . Оно свидетельствует о том, что нуклон в ядре эффективно взаимодействует только с небольшим чис-лом других нуклонов. Если бы каждый нуклон взаимодейст-вовал со всеми нуклонами, то удельная энергия связи была бы пропорциональна числу нуклонов в ядре A.

Относительный ядерный дефект масс :

Δm / m = E СВ / m p c 2 .

Для большинства ядер он составляет ~0,65-0,85%, для лег-ких ядер он меньше, например, для дейтрона он — 0,1%. Материал с сайта

На этой странице материал по темам: