Как определяется длина волны де бройля. Элементы квантовой механики Корпускулярно-волновой дуализм свойств частиц вещества

В 1924г. Луи де Бройль (французский физик) пришел к выводу, что двойственность света должна быть распространена и на частицы вещества - электроны. Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.

Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

- волна де Бройля

p =mv - импульс частицы, h - постоянная Планка.

Волны де Бройля , которые иногда называют электронными волнами, не являются электромагнитными.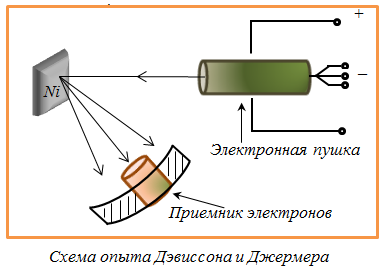

В 1927 году Дэвиссон и Джермер (амер. физик) подтвердили гипотезу де Бройля обнаружив дифракцию электронов на кристалле никеля. Дифракционные максимумы соответствовали формуле Вульфа - Брэггов 2dsin   n , а брэгговская длина волны оказалась в точности равной .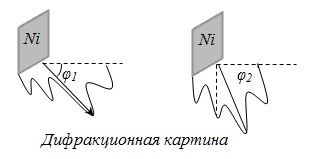

Дальнейшее подтверждение гипотезы де Бройля в опытах Л.С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (Е  50 кэВ) через фольгу из различных металлов. Затем была обнаружена дифракция нейтронов, протонов, атомных пучков и молекулярных пучков. Появились новые методы исследования вещества - нейтронография и электронография и возникла электронная оптика.

Макротела также должны обладать всеми свойствами (m = 1кг, следовательно,   ·  м - невозможно обнаружить современными методами - поэтому макротела рассматриваются только как корпускулы).

§2 Свойства волн де Бройля

Пусть частица массы m движется со скоростью v . Тогда фазовая скорость волн де Бройля

Т.к. c > v, то фазовая скорость волн де Бройля больше скорости света в вакууме (v ф может быть больше и может быть менше с, в отличие от групповой).

Групповая скорость

следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

Для фотона

т.е. групповая скорость равная скорости света.

§3 Соотношение неопределенностей Гейзенберга

Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р . Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.

Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к. . Только рассматривая протяженный участок мы сможем определить импульс частицы. Чем больше , тем точнее р и наоборот, чем меньше , тем больше неопределенность в нахождении р .

Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.

Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h

(иногда записывают )

Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.

Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

следовательно, чем больше m, тем меньше неопределенности в определении координаты и скорости. При m = 10 -12 кг, ? = 10 -6 и Δx = 1% ?, Δv = 6,62·10 -14 м/с, т.е. не будет сказываться при всех скоростях, с которыми пылинки могут двигаться, т.е. для макротел их волновые свойства не играют никакой роли.

Пусть электрон движется в атоме водорода. Допустим Δx  -10 м (порядка размеров атома, т.е. электрон принадлежит данному атому). Тогда

Δv = 7,27·  м/с. По классической механике при движении по радиусу r  ,·  м v = 2,3·10 -6 м/с. Т.е. неопределенность скорости на порядок больше величины скорости, следовательно, нельзя применять законы классической механики к микромиру.

Из соотношения следует, что система имеющая время жизниt , не может быть охарактеризована определенным значением энергии. Разброс энергии возрастает с уменьшением среднего времени жизни. Следовательно, частота излученного фотона также должна иметь неопределенность =  h , т.е. спектральные линии будут иметь некоторую ширину  h , будут размыты. Измерив ширину спектральной линии можно оценить порядок времени существования атома в возбужденном состоянии.

ЭЛЕКТРОННАЯ ОПТИКА

Мы уже говорили о том, что свет обладает корпускулярно – волновым дуализмом: в некоторых явлениях ведет себя как волна (интерференция, дифракция, поляризация), в других (фотоэффект, поглощение света и др.) – как частица. Частица света – частица электромагнитного излучения оптического диапазона, имеющая энергию

и импульс

,

.

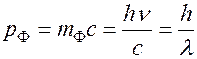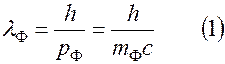Масса покоя фотона , т.е. фотон существует только тогда, когда он движется.

В 1924 году Луи де Бройль высказал предположение, что корпускулярно – волновой дуализм, возможно, проявляют и частицы вещества, в частности электроны. Это значит, что элементарную частицу можно охарактеризовать, сопоставляя частице некоторую волну, длина которой

.

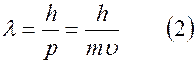Различие между формулами (1) и (2) существенно и заключается в том, что

1) у фотона нет инертной массы покоя, электроны же имеют массу покоя, а масса движущегося электрона

,

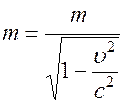2) у фотонов скорость их движения в вакууме является постоянной величиной, тогда как у электронов скорость движения может быть различной.

Длина волны

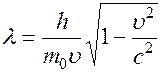
называется длиной волны де Бройля. Волна де Бройля не представляет собой какой – либо самостоятельный колебательный процесс, а только характеризует волновые свойства частицы.

Когда де Бройль опубликовал эту гипотезу, никаких экпериментальных доказательств её правильности не было. Только в 1927 году американские ученые Дэвиссон и Джермер подтвердили эту гипотезу опытом. Изучая рассеяние электронов на кристаллической структуре никеля, они случайно обнаружили дифракцию электронов. В этом же году Томсон и Тарковский уже специально изучали дифракцию электронов на металлической фольге.

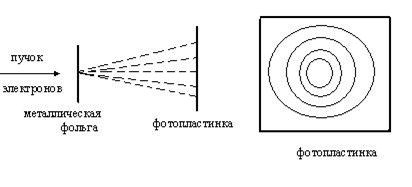
Пучок электронов, ускоренный напряжением порядка нескольких десятков киловольт, проходил через тонкую металлическую фольгу и попадал на фотопластинку. Оказалось, что электрон, попадая на фотопластинку, оказывает на неё такое же действие, как и фотон. Затем взяли золотую фольгу, опыт повторили - эффект оказался таким же. Отдельный электрон, пройдя фольгу (или кристалл) не дает наблюдаемой картины. Только в том случае, если через фольгу проходит много электронов, получается дифракционная картина (подобно дифракционной картине от света при наложении вторичных волн).

Позже была осуществлена дифракция нейтронов и других микрочастиц, что доказывает правоту идеи де Бройля о том, что микрочастицы вещества обладают волновыми свойствами.

Волна де Бройля очень мала. Например, для электрона, масса которого , движущегося со скоростью , длина волны . А для частицы с массой , движущейся со скоростью порядка , длина волны около .

Волновые свойства частиц используются в медицине для дифракционного структурного анализа, в основу которого положена формула Вульфа-Брэггов: , которую мы уже обсуждали. Дифракционно-структурный анализ применяется для определения упорядоченного или разупорядоченного расположения атомов и молекул вещества и для определения параметров кристаллической решетки.

И, конечно, нам интересно понимать принцип действия электронного микроскопа, в основе работы которого лежат волновые свойства электронов.

ВОЛНЫ ДЕ БРОЙЛЯ - волны, связанные с любой движущейся микрочастицей, отражающие квантовую природу микрочастиц.

Впервые квантовые свойства были открыты у эл--магн. поля. После исследования M. Плавком (M. Planck) законов теплового тел (1900) в науку вошло представление о "световых порциях" - квантах эл--магн. поля. Эти кванты - фотоны-во многом похожи на частицы (корпускулы): они обладают определёнными энергией и импульсом, взаимодействуют с веществом как целое. В то же время давно известны волновые свойства эл--магн. излучения, к-рые проявляются, напр., в явлениях и интерференции света. T. о., можно говорить о двойственной природе, или о корпускулярно-волновом дуализме, фотона.

В 1924 Л. де Бройль (L. de Broglie) высказал гипотезу о том, что корпускулярно-волновой дуализм присущ всем без исключения видам материи - электронам, протонам, атомам и т. д., причём количественные соотношения между волновыми и корпускулярными свойствами частиц те же, что и установленные ранее для фотонов. А именно, если частица имеет энергию и импульс, абс. значение к-рого равно р , то с ней связана волна частоты и длины , где6*10 -27 эрг*с - постоянная Планка. Эти волны и получили назв. В. де Б.

Для частиц не очень высокой энергии , где - масса и скорость частицы. Следовательно, длина В. де Б. тем меньше, чем больше масса частицы и её скорость. Напр., частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует В. де Б. с10 -18 , что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопич. тел. Для электронов с энергиями от 1 эВ до 10 000 эВ длины В. де Б. лежат в пределах от 10 до 0,1 , т. е. в интервале длин волн рентг. излучения. Поэтому волновые свойства электронов должны проявиться, напр., при их рассеянии на тех же кристаллах, на к-рых наблюдается дифракция рентгеновских лучей .

Первое эксперим. подтверждение гипотезы де Бройля получено в 1927 в опытах К. Дэвиссона (С. Davisson) и Л. Джермера (L. Germer). ускорялся в электрич. поле с разностью потенциалов 100-150 В (энергия таких электронов 100-150 эВ, что соответствует ) и падал на кристалл никеля, играющий роль пространственной дифракц. решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина к-рых определяется соотношением де Бройля. Волновые свойства электронов, нейтронов и др. частиц, а также атомов и молекул не только надёжно доказаны прямыми опытами, но и широко используются в установках с высокой разрешающей способностью, так что можно говорить об инженерном использовании В. де Б. (см. Дифракция частиц ).

Подтверждённая на опыте идея де Бройля о корпускулярно-волновом дуализме микрочастиц принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (по традиции за ними сохраняется термин "частицы") присущи и корпускулярные и волновые свойства, то, очевидно, любую из этих "частиц" нельзя считать ни частицей, ни волной в классич. понимании этих слов. Возникла потребность в такой теории, в к-рой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории - волновой, или квантовой, механики - и легла концепция де Бройля, уточнение к-рой привело к вероятностной интерпретации В. де Б. В 1926 M. Борн (M. Born) высказал идею о том, что волновым законам подчиняется величина, описывающая состояние частицы. Она была названа