Адиабатный процесс постоянная величина. Адиабатный процесс
Адиабатный процесс- это процесс без теплообмена с внешней средой. При адиабатном процессе энергообмен рабочего тела с окружающей средой происходит только в форме работы, энергообмена в форме теплоты нет. Эти условия выражаются соотношением: . Тогда уравнение первого закона термодинамики для адиабатного процесса имеет вид:
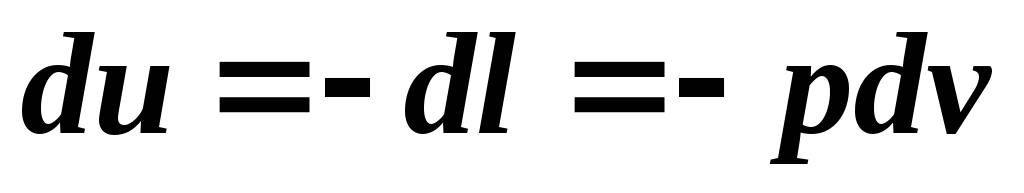 .
(5.4)
.
(5.4)
Из этого уравнения видно, что работа адиабатного процесса расширения совершается вследствие уменьшения внутренней энергии газа и, следовательно, температура газа уменьшается. Работа адиабатного сжатия полностью идет на увеличение внутренней энергии газа, то есть на повышение его температуры. Таким образом, изменение внутренней энергии и работа в адиабатном процессе эквивалентны по величине и противоположны по знаку.
Выведем уравнение адиабаты для идеального газа. Воспользуемся уравнением первого закона термодинамики:
Разделив переменные, получим:
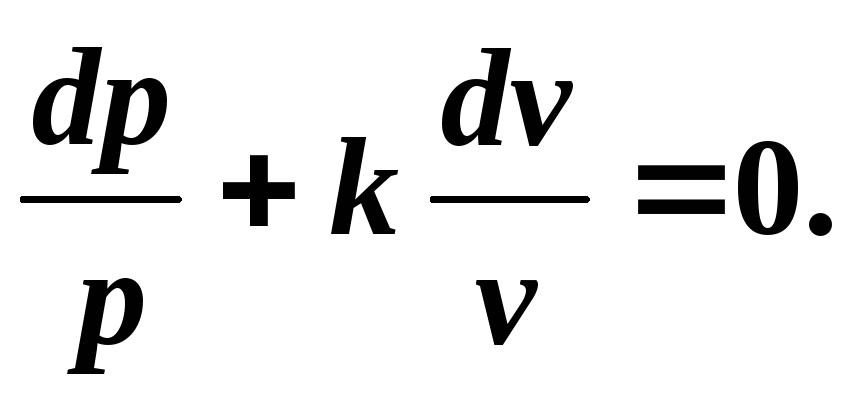 (5.6)
(5.6)
Интегрируя (5.6) при k = const , получим , откуда
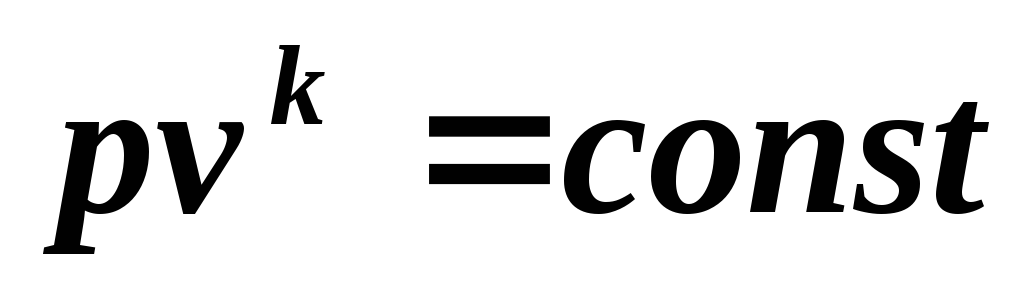 (5.7)
(5.7)
Уравнение (5.7) является уравнением адиабаты.
На
рис. 5.10 приведен адиабатный процесс
расширения газа в
 -диаграмме.
-диаграмме.
Из уравнения (5.7) следует:
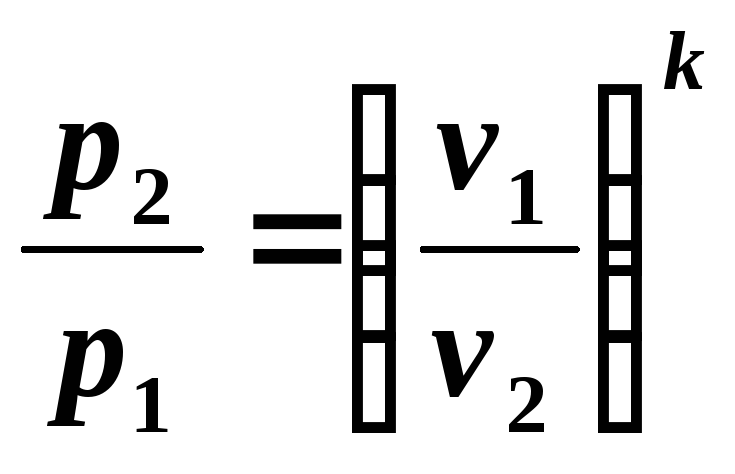 , (5.8)
, (5.8)
то есть при адиабатном расширении давление падает, а при сжатии возрастает.
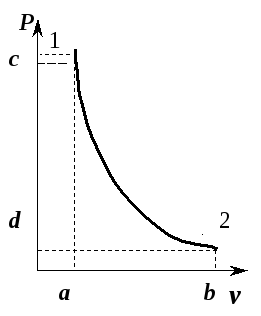
Рис. 5.10. Адиабата идеального газа
Учитывая, что в адиабатном процессе изменяются все три параметра состояния, необходимо выявить зависимости между v и T , p и T .
Зависимость между температурой T и объемом v можно получить из уравнения (5.8) и уравнений состояния, записанных для точек процесса 1 и 2 : Р 1 v 1 = RT 1 и Р 2 v 2 = RT 2 , откуда
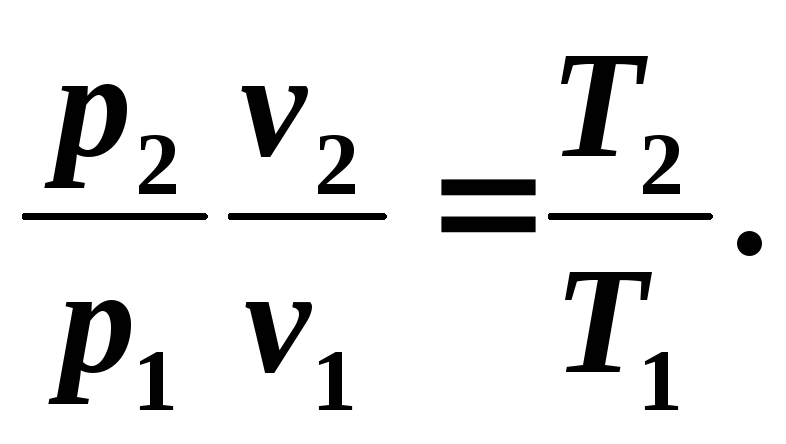 (5.9)
(5.9)
Из
уравнений (5.8) и (5.9) следует:
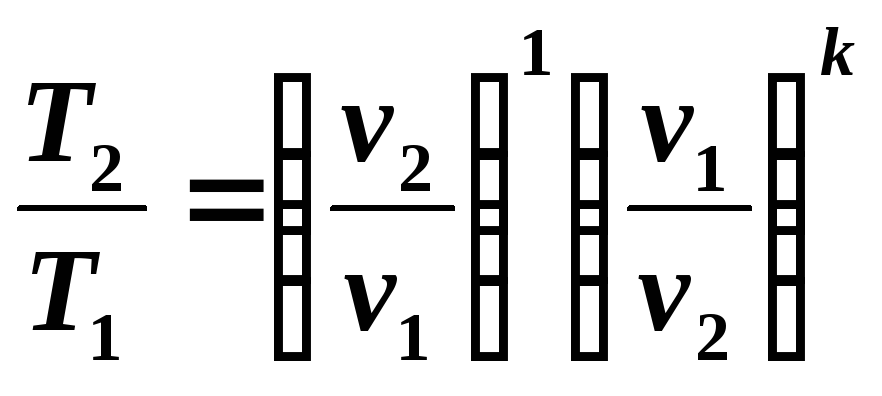
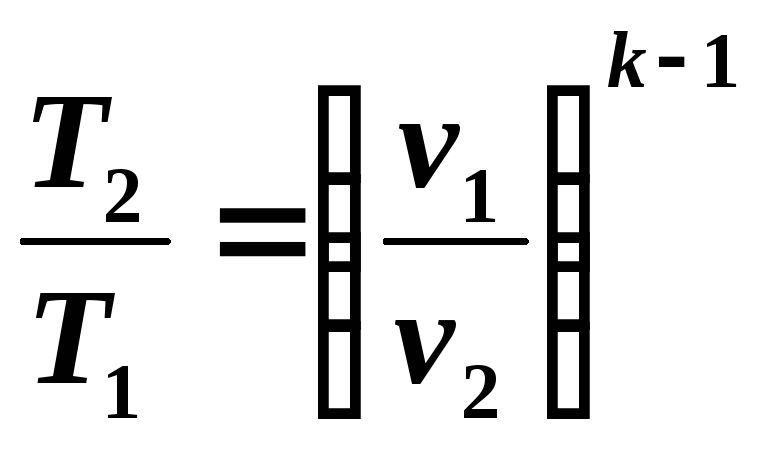 (5.10)
(5.10)
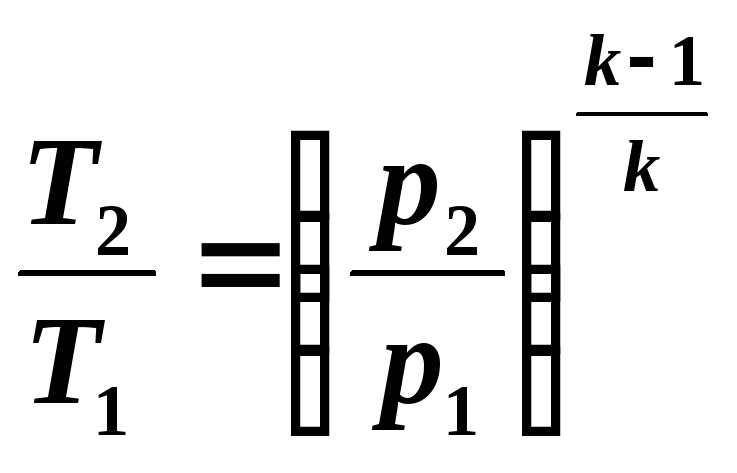 (5.11)
(5.11)
При
k
=
const
для вычисления работы адиабатного
процесса можно записать несколько
формул. Из уравнения
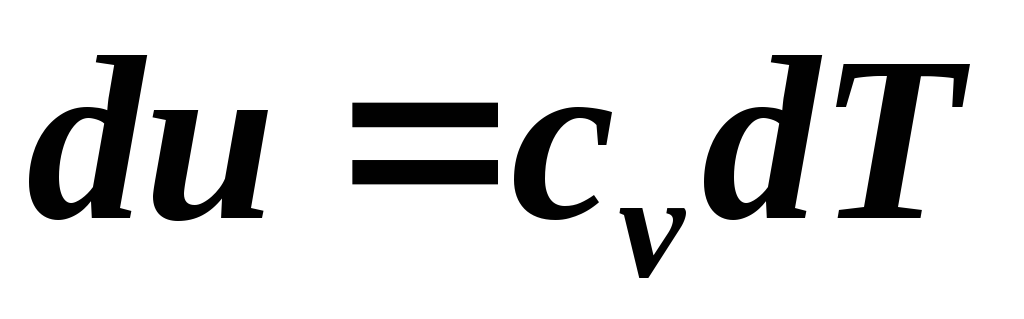 приc
v
=
const
имеем:
приc
v
=
const
имеем:
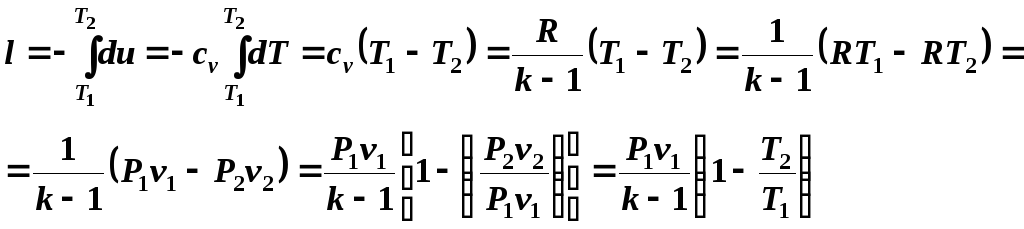 (5.12)
(5.12)
Учитывая соотношения (5.10) и (5.11), уравнение (5.12) запишем в виде:
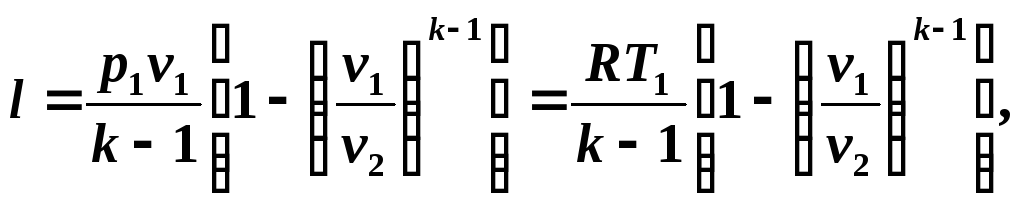
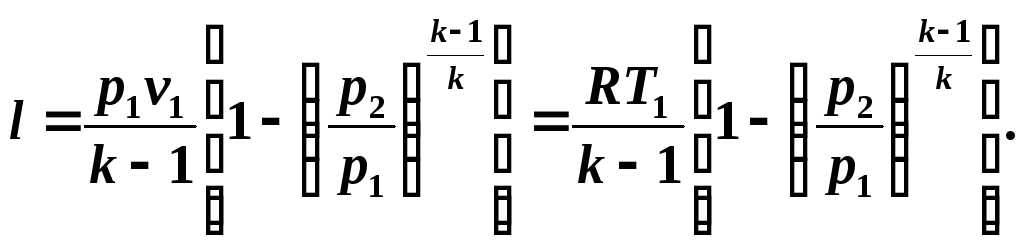
Располагаемая работа в адиабатном процессе определим из соотношения
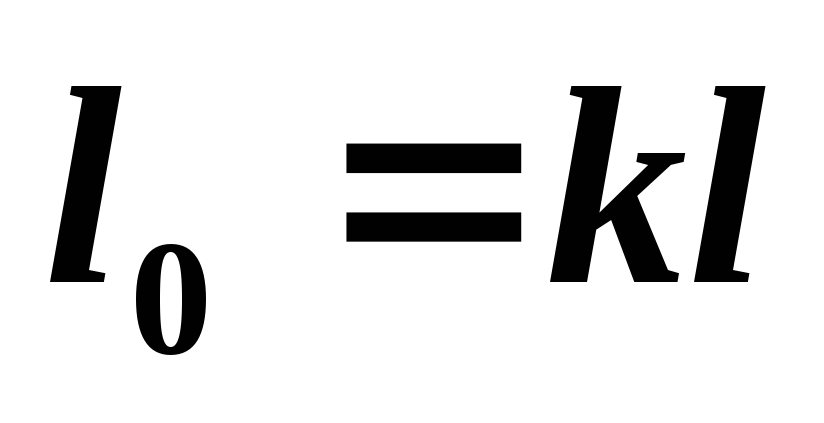 (5.14)
(5.14)
Для
обратимого адиабатного процесса
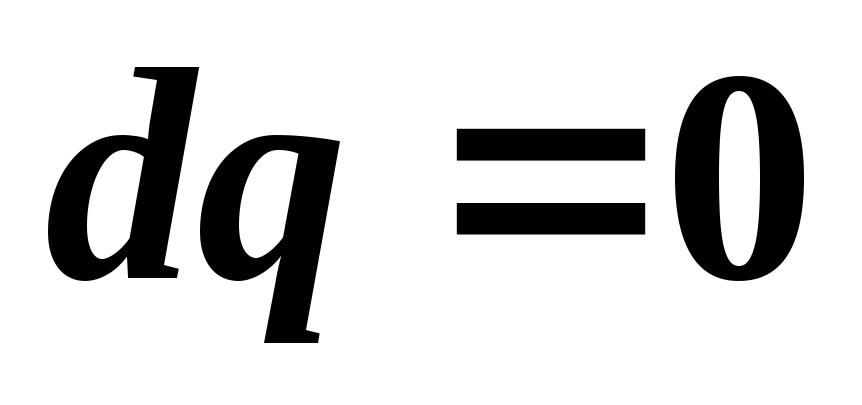 ,
поэтому
,
поэтому
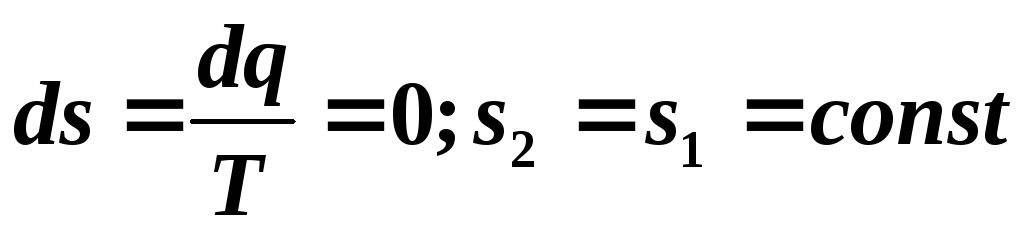 ,
то есть обратимый адиабатный процесс
будет изоэнтропным и в
,
то есть обратимый адиабатный процесс
будет изоэнтропным и в
 -диаграмме
изображается прямой линией, параллельной
оси
-диаграмме
изображается прямой линией, параллельной
оси (рис. 5.11). Процесс адиабатного расширения
изображается вертикальной прямой 2-1,
идущей вниз, а процесс адиабатного
сжатия 1-2 – вертикальной прямой, идущей
вверх.
(рис. 5.11). Процесс адиабатного расширения
изображается вертикальной прямой 2-1,
идущей вниз, а процесс адиабатного
сжатия 1-2 – вертикальной прямой, идущей
вверх.
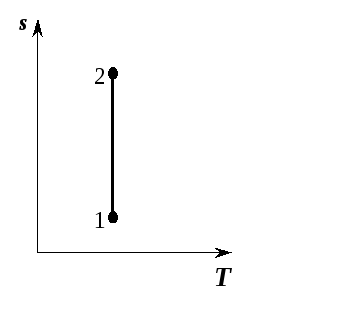
Рис.
5.11. Адиабатный процесс в
 -диаграмме
-диаграмме
Теплоемкость
в адиабатном процессе равна нулю:
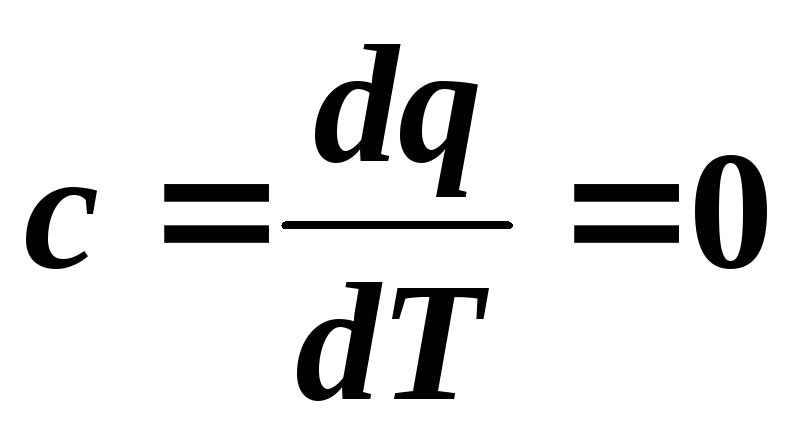 .
.
|
|
|
Рис. 5.12. Схема распределения энергии в адиабатном процессе:
а- при расширении газа; б – при сжатии газа
Политропный процесс
Политропный процесс – любой произвольный процесс изменения состояния рабочего тела, протекающий при постоянной теплоемкости с x , то есть c = c x = const. Линия процесса называется политропой.
Из определения политропного процесса следует, что основные термодинамические процессы (изохорный, изобарный, изотермический, адиабатный, если они протекают при постоянной удельной теплоемкости, являются частными случаями политропного процесса.
Другими словами, политропный процесс характеризуется одной и той же долей количества подводимой теплоты, расходуемой на изменение внутренней энергии системы.
Уравнение политропного процесса можно получить из уравнений первого закона термодинамики для идеального газа:
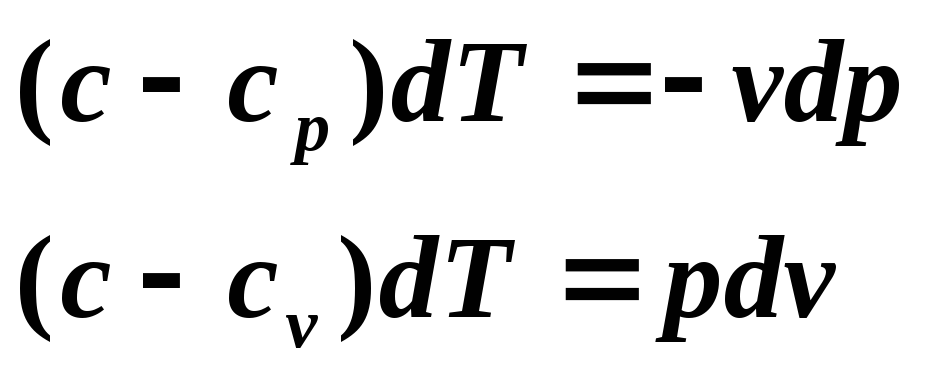
Разделим первое уравнение на второе
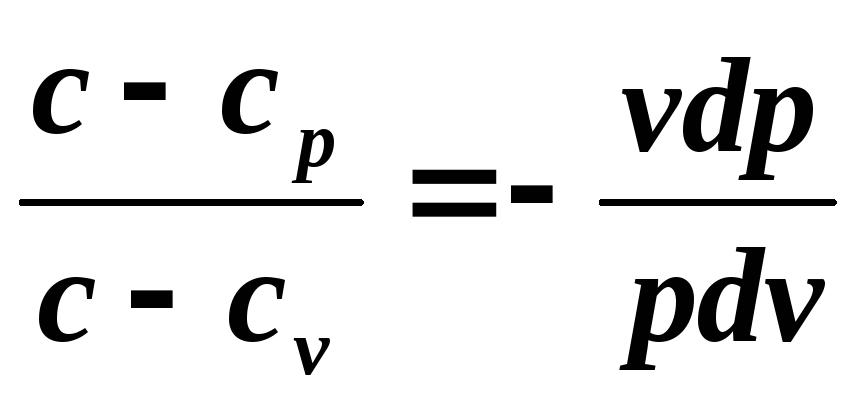
и обозначим
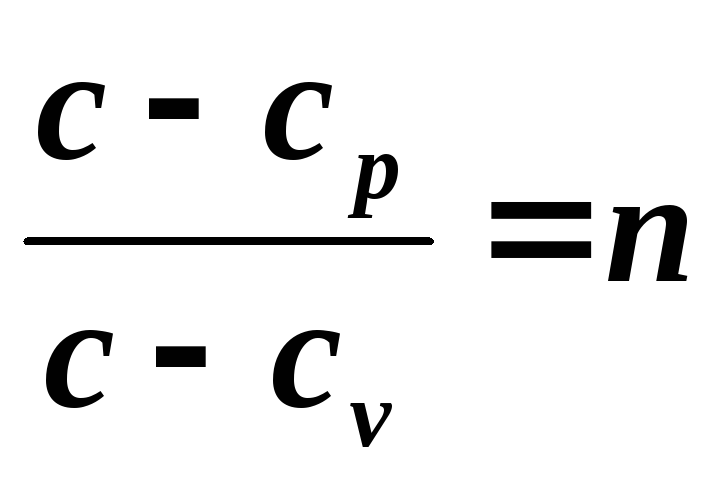 ,
,
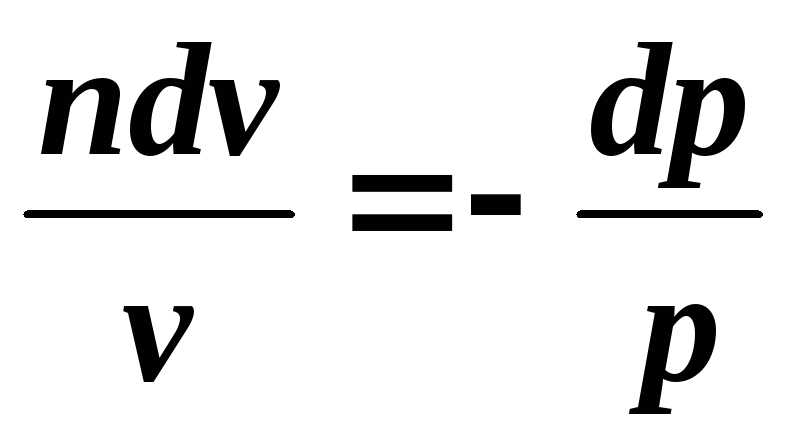
Интегрируя полученное соотношение в пределах от начала до конца процесса, находим:
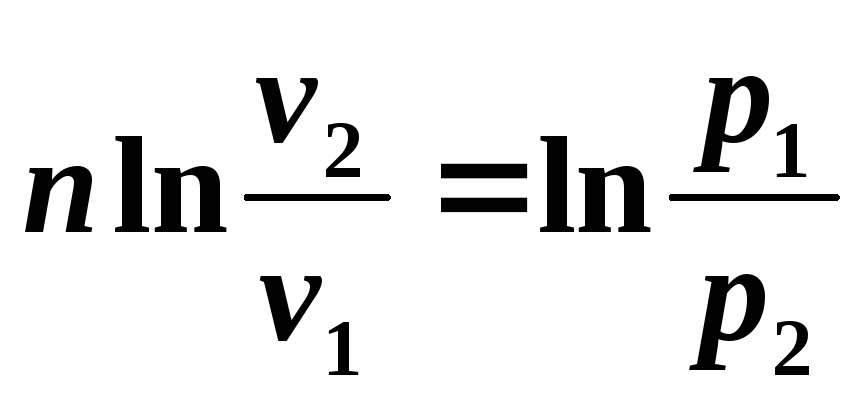 ,
,
или после потенцирования
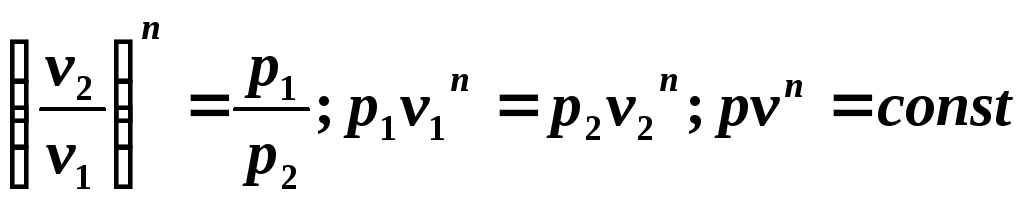
получаем
уравнение политропного процесса
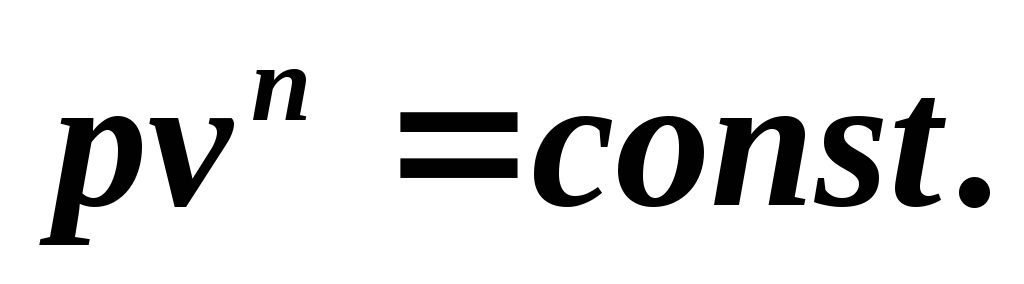
Поскольку уравнение политропы отличается от уравнения адиабаты только значением показателя n , то все соотношения между основными параметрами могут быть представлены формулами, аналогичными формулам для адиабатного процесса:
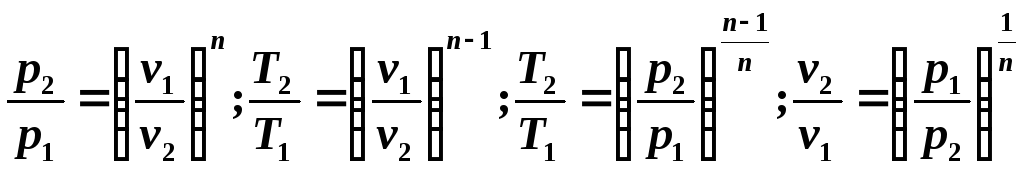
Удельная теплоемкость политропного процесса может быть определена из выражения для показателя политропы
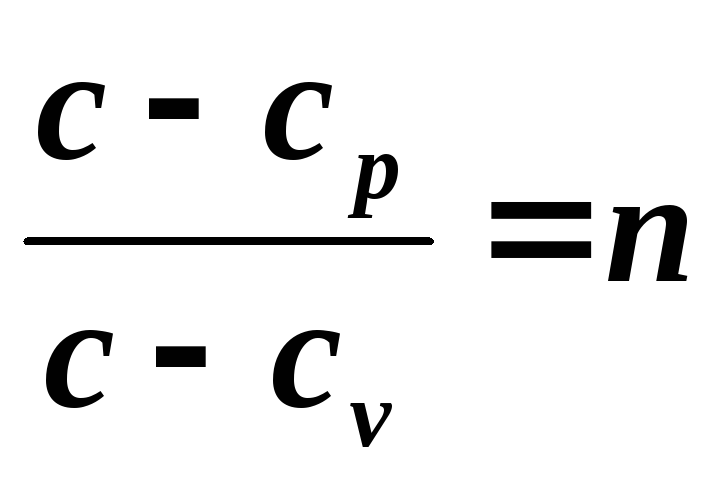 ,
откуда
,
откуда
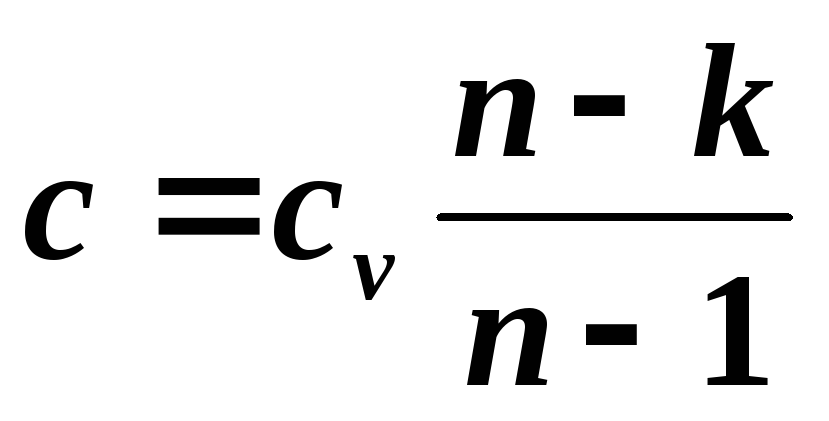 ,
,
где k – показатель адиабаты.
Последнее уравнение позволяет определить удельную теплоемкость политропного процесса для любого значения n . Если в это уравнение подставить значения для частных случаев, то можно получить:
|
Изохорный процесс: |
n = ; |
c = c v ; |
v = const. |
|
|
Изобарный процесс: |
n = 0 ; |
c = kc v = c p ; |
p = const . |
|
|
Изотермический процесс: |
n = 1 ; |
c = ; |
T = const. |
|
|
Адиабатный процесс: |
n = k ; | |||
3.8. Применение первого начала термодинамики
Термодинамический процесс, в котором система при переходе из состояния 1 в состояние 2 не обменивается теплотой с окружающей средой, называют адиабатическим .
На практике адиабатический процесс можно осуществить при быстром расширении (сжатии) газа, когда d Q º 0. Например, быстро протекающее расширение газов в цилиндре двигателя внутреннего сгорания. В двигателе Дизеля воздух быстро сжимается адиабатически в 15 и более раз, чем в двигателе внутреннего сгорания. При этом температура воздуха повышается до 3000 о С, поэтому при впрыскивании горючей смеси происходит ее самовоспламенение.
При возникновении ударной волны газ адиабатически сжимается и сильно нагревается, т.к. он не успевает отдать выделившуюся теплоту.
Метеориты при вхождении в атмосферу оплавляются и испаряются в основном по этой причине, а не из-за наличия трения и сопротивления при движении в атмосферном воздухе.
Адиабатическое расширение приводит к охлаждению системы, что используется при сжижении газов (адиабатическое размагничивание парамагнитных солей позволяет получить температуры, близкие к абсолютному нулю). К адиабатическим процессам относится и свободное расширение газов (рис. 3.6), т.к. Q=0, А=0, D U=0, D T=0.
Рис. 3.6
Первое начало термодинамики для адиабатического процесса представим в виде
Следовательно, при адиабатическом процессе газ совершает работу за счет убыли его внутренней энергии.
Теплоемкость вещества при адиабатическом процессе С =0 (d Q=0, dT ¹ 0).
Найдем вид уравнения состояния идеального газа для адиабатического процесса.
Перепишем уравнение (3.21) в виде:
Применив уравнение Майера (3.16), преобразуем (3.24) к виду
|
С р РdV + C v VdP = 0. |
(3.25) |
Уравнение (3.25), представим в виде
|
|
(3.26) |
где
|
(3.27) |
называют коэффициентом Пуассона
(показателем адиабаты) .После интегрирования (3.26) с учетом (3.27), получим
или
|
(3.28) |
Выражение (3.28) называют уравнением адиабаты (уравнение Пуассона ).
Используя уравнение Менделеева-Клапейрона (1.9) перепишем (3.28) в виде:
![]() .
.
Р- V диаграмма адиабатического процесса приведена на рис. 3.7.
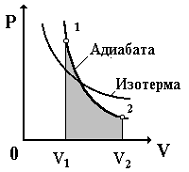
Рис. 3.7
Из рис. 3.7 видно, что кривая адиабаты идет круче, чем изотерма. Объясняется это тем, что при адиабатическом расширении идеального газа происходит не только уменьшение давления, но и понижение температуры, т.к. внутренняя энергия газа убывает. При адиабатическом сжатии газа растут давление и температура, не только из-за уменьшения объема, но и из-за увеличения внутренней энергии. Это можно наблюдать в компьютерной модели "Адиабатический процесс".
Компьютерная модель "Адиабатический процесс"
Модель предназначена для изучения адиабатического процесса, т. е. процесса квазистатического расширения или сжатия идеального газа, находящегося в сосуде с теплонепроницаемыми стенками. Можно изменять начальную температуру T газа. Приводится график зависимости p (V ) для адиабатического процесса, выводится энергетическая диаграмма, на которой представлены производимая газом работа A и изменение ΔU его внутренней энергии.
Согласно первому закону тер-модинамики Δ U = Q + A.
Изотермический, изохорный и изобарный изопроцессы широко применяются в технике. Так, закон Гей-Люссака положен в основу строения газовых термометров; закон Шарля «ра-ботает» в устройствах, которые называются автоклавами, и т. п. Термодинамика изучает еще один процесс, широко применяющий-ся на практике, в частности в тепловых двигателях. Это так называемый адиабатный процесс .
Адиабатный процесс — это термодинами-ческий процесс, который происходит в теп-лоизолированной системе, то есть при от-сутствии теплообмена с окружающими тела-ми.
Поскольку в таком случае Q = 0 , то в со-ответствии с первым законом термодина-мики вся выполненная работа идет на изме-нение внутренней энергии системы: A = Δ U.
Конечно, в реальных условиях достичь такого результата практически невозможно, поскольку не существует идеальных изоля-торов тепла. Но приблизиться к этому ус-ловию можно несколькими способами. На-пример, создать оболочки с низкой тепло-проводностью (по принципу термоса) или осуществить процесс настолько быстро, что-бы теплообмен между системой и окружа-ющими телами был непродолжительным и им можно было пренебречь.
При адиабатном сжимании га-за вся выполненная работа идет на увеличение внутрен-ней энергии тела: A = Δ U. При адиабатном расширении газа A’ = — Δ U, то есть газ вы-полняет работу за счет умень-шения собственной внутрен-ней энергии.
Например, быстрое сжатие газа вызывает возрастание внутренней энергии, которая равняется количеству выполненной работы A, и газ нагревается. На этом явлении, в частности, построено самовозгорание топ-ливной смеси в дизельных двигателях. И наоборот, если газ сам выполняет работу вследствие стремительного расширения, то его внутренняя энергия уменьшается, и тем-пература газа снижается. Это свойство адиабатного процесса положено в основу сжижения газа. Примером адиабатного процесса является также взрыв, плавление предохранителя при коротком замыкании и т. п.
Адиабаты, как и изотермы, не перекрещиваются между собой. Материал с сайта
Графически на координатной плоскости pV адиабатный процесс изображается кри-вой, которая называется адиабатой (рис. 2.5). Она падает круче, чем изотерма, поскольку при адиабатном процессе изменение дав-ления происходит за счет одновременного увеличения объема и уменьшения темпе-ратуры. Этот вывод подтверждает также фор-мула (24): p = nkТ, ведь увеличение объема газа ведет к уменьшению концентрации мо-лекул газа, и потому уменьшение давления обусловливают два параметра — температура газа T и концентрация молекул n.
Вследствие адиабатного расширения газа происходит изменение его состояния, которое характеризуется умень-шением внутренней энергии; при адиабатном сжимании газа его внутренняя энергия воз-растает.
На этой странице материал по темам:
Изопроцессы формулы шпаргалка
Физхимия адиабатный процесс
Физика адиабатный процесс
Адиабатический процесс шпаргалки по физике
Адиабатный процесс доклад
Вопросы по этому материалу:
В ходе изучения темы «Основы молекулярно-кинетической теории» нами были рассмотрены так называемые изопроцессы, то есть процессы, протекающие при неизменном одном из макроскопических параметров(давлении, объёме или температуре). При подстановке этих данных в уравнение Клапейрона эти условия несколько видоизменяли его. Теперь же мы проделаем схожий анализ, но уже с первым законом термодинамики:
Рассмотрим случай протекания процесса при неизменной температуре:
Следовательно:
![]()
А, значит, первый закон термодинамики приобретает вид:
Рассмотрев случай для выполнения над газом внешними силами положительной работы:
То есть, при изотермическом сжатии или расширении газ выделяет теплоту в окружающую среду.
Рассмотрим случай, когда процесс протекает при постоянном давлении:
Так как ни в одну термодинамическую величину не входит множитель , то никакое слагаемое первого закона термодинамики не обнуляется, и он сохраняет свой прежний вид:
Теперь рассмотрим, какие изменения произойдут в записи первого закона термодинамики, если процесс происходит в фиксированном объёме.
Следовательно:
![]()
А значит, первый закон термодинамики приобретает вид:
То есть теряется смысл использования изохорных процессов в тепловых двигателях, ведь вся энергия сгораемого топлива пойдёт на изменение внутренней энергии, и газ не будет совершать полезной работы.
Существует также ещё один очень важный процесс - адиабатный.
Определение. Адиабатный процесс - процесс, протекающий в теплоизолированной системе. То есть без подвода газу или выделения газом теплоты.
Первый закон термодинамики приобретает вид:
То есть в результате выполнения над газом работы внешними силами его внутренняя энергия, а следовательно, и температура увеличивается, а при выполнении работы газом - уменьшается.
Наглядными примерами последних двух утверждений являются следующие опыты.
1. В закрытом подвижным поршнем цилиндре находится небольшое количество топлива. После быстрого нажатия на поршень топливо воспламеняется.
2. В закрытом пробкой с продетым шлангом насоса сосуде находится небольшое количество воды. После нагнетания в сосуд определенно количества воздуха, пробка быстро вылетает и в сосуде наблюдается туман (рис. 1).


Рис. 1. Наглядные примеры адиабатных процессов ()
В двух случаях газ выполняет разные по знаку работы, и, следовательно, изменение внутренней энергии и температуры имеет разные знаки. В обоих случаях делается акцент на быстром изменении объёма потому, что невозможно создать идеально изолированную систему, но если рассматривать очень скоротечный процесс, то тепло не успеет передаться, и процесс можно считать адиабатным.
График адиабатных процессов в координатах P-V выглядит следующим образом (рис. 2).
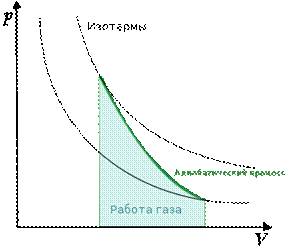
Рис. 2. График адиабатного процесса ()
Начиная со следующего урока, мы переходим к изучению нового раздела физики - электростатики.
Список литературы
- Мякишев Г.Я., Синяков А.З. Молекулярная физика. Термодинамика. - М.: Дрофа, 2010.
- Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. - М.: Илекса, 2005.
- Касьянов В.А. Физика 10 класс. - М.: Дрофа, 2010.
- Flash-fizika.narod.ru ().
- Youtube.com ().
- Nashaucheba.ru ().
Домашнее задание
- Стр. 82: № 635-639. Физика. Задачник. 10-11 классы. Рымкевич А.П. - М.: Дрофа, 2013. ()
- При адиабатном расширении 64 г кислорода, находящегося при нормальных условиях, температура увеличилась в 2 раза. Какую работу совершил газ?
- Определить количество теплоты, которое сообщено 2 кг гелия при постоянном объеме, если его температура повысилась на 100 К. На сколько изменилась внутренняя энергия газа и какая работа была совершена им?
- * Почему, если сбить вентиль баллона со сжатым воздухом, на горлышке баллона появится иней?