Основы молекулярно кинетической теории идеальный газ. Молекулярно-кинетическая теория
Экзаменационный проект за курс полной средней школы по предмету "Физика"
ГОУ СОШ № 7
г. Реутов Московской области 2008 год
Основные положения теории
Изображение атомов на поверхности кремния, полученное с помощью туннельного микроскопа.
Начиная с XVIII века, постепенно стала складываться система научных представлений о строении вещества, позднее названная молекулярно-кинетической теорией (МКТ). Молекулярно-кинетическая теория базируется на трёх положениях, обобщающих результаты большого количества экспериментальных данных:
Все тела состоят из мельчайших частиц – атомов, молекул и ионов. Таким образом любое вещество обладает дискретной структурой.
Частицы, образующие вещество, находятся в непрерывном хаотическом движении, которое называется тепловым.
Атомы, молекулы и ионы взаимодействуют друг с другом.
Рассмотрим эти положения несколько подробней.
Молекулярное строение вещества.
Моль вещества.
Число Авогадро. Количество вещества.
Современная физика не устанавливает пределы структурной делимости материи, однако, однозначно утверждает, что элементами, определяющими основные физические свойства тел, являются атомы, молекулы и ионы.
Атомом называется наименьшая частица данного химического элемента, являющаяся носителем его свойств.
Каждому химическому элементу соответствует свой атом.
Молекула – это устойчивая наименьшая частица данного вещества, обладающая его основными химическими свойствами.
Молекула состоит из атомов одинаковых или различных химических элементов.
Ион – электрически заряженная частица, которая образуется при потере или приобретении атомами и молекулами одного или нескольких электронов.
Атомное строение имеют инертные газы (гелий, аргон и др.), жидкости (ртуть) и твердые тела (медь, алмаз). Ряд кристаллических веществ, например, хлористый натрий, состоит из разноимённо заряженных ионов. Однако подавляющее большинство веществ образовано из молекул (углекислый газ, вода), поэтому понятие “молекула” часто используется как общий собирательный термин.
Современная экспериментальная техника позволяет наблюдать молекулярную структуру вещества, а также определять размеры атомов и молекул. Эти размеры весьма малы: для атомов они составляют величину порядка 10–10 м, для молекул их диапазон значительно шире - от 10–10 м для простейших молекул до 10–5 м для молекул сложных органических веществ.
Естественно, что при таких размерах масса атомов и молекул также очень мала, к примеру, масса молекулы водорода составляет 3.3·10–27 кг. Понятно, что оперировать такими величинами в практических расчетах не совсем удобно.
Поэтому было введено понятие относительной молекулярной (атомной) массы Mr, которое определяется как отношение массы молекулы (атома) данного вещества m0 к 1/12 массы атома углерода:
. (1)Число молекул в случае однокомпонентной системы, содержащей молекулы или атомы одного вида, можно найти по формуле:
где m – масса системы, выраженная в килограммах.
Из этой формулы видно, что N имеет очень большие значения, поэтому потребовалось введение некоторого относительного параметра, связанного с числом молекул N в системе, называемого количеством вещества.
В Международной системе единиц (СИ) в качестве такого параметра принят моль – количество вещества, в котором содержится столько же молекул или атомов, сколько атомов содержится в 0.012 кг углерода.
Таким образом, в одном моле любого вещества содержится одно и тоже число молекул или атомов, которое называется числом (постоянной) Авогадро и равно:
.Количество вещества определяется как число молей, равное отношению числа молекул N к числу Авогадро:
. (2)Масса одного моля вещества называется молярной массой. Она равна произведению массы одной молекулы вещества m0 на число Авогадро:
и измеряется в килограммах на моль: [M] = кг·моль–1.
Из (1), (3) и определения числа Авогадро следует, что между относительной молекулярной массой вещества Mr и его молярной массой M существует соотношение:
M = Mr·10–3 кг·моль–1.
Учитывая равенство
где m – масса вещества,
по формулам (2) и (3) легко получить ещё одно выражение для количества вещества:
, (4)т. е. количество вещества равно отношению массы этого вещества к его молярной массе.
Тепловое движение молекул.
Беспорядочность, хаотичность движения частиц - важнейшая черта теплового движения. Экспериментальным доказательством непрерывного характера движения молекул является диффузия и броуновское движение.
Диффузия - это явление самопроизвольного проникновения молекул одного вещества в другое.
В результате взаимной диффузии веществ происходит постепенное выравнивание их концентрации во всех областях занимаемого ими объёма.
Установлено, что скорость протекания процесса диффузии зависит от рода диффундирующих веществ и температуры. Одним из наиболее интересных явлений, подтверждающих хаотичность движения молекул, является броуновское движение. Оно представляет собой тепловое движение микроскопических (но состоящих из очень большого числа молекул) частиц вещества, находящихся во взвешенном состоянии в жидкости или в газе, впервые наблюдаемое Р. Броуном. Беспорядочность перемещения таких частиц объясняется тем, что сумма импульсов, полученных ими от молекул с разных сторон, может стать не равной нулю как вследствие разного числа ударов с разных сторон частицы, так и в результате того, что частицу с одной стороны могли ударить молекулы, обладающие большими скоростями, чем молекулы, ударившие ее с другой стороны.
Броуновское движение проявляется тем заметнее, чем меньше частицы и вязкость среды, и чем выше температура системы. Зависимость от температуры свидетельствует о том, что скорость хаотического движения молекул возрастает с увеличением температуры, именно поэтому его и называют тепловым движением.
Взаимодействие молекул.
Межмолекулярные силы имеют электромагнитную природу и сводятся к двум типам - притяжению и отталкиванию. Эти силы являются короткодействующими и проявляются лишь на расстояниях, сравнимых с размерами молекул. Силы притяжения и отталкивания быстро убывают с увеличением расстояния между молекулами, однако скорость их убывания различна. Сила отталкивания преобладает на малых расстояниях и неограниченно растёт по мере приближения расстояния между центрами масс молекул r к некоторой величине d, которую можно рассматривать как эффективный диаметр молекул.
Сила притяжения уменьшается с увеличением r намного медленнее силы отталкивания, поэтому существует некоторое значение межмолекулярного расстояния r = r0, на котором силы отталкивания и притяжения компенсируют друг друга, так что результирующая сила межмолекулярного взаимодействия обращается в нуль.
Изменение агрегатного состояния вещества
Агрегатные состояния
Всякое вещество может находиться в трёх агрегатных состояниях: в твёрдом, жидком и газообразном.
В газах средняя кинетическая энергия теплового движения молекул значительно превосходит потенциальную энергию их взаимодействия. В этом случае силы взаимодействия между молекулами весьма слабо влияют на характер их относительного движения, поскольку молекулы находятся на достаточно большом расстоянии друг от друга. По мере уменьшения температуры или при сжатии взаимодействие молекул начинает играть настолько существенную роль, что газ в конце концов переходит в конденсированное состояние - жидкость.
В жидкости средняя энергия взаимодействия молекул примерно равна средней энергии теплового движения. Тепловое движение нарушает связь между молекулами и приводит к перемещению их относительно друг друга внутри объёма жидкости. В связи с этим жидкость принимает форму сосуда, в который она помещена.
Под твердыми телами обычно подразумеваются кристаллы, характерной особенностью которых является регулярное расположение в них атомов или ионов. О совокупности точек, в которых расположены атомные ядра, говорят как о кристаллической решетке, а сами эти точки называют узлами решетки.
Тепловое движение атомов или ионов кристалла носит в основном колебательный характер. Однако, поскольку в кристалле кинетическая энергия колебательного движения атомов значительно меньше абсолютного значения потенциальной энергии их взаимодействия, то тепловое движение не может разрушить связь между атомами. Поэтому твердое тело, в отличие от жидкости, сохраняет свою форму и обладает большой механической прочностью.
Кроме кристаллических тел существуют аморфные тела. Они, хотя и рассматриваются обычно как твердые, представляют собой переохлажденные жидкости. Если рассматривать некоторый атом аморфного тела как центральный, то ближайшие к нему атомы будут располагаться в определенном порядке, но по мере удаления от "центрального" атома этот порядок нарушается и расположение атомов становится случайным. К аморфным телам относятся стекло, пластмассы и т.д.
Переход из одного агрегатного состояния в другое (при постоянном давлении) происходит при строго определённой температуре и всегда связан с выделением или поглощением некоторого количества тепла. Переход вещества из одного состояния в другое происходит не мгновенно, а в течении некоторого времени, когда два состояния вещества существуют одновременно в тепловом равновесии.
Плавление и кристаллизация
По мере возрастания температуры энергия колебательного движения атомов в твёрдом теле возрастает и, наконец, наступает такой момент, когда связи между атомами начинают разрываться. При этом твердое тело переходит в жидкое состояние. Такой переход называется плавлением. При фиксированном давлении плавление происходит при строго определённой температуре.
Количество тепла, необходимое для превращения единицы массы вещества в жидкость при температуре плавления, называют удельной теплотой плавления .
Для плавления вещества массой m необходимо затратить количество теплоты равное:
При охлаждении расплавленного твёрдого тела происходит обратный процесс, называемый кристаллизацией. Образование кристалла также происходит при постоянной температуре, равной температуре плавления. При кристаллизации жидкости выделяется такое же количество теплоты, какое поглощается при плавлении вещества той же массы.
Аморфные тела в противоположность кристаллам не имеют определенной температуры плавления.
Испарение и конденсация.
Как в жидкостях, так и в твердых телах всегда имеется некоторое число молекул, энергия которых достаточна для преодоления притяжения к другим молекулам и которые способны оторваться от поверхности жидкости или твердого тела и перейти в окружающее их пространство. Этот процесс для жидкости называется испарением (или парообразованием), а для твердых тел - сублимацией (или возгонкой).
Количество тепла Q, которое необходимо сообщить жидкости для испарения единицы её массы при постоянной температуре, называется удельной теплотой парообразования r.
Количество теплоты, которое надо затратить, чтобы перевести в пар жидкость массой m,
В результате хаотического движения над поверхностью жидкости молекула пара, попадая в сферу действия молекулярных сил, вновь возвращается в жидкость. Этот процесс называется конденсацией. Испарение жидкости происходит при любой температуре и тем быстрее, чем выше температура, больше площадь свободной поверхности испаряющейся жидкости и быстрее удаляются образовавшиеся над жидкостью пары.
Следует обратить внимание, что процесс парообразования связан с увеличением внутренней энергии вещества, а процесс конденсации - с уменьшением ее.
Насыщенные и ненасыщенные пары. Влажность.
Если за одно и то же время число испаряющихся и конденсирующихся молекул пара одинаково, то число молекул пара над жидкостью будет оставаться постоянным. Такое состояние называют динамическим равновесием пара и жидкости. Пар, находящийся в динамическом равновесии с жидкостью, называют насыщающим (или насыщенным). При неизменной температуре плотность насыщающего пара над жидкостью остается постоянной.
Пар, плотность которого меньше плотности насыщающего пара при той же температуре, называют ненасыщающим (или ненасыщенным).
Ненасыщенный пар подчиняется законам идеального газа.
Частным случаем испарения является кипение. Это процесс интенсивного парообразования не только со свободной поверхности, но и в объеме жидкости. В объеме образуются пузыри, заполненные насыщенным паром. Они поднимаются вверх под действием выталкивающей силы и разрываются на поверхности. Центрами их образования являются мельчайшие пузырьки посторонних газов или частиц различных примесей.
Процесс превращения жидкости в пар требует затрат энергии на разрыв связей между молекулами жидкости и на работу против сил внешнего давления. Давление насыщенного пара Pнас внутри пузырька, находящегося у поверхности жидкости, равно сумме внешнего давления на жидкость Рвн и давления под искривленной поверхностью жидкости.
Рнас= Рвн+ 2/r , (7)
где r - радиус пузырька,
- коэффициент поверхностного натяжения.
Если пузырек имеет размеры порядка нескольких миллиметров и более, то вторым слагаемым можно пренебречь и, следовательно, для больших пузырьков при неизменном внешнем давлении жидкость закипает, когда давление насыщенного пара в пузырьках становится равным внешнему давлению.
Для того чтобы судить, много или мало водяных паров находится в воздухе, вводят понятие влажности. Абсолютная влажность - количество пара, выраженное в килограммах, содержащееся в 1 м3 при данной температуре, т.е. абсолютная влажность равна плотности паров воды. Относительная влажность В - это отношение абсолютной влажности к плотности насыщенного пара при данной температуре.
100% . (8)Плотность насыщенного водяного пара при данной температуре есть величина табличная. Для определения относительной влажности надо знать абсолютную влажность, которую можно определить по точке росы.
Точке росы соответствует температура, при которой пар, находящийся в воздухе, становится насыщающим.
Молекулярно-кинетическая теория идеальных газов
Тепловое равновесие.
Температура. Шкала температур Цельсия.
Молекулярная физика и термодинамика изучают свойства и поведение макроскопических систем, т.е. систем, состоящих из огромного числа атомов и молекул. Типичные системы, с которыми мы сталкиваемся в повседневной жизни, содержат около 1025 атомов.
При исследовании таких систем важнейшими являются макроскопические величины, непосредственно измеряемые опытным путём и характеризующие свойства всей совокупности молекул в целом. Учитывая необычайную сложность макросистем, следует начать изучение с наиболее простых объектов – систем, состояние которых не меняется со временем. Состояние макроскопической системы, в котором она может находится неопределённо долгое время, называется равновесным (о нём говорят также, как о состоянии теплового равновесия).
Равновесное состояние системы в целом может быть описано при помощи величин, называемых макроскопическими параметрами, к числу которых относят давление, объем и т. д. Каждый из параметров характеризует некоторое свойство системы. Так объем V мера свойства системы занимать ту или иную область пространства; давление Р – мера свойства системы сопротивляться внешнему изменению ее объёма.
В состоянии теплового равновесия макроскопические параметры не меняются со временем, остаются постоянным.
Одним из наиболее важных параметров, характеризующих равновесные свойства макроскопической системы, является температура. Введем этот параметр, для чего рассмотрим два тела, которые могут взаимодействовать и обмениваться энергией. Этот тип взаимодействия, который называется тепловым, приводит к тому, что в результате столкновений молекул в области контакта двух тел происходит передача энергии от быстрых молекул к медленным. Это означает, что энергия движения атомов в одном теле уменьшается, в другом – увеличивается. Тело, которое теряет энергию, называют более нагретым, а тело, к которому энергия переходит – менее нагретым. Такой переход энергии продолжается до тех пор, пока не установится состояние теплового равновесия. В состоянии теплового равновесия степени нагретости тел одинаковы. Для характеристики степени нагретости тела вводят параметр, называемый температурой.
Из опыта известно, что при изменении температуры изменяются размеры тел, электрическое сопротивление и другие свойства. Таким образом, температуру можно определить по изменению какого-либо удобного для измерения физического свойства данного вещества.
Чаще всего для измерения температур используют свойство жидкости изменять объем при нагревании и охлаждении. Прибор, с помощью которого измеряется температура, называется термометром.
Обыкновенный жидкостной термометр состоит из небольшого стеклянного резервуара, к которому присоединена стеклянная трубка с узким внутренним каналом. Резервуар и часть трубки наполнены ртутью или другой жидкостью. Температуру среды, в которую погружен термометр, определяют по положению верхнего уровня ртути в трубке. Деления на шкале условились наносить следующим образом. Цифру 0 ставят в том месте шкалы, где устанавливается уровень столбика жидкости, когда термометр опущен в тающий снег, цифру 100 – в том месте, где устанавливается уровень столбика жидкости, когда термометр погружен в пары воды, кипящей при нормальном давлении (105 Па). Расстояние между этими метками делят на 100 равных частей, называемых градусами. Такая температурная шкала создана Цельсием. Градус по шкале Цельсия обозначают °С.
Кроме макроскопических параметров вводят параметры системы, связанные с индивидуальными характеристиками составляющих её частиц, называемые микроскопическими. К их числу относятся в первую очередь масса частиц, их скорость, кинетическая энергия.
Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа.
Теория создана немецким физиком Р. Клаузисом в 1957 году для модели реального газа, которая называется идеальный газ. Основные признаки модели:
расстояния между молекулами велики по сравнению с их размерами;
взаимодействие между молекулами на расстоянии отсутствует;
при столкновениях молекул действуют большие силы отталкивания;
время столкновения много меньше времени свободного движения между столкновениями.
Молекулярно-кинетическая теория (МКТ) устанавливает связи между макро- и микропараметрами идеального газа. Основное уравнение МКТ выражает выражает связь давления газа со средней кинетической энергией поступательного движения молекул. Давление газа на стенки сосуда является результатом многочисленных ударов молекул. При каждом ударе стенка получает силовой импульс, величина которого зависит от скорости молекул и, следовательно, от энергии их движения. При огромном числе ударов создается постоянное давление газа на стенку. Число ударов зависит от концентрации молекул n. Таким образом, можно ожидать, что давление газа связано с концентрацией молекул и с энергией их движения. Получим основное уравнение МКТ.
Рассмотрим сферический объём радиуса R, в котором находится N молекул идеального газа. Рассмотрим движение одной из них. Допустим, что молекула двигалась прямолинейно с импульсом
ударилась о стенку под углом ψ к нормали и отскочила от неё под тем же углом, имея импульс . Найдём импульс, переданный молекулой стенке при ударе. Из закона сохранения импульса:Т. к. удар упругий,
и = 0, поэтому направлен по нормали к стенке и по модулю равен: .Путь, который молекула проходит от одного удара о стенку до другого, равен хорде АВ, т. е. величине 2Rcosψ.
Найдем число ударов молекулы о стенку за одну секунду. Оно равно отношению скорости молекулы
к пути, проходимому молекулой от одного столкновения со стенкой до другого: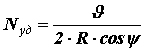 .
.
Сталкиваясь со стенками сосуда, одна молекула за одну секунду сообщает ей импульс
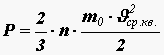
Суммарный импульс, сообщенный всеми N молекулами стенке сосуда за одну секунду будет равен
.Из II закона Ньютона следует, что импульс, сообщённый за единицу времени стенке, численно равен силе, поэтому сила давления, действующая на поверхность сосуда, равна
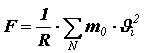 .
.
Давление найдём, разделив силу на площадь поверхности сферического сосуда:
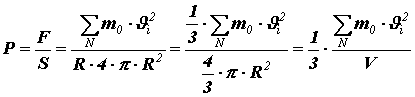 ,
– объём сосуда с газом.
,
– объём сосуда с газом.
Перепишем полученное равенство в виде:
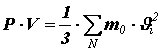
Помножив и поделив правую часть на число молекул N в объёме V, получим:
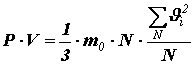 или
или Здесь введена величина
– средняя квадратичная скорость, равная корню квадратному из суммы квадратов всех скоростей, делённой на число молекул: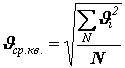 . (10)
. (10)
Это уравнение называется основным уравнением молекулярно-кинетической теории идеального газа.
Получим связь давления со средней кинетической энергией поступательного движения молекулы
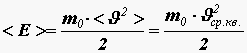 . (12)
. (12)
Из формулы (11)
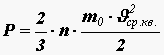 , следовательно:
, следовательно:
Таким образом, давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы. Это утверждение можно считать другой формулировкой основного уравнения молекулярно-кинетической теории идеального газа.
Закон Дальтона.
Рассмотрим газ, состоящий из молекул различных веществ, который находится в объёме V. Вследствие хаотического теплового движения молекулы каждой компоненты смеси будут распределены по объёму равномерно, т.е. так как если бы остальные компоненты газа отсутствовали. Из–за постоянных соударений молекул друг с другом, сопровождающихся частичным обменом между ними импульсами и энергиями, в смеси устанавливается тепловое равновесие. Всё это приводит к тому, что давление каждой из компонент смеси не будет зависеть от присутствия остальных.
Тогда результирующее давление определяется суммарным давлением всех компонентов, т.е. для смеси газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов.
, (14)где k – номер газовой компоненты в смеси, Pk – ее парциальное давление, т.е. то давление, которое имел бы k–ый газ, если бы только он один занимал весь объём, занимаемый смесью.
Средняя квадратичная скорость молекул.
Из основного уравнения молекулярно-кинетической теории можно получить формулу для расчета средней квадратичной скорости молекул
Произведение массы одной молекулы m0 на число молекул в единице объема n равно плотности вещества r:=r m0×n.
Таким образом,
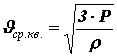 . (15)
. (15)
кспериментальные газовые законы
Изопроцессы. Законы Бойля-Мариотта, Гей-Люссака, Шарля.
Всякое изменение состояния газа называется термодинамическим процессом.
Простейшими процессами в идеальном газе являются изопроцессы. Это процессы, при которых масса газа и один из его параметров состояния (температура, давление или объем) остаются постоянными.
Изопроцесс, протекающий при постоянной температуре, называется изотермическим.
Экспериментально Р. Бойлем и Э. Мариоттом было установлено, что при постоянной температуре произведение давления газа на объем для данной массы газа есть величина постоянная (закон Бойля–Мариотта):
Графически этот закон в координатах РV изображается линией, называемой изотермой (рис.1).
Изопроцесс, протекающий в идеальном газе, в ходе которого давление остается постоянным, называется изобарным.
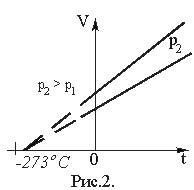
Зависимость объема газа от его температуры при постоянном давлении была установлена Л. Гей-Люссаком, который показал, что объем газа данной массы при постоянном давлении возрастает линейно с увеличением температуры (закон Гей-Люссака):
V = V0·(1 + ·t), (17)
где V – объем газа при температуре t, °С; V0 – его объем при 0°С.
Величина
называется температурным коэффициентом объемного расширения. Для всех газов = (1/273°С–1). Следовательно, ·t). (18)Графически зависимость объема от температуры изображается прямой линией – изобарой (рис. 2). При очень низких температурах (близких к – 273°С) закон Гей–Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.
Изопроцесс, протекающий в газе, при котором объем остается постоянным, называется изохорным.
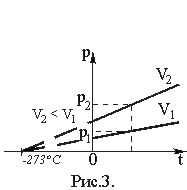
Исследования зависимости давления данной массы газа от температуры при неизменном объеме были впервые проведены французским физиком Шарлем. Им было установлено, что давление газа данной массы при постоянном объеме возрастает линейно с увеличением температуры (закон Шарля):
t). (19)Здесь P – давление газа при температуре t, °С; P0 – его давление при 0 °С.
Величина
называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов = 1/273 °С–1. Таким образом, ·t). (20)Графическая зависимость давления от температуры изображается прямой линией – изохорой (Рис. 3).
Абсолютная шкала температур.
Основы молекулярно-кинетической теории к
Основным положением молекулярно-кинетической теории является утверждение, что все тела состоят из мельчайших частиц (молекул, атомов и т.д.), которые движутся и взаимодействуют между собой. Доказательствами молекулярного строения вещества являются дробление тел, плавление, испарение, диффузия, броуновское движение и т.д.
Молярной массой M вещества называется масса такого количества молекул данного вещества, которое содержится в углероде 12 C массой 12 г. Молярную массу вещества можно узнать по таблице Менделеева, сложив атомные массы всех атомов, входящих в молекулу этого вещества. При этом молярная масса будет измеряться в г/моль. Для перевода в систему СИ это значение следует умножить на 10 -3 . При этом молярная масса измеряется в кг/моль. Так, например, молярная масса водорода H 2 равна 2 г/моль=2⋅10 3 кг/моль.
В одном моле любого вещества содержится N A = 6,022⋅10 23 моль -1 молекул. Число N A называется постоянной Авогадро. Масса одной молекулы m0 выражается формулой
Количеством вещества v называется отношение числа молекул N к числу Авогадро N A:
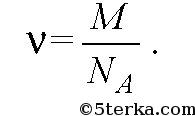
Если m - масса вещества, то
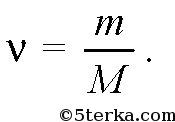
Идеальным газом называется газ, в котором молекулы движутся свободно и взаимодействуют между собой и со стенками сосуда только при столкновениях. Модель идеального газа удовлетворительно описывает достаточно разреженные газы.
Среднеквадратичной скоростью молекул
называется следующая физическая величин
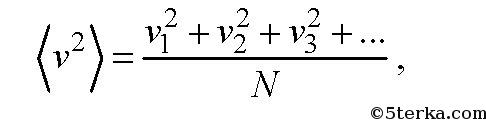
где v 1 , v 2 , v 3 ,... - скорости молекул: первой, второй, третьей, и так далее до N. Отметим, что средняя скорость молекул равна нулю и не равна
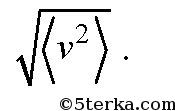
Концентрацией молекул n называется отношение числа молекул N в объеме V к этому объему V:
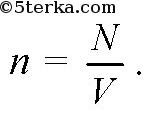
Давление p можно выразить следующей формулой
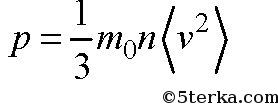
Это уравнение носит название основного уравнения молекулярно кинетической теории (МКТ) газов. Это уравнение можно переписать в виде
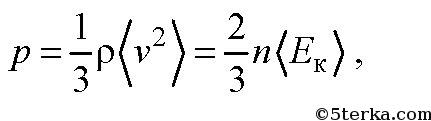
где ρ - плотность газа,
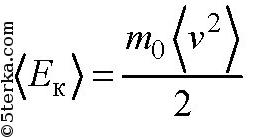
Средняя кинетическая энергия молекулы газа. Средняя кинетическая энергия
связана с температурой T газа формулой
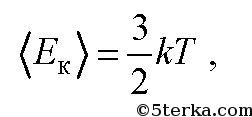
где k-постоянная Больцмана. Она численно равна
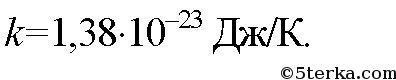
Можно доказать следующую формулу:
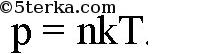
Из нее следует уравнение Менделеева-Клапейрона
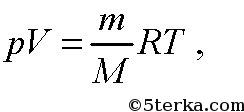
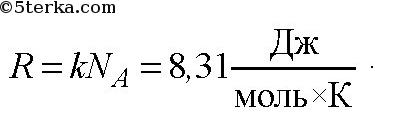
Универсальная газовая постоянная.
При неизменной массе и составе газа
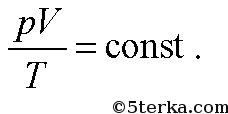
Если же постоянна еще и температура, то
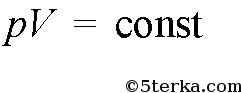
(изотермический процесс), если давление постоянно, то

(изобарический процесс), если объем постоянен, то
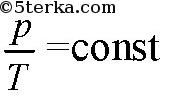
(изохорический процесс).
Водяной пар всегда присутствует в атмосфере Земли, как малая примесь, но он во многом определяет погоду. Влажность воздуха можно характеризовать парциальным давлением пара p или плотностью пара ρ (абсолютная влажность). Насыщенным паром называется пар, находящийся в динамическом равновесии со своей жидкостью. При определенной температуре существует такое давление, при котором водяной пар становится насыщенным. Такое давление р нас называется давлением насыщенного пара. Это давление можно найти по таблице в задачнике. Относительной влажностью φ называется отношение парциального давления пара p к давлению насыщенного пара
Согласно модели идеального газа молекулы все время находятся в беспо-рядочном движении, сталкиваются между собой и со стенками сосуда, в котором пре-бывают. В момент столкновения молекулы со стенкой она действует на нее с силой, им-пульс которой, согласно второму закону Нью-тона, равняется изменению ее импульса (количества движения): F̅ t = Δ(m ͞ v). Это значит, что изменение модуля импульса всех мо-лекул ΣΔ(mv i) при ударе равнозначно дей-ствию усредненного значения силы F̅ в течение времени t. Это суммарное действие молекул вызывает давление газа, которое по определению равно p = F / S .
Давление газа вызывают уда-ры о стенку сосуда большого количества молекул, передаю-щих ему импульс.
Рассмотрим идеальный газ, который на-ходится в сосуде объемом V. Для простоты расчетов выберем его в форме параллеле-пипеда (рис. 1.15). Пусть в нем находится N молекул массой m 0 каждая; их концентра-ция равна n = N / V . Поскольку молекулы дви-жутся беспорядочно (условие динамичес-кого хаоса для идеального газа), то до-статочно определить давление на одну из стенок, поскольку на другие стенки мо-лекулы будут создавать такое же давление. Для простоты изложения сначала будем счи-тать, что все они имеют одинаковые ско-рости V.
Представим отдельный слой газа, перпенди-кулярный координатной плоскости ZY. В си-лу хаотичности движения количество моле-кул, влетающих в этот слой справа, равня-ется количеству молекул, вылетающих из него слева. Очевидно, что и те и другие передают данному слою импульс: влета-ющие слева (рис. 1.16) несут импульс m 0 v x , где v x — проекция скорости на ось Х ; вы-летающие из него выносят импульс — m 0 v x , в целом передавая ему импульс 2 m 0 v x . Итак, со стороны всех молекул Z , влетающих в отдельный слой, стенка получает импульс 2 Zm 0 v x .
Количество молекул Z , которые сталки-ваются со стенкой площадью S за время t, можно определить по их концентрации в объеме отдельного слоя: Z = nv x tS, где n — концентрация молекул. Поскольку к стенке долетают лишь те молекулы, которые имеют положительную проекцию скорости на ось X (v x > 0), то их количество будет составлять половину от числа молекул, пересекающих плоскость отдельного слоя газа:
Z = nv x tS / 2.
Итак, со стороны всех молекул, нахо-дящихся в отдельном слое, стенка получает общий импульс:
F x t = 2 . nv x tSm 0 v x / 2.
Разделив левую и правую части равен-ства на St, получим:
F x / S = p = nm 0 v 2 x .
Предположения, что скорости всех мо-лекул одинаковы, было сделано с целью упрощения вывода уравнений. На самом же деле диапазон их значений довольно широк — от 0 до определенного максималь-ного значения v max . Поэтому в предыдущем уравнении для определения давления газа правильнее будет брать средний квадрат проекции скорости v x . Тогда оно будет иметь вид:
p = nm 0 v̅ 2 х.
Понятно, что аналогичные соображения будут справедливы для стенок, лежащих в других координатных плоскостях:
p = nm 0 v̅ 2 y ,
p = nm 0 v̅ 2 z .
Средний квадрат скорости имеет смысл среднестатистического значения скорости. Материал с сайта
Очевидно, что вследствие хаотического движения молекул v̅ 2 x = v̅ 2 y = v̅ 2 z . По мате-матическому определению средний квадрат скорости равен v̅ 2 = (v̅ 2 x + v̅ 2 y + v̅ 2 z). Отсюда v̅ 2 x = (1 / 3) . v̅ 2 . Подставив это выражение в урав-нение p = nm 0 v̅ 2 х , получим окончательное уравне-ние для определения давления идеального газа :
p = (1 / 3) . nm 0 v̅ 2 .
Эта формула является основным уравне-нием молекулярно-кинетической теории (МКТ) иде-ального газа, которое определяет связь меж-ду макропараметром термодинамической си-стемы — давлением идеального газа и харак-теристиками его микроскопического состо-яния. Таким образом, оно определяет дав-ление газа как статистическую величину по-средством микропараметров системы — кон-центрации, массы и скорости молекулы.
Поскольку nm 0 = ρ , где ρ — плотность газа, основ-ное уравнение молекулярно-кинетической теории идеального газа будет иметь еще и такой вид:
p = (1 / 3) . ρv̅ 2 .
Основное уравнение MKT яв-ляется мостиком между двумя подходами в толковании теп-ловых явлений и процессов — термодинамическим и молеку-лярно-кинетическим.
На этой странице материал по темам:
Идеальный газ лекция основное уравнение мкт
Как изменяется импульс слоя газа за счет молекул вылетающих в него
-
На данном уроке мы будем выводить основное уравнение молекулярно-кинетической теории (МКТ), которое связывает макропараметры газа с микропараметрами отдельных молекул.
Вспомним основные сведения про модель идеального газа:
Молекулы движутся хаотически;
Механизм давления идеального газа - это соударение отдельных молекул со стенками сосуда.
Пусть идеальный газ находится в цилиндрическом сосуде (см. Рис. 1). Определим давление p этого газа на поршень.
Рис. 1. Идеальный газ (молекулы) в цилиндрическом сосуде
По определению давление - величина, равная отношению силы (F ), действующей перпендикулярно поверхности, к площади этой поверхности (S ).
Вычислим силу (F ), с которой молекулы действуют на поршень:
1. Определим силу удара одной молекулы о стенку сосуда.
Пусть молекула идеального газа массой движется в плоскости XOY со скоростью и, ударившись о поршень, отскакивает от него со скоростью (см. Рис. 2). Согласно второму закону Ньютона, сила, действующая на молекулу со стороны поршня во время удара, равна:
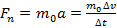 ,
,где a - ускорение молекулы при ударе; - изменение скорости движения молекулы при ударе; - продолжительность удара.
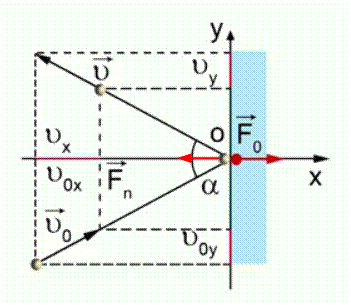
Рис. 2. Столкновение молекулы с поршнем
Проекция скорости на ось OY не изменяется, поэтому всё изменение скорости равно изменению скорости вдоль оси X :
Согласно третьему закону Ньютона, сила, с которой молекула действует на поршень, равна по модулю силе , с которой поршень действует на молекулу. Следовательно:
2. Рассчитаем число молекул N , ударившихся о поршень за интервал .
За интервал времени до поршня успеют долететь только те молекулы, которые движутся в направлении поршня и удалены от него на расстояние (см. Рис. 3). То есть фактически половина числа молекул, заключённых в цилиндре объёмом
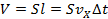 . Следовательно, число молекул, ударившихся о поршень за интервал , равно:
. Следовательно, число молекул, ударившихся о поршень за интервал , равно:Общее число молекул, которое равно произведению концентрации на объём:
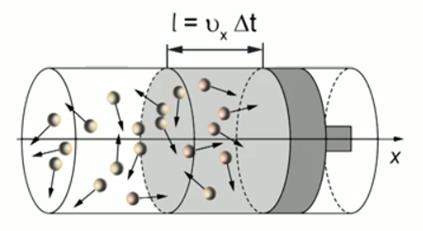
Рис. 3. Молекулы, ударившиеся о поршень за время
3. Определим общую силу ударов молекул о поршень.
Эта сила будет равна произведению силы удара одной молекулы на общее число ударов:
Мы живём в трёхмерном мире, то есть любая молекула имеет проекцию скорости . Так как все молекулы двигаются хаотично, то направления их движения равноправные, поэтому можно написать, что в среднем, для средней квадратичной скорости, одинаковые (). Следовательно, заменяем квадрат проекции скорости на средний квадрат проекции скорости:
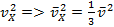
Подставляем это значение в формулу силы ударов молекул о поршень:
Значение данной силы подставим в формулу давления:
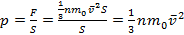
- основное уравнение МКТ идеального газа ,
- давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема
На данном уроке мы вывели основное уравнение МКТ. Обращаться к данному уравнению мы будем нечасто, так как удобнее работать с отдельными макропараметрами (проще отдельно измерить давление, объём, температуру, чем замерять скорость и массу конкретной молекулы). Тем не менее, именно это уравнение назвали основным, потому что оно даёт связь между макромиром и микромиром.
Список литературы
Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. - М.: Просвещение, 2008.
Физика. Тесты. 10-11 классы: учебно-методическое пособие / Н.К. Гладышева, И.И. Нурминский, А.И. Нурминский и др. - М.: Дрофа, 2005
Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. - М.: Илекса, 2005.
Касьянов В.А. Физика 10 класс. - М.: Дрофа, 2010.
- Easy-physic.ru ().
- Clck.ru ().
- Clck.ru ().
Домашнее задание
Тема: Основы молекулярно-кинетической теории
Урок: Основное уравнение молекулярно-кинетической теорииИзучение любой области физики всегда начинается с введения некой модели, в рамках которой идет изучение в дальнейшем. Например, когда мы изучали кинематику, моделью тела была материальная точка, когда изучали планетарные движения, планеты принимались за сферы и т. д. Как вы уже догадались, модель никогда не будет соответствовать реально происходящим процессам, но часто она очень сильно приближается к этому соответствию.
Молекулярная физика, и в частности МКТ, не является исключением. Над проблемой описания модели работали многие учёные, начиная с восемнадцатого века: М. Ломоносов, Д. Джоуль, Р. Клаузиус (Рис. 1). Последний, собственно, и ввёл в 1857 году модель идеального газа.

() () () Рис. 1. Джеймс Джоуль, Михаил Ломоносов, Рудольф Клаузиус соответственно
Определение. Идеальный газ - модель газа, в рамках которого молекулы и атомы газа представлены в виде очень маленьких (исчезающих размеров) упругих шариков, которые не взаимодействуют друг с другом (без непосредственного контакта), а только сталкиваются (см. Рис. 2).
Следует отметить, что разреженный водород (под очень маленьким давлением) практически полностью удовлетворяет модели идеального газа.
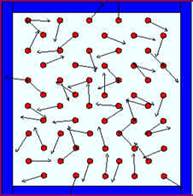
Теперь можно приступить к описанию параметров идеального газа. Они делятся на две группы:
Параметры идеального газа

То есть микропараметры описывают состояние отдельно взятой частицы (микротела), а макропараметры - состояние всей порции газа (макротела). Запишем теперь соотношение, связывающее одни параметры с другими, или же основное уравнение МКТ:
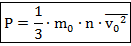
Здесь: - средняя скорость движения частиц;
Определение. - концентрация частиц газа - количество частиц, приходящихся на единицу объёма; ; единица измерения - .
Таким образом, основное уравнение МКТ вводит нам прямо пропорциональную зависимость макропараметра давления от микропараметров массы молекулы и средней скорости движения в квадрате. То есть чем тяжелее частицы и чем больше их скорости, тем сильнее они врезаются в стенки сосуда и тем большее оказывают давление.
Возможны и другие формы записи этого уравнения, если вспомнить некоторые формулы из более ранних разделов физики:
Средняя кинетическая энергия поступательного движения
Источник)
- Почему с увеличением массы молекул увеличивается давление?
- Почему модель идеального газа не соответствует действительности?
- Воздух состоит в основном из азота и кислорода. Концентрация какого газа больше?
- *Почему, говоря о микропараметрах идеального газа, мы указываем только кинетическую энергию молекулы и не указываем потенциальную?



