Уравнение менделеева клапейрона для смеси. Уравнение Менделеева-Клапейрона. Основное уравнение молекулярно-кинетической теории газов
Из уравнения состояния идеального газа p 1 V 1 / T 1 = p 2 V 2 / T 2 можно сделать вывод, что
для данной массы газа отношение произведения давле-ния газа на его объем к абсолютной тем-пературе газа является величиной постоянной:
pV / T = const.
Установлено, что для 1 моля газа эта константа равняется 8,31 Дж / (моль. К). Она называется универсальной газовой постоянной и обозначается буквой R. Следовательно, урав-нение состояния идеального газа для 1 моля газа можно записать в виде:
pV M = RT,
где V M — объем 1 моля газа, или молярный объем .
Это уравнение состояния иде-ального газа называется урав-нением Клапейрона в честь французского физика, который впервые его вывел.
Известный русский ученый Д. И. Менделеев вывел уравнение состояния для произволь-ного количества газа. Учитывая, что объем произвольной массы газа V = vV M = (m / M) . V M , где v — количество вещества, m — масса газа, M — его молярная масса, уравнение состоя-ния идеального газа можно записать в более общем виде:
pV = (m / M) . RT.
В таком виде оно называется уравнением Менделеева-Клапейрона . Все газовые зако-ны, открытые экспериментальным путем, можно вывести из этого уравнения как следствие, считая постоянным один из мак-ропараметров. Материал с сайта
Если учесть, что плотность газа ρ = m / V , то уравнение Менделеева-Клапейрона будет иметь вид:
p = (ρ / M) . RT.
Уравнение Менделеева-Кла-пейрона является общим урав-нением состояния идеального газа для произвольной его массы.
На этой странице материал по темам:
Физика закон менделеева и клапейрона
Физика формула менделеева вывести p
Закон клапейрона-менделеева формулировка
Как вывести уравнение менделеева-клапейрона
Вопросы по этому материалу:
Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т.
Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением
f (р, V, Т) =0,
где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон (1799-1864) вывел уравнение состояния идеального газа, объединив законы Бойля - Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V 1 , имеет давление р 1 и находится при температуре Т 1 . Эта же масса газа в другом произвольном состоянии характеризуется параметрами р 2 , V 2 , Т 2 (рис.63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1 -1 "), 2) изохорного (изохора 1 "-2).
В соответствии с законами Бойля - Мариотта (41.1) и Гей-Люссака (41.5) запишем:
p 1 V 1 =p " 1 V 2 , (42.1)
p " 1 /p " 2 =T 1 /T 2 . (42.2)
Исключив из уравнений (42.1) и (42.2) р" 1 , получим
p 1 V 1 /T 1 =p 2 V 2 / Т 2 .
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа
величина pV/T остается постоянной,
pV/T =B=const. (42.3)
Выражение (42.3) является уравнением Клапейрона, в котором В - газовая постоянная, различная для разных газов.
Русский ученый Д. И. Менделеев (1834-1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем V т . Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V m , поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению
pV m = RT (42.4)
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона - Менделеева.
Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях (р 0 = 1,013 10 5 Па, T 0 =273,15 K:, V m = 22,41 10 -3 м 3 /моль): R = 8,31 Дж/(моль К).
От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона - Менделеева для произвольной массы газа. Если при некоторых заданных давлений и температуре один моль газа занимает молярный объем l/m, то при тех же условиях масса т газа займет объем V = (m/M) V m , где М - молярная масса (масса одного моля вещества). Единица молярной массы - килограмм на моль (кг/моль). Уравнение Клапейрона - Менделеева для массы т газа
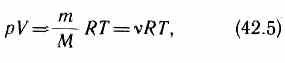
где v = m/M - количество вещества.
Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:
k=R/N А =1,38 10 -2 3 Дж/К.
Исходя из этого уравнение состояния (42.4) запишем в виде
p = RT/V m = kN A T/V m = nkT,
где N A /V m = n -концентрация молекул (число молекул в единице объема). Таким образом, из уравнения
p = nkT (42.6)
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м 3 газа при нормальных условиях, называется числом Лошмидта :
N L = P0 /(kT 0 ) = 2,68 10 25 м -3 .
Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р ,объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением: Рис.7.4.
F (p , V , T )=0,
где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля - Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V 1 , имеет давление р 1 и находится при температуре T 1 . Эта же масса газа в другом произвольном состоянии характеризуется параметрами р 2 , V 2 , Т 2 (рис.7.4).
Переход из состояния 1 в состояние 2осуществляется в виде двух процессов: 1) изотермического (изотерма 1 – 1 /), 2) изохорного (изохора 1 / – 2).
В соответствии с законами Бойля- Мариотта (7.1) и Гей-Люссака (7.5) запишем:
р 1 V 1 =p / 1 V 2 , (7.6)
. (7.7)
Исключив из уравнений (7.6) и (7.7) p / 1 получим:
.
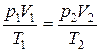Так как состояния 1 и 2были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.
pV/T = В = const. (7.8)
Выражение (7.8) является уравнением Клапейрона , в котором В - газовая постоянная, различная для разных газов.
Д. И. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (7.8) к одному молю, использовав молярный объем V m . Согласно закону Авогадро, при одинаковых p и Τ моли всех газов занимают одинаковый молярный объем V m ,поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной . Уравнению
pV m = RT (7.9)
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа , называемым также уравнением Клапейрона - Менделеева .
Числовое значение молярной газовой постоянной определим из формулы (7.9), полагая, что моль газа находится при нормальных условиях (р 0 = 1,013×10 5 Па, T 0 =273,15 К, V m =22,41×10 -3 м 3 /моль): R =8,31 Дж/(моль К).
От уравнения (7.9) для моля газа можно перейти к уравнению Клапейрона - Менделеева для произвольной массы газа. Если при некоторых заданных p и T один моль газа занимает молярный объем V m , то масса т газа займет объем V= (m/М ) V m ,где Μ – молярная масса (масса одного моля вещества). Единица молярной массы – килограмм на моль (кг/моль). Уравнение Клапейрона - Менделеева для массы т газа
pV = RT = vRT ,(7.10)
где: v=m/M - количество вещества.
Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана
k=R/N A = 1,38∙10 -23 Дж/К.
Исходя из этого, уравнение состояния (2.4) запишем в виде
p= RT/V m = kN A T/V m = nkT ,
где N A /V m =n - концентрация молекул (число молекул в единице объема). Таким образом, из уравнения
p=nkT (7.11)
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1м 3 газа при нормальных условиях, называется числом Лошмидта:
N l = р 0 / (kТ 0)= 2,68∙10 25 м -3 .
Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением
где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон (1799-1864) вывел уравнение состояния идеального газа, объединив законы Бойля - Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V 1 , имеет давление p 1 и находится при температуре T 1 . Эта же масса газа в другом произвольном состоянии характеризуется параметрами р 2 , V 2 , Т 2 (рис. 63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1 - 1¢, 2) изохорного (изохора 1¢ - 2).
В соответствии с законами Бойля - Мариотта (41.1) и Гей-Люссака (41.5) запишем:
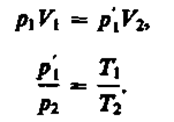(42.1) (42.2)
Исключив из уравнений (42.1) и (42.2) p¢ 1 , получим
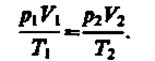
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.
Выражение (42.3) является уравнением Клапейрона, в котором В - газовая постоянная, различная для разных газов.
Русский ученый Д. И. Менделеев (1834-1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем V m . Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V m , поэтому постоянная B будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению
(42.4)
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона - Менделеева.
Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях (р 0 = 1,013×10 5 Па, T 0 = 273,15 К, V m = 22,41×10 -3 м э /моль): R = 8,31 Дж/(моль×К).
От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона - Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем V m , то при тех же условиях масса m газа займет объем V= (т/М)× V m , где М - молярная масса (масса одного моля вещества). Единица молярной массы - килограмм на моль (кг/моль). Уравнение Клапейрона - Менделеева для массы т газа
(42.5)
где v=m/M - количество вещества.
Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:
Исходя из этого уравнение состояния (42.4) запишем в виде
где N A /V m = n- концентрация молекул (число молекул в единице объема). Таким образом, из уравнения
(42.6)
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м 3 газа при нормальных условиях, называется числом Лошмндта*:
Основное уравнение
Молекулярно-кинетической теории
Идеальных газов
Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одно атомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS (рис. 64) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс m 0 v - (- т 0 ) = 2т 0 v, где m 0 - масса молекулы, v - ее скорость. За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой vDt (рис. 64). Число этих молекул равно nDSvDt (n- концентрация молекул).
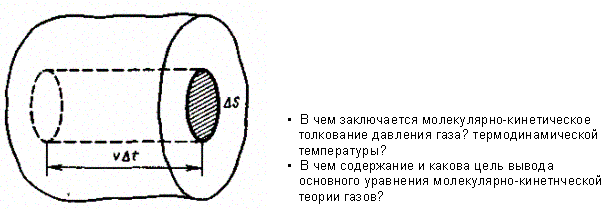
Необходимо, однако, учитывать, что реально молекулы движутся к площадке DS под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул - 1/6 - движется вдоль данного направления в одну сторону, половина - в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку DS будет
l / 6 nDSvDt. При столкновении с площадкой эти молекулы передадут ей импульс
Тогда давление газа, оказываемое им на стенку сосуда,
Если газ в объеме V содержит N молекул, движущихся со скоростями v 1 ,v 2 , ..., v n , то целесообразно рассматривать среднюю квадратичную скорость
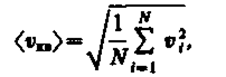(43.2)
характеризующую всю совокупность молекул таза. Уравнение (43.1) с учетом (43.2) примет вид
(43.3)
Выражение (43.3) называется основным уравнением молекулярно-кинетнческой теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.
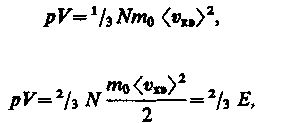(43.4) (43.5)
Учитывая, что n=N/V, получим
где Е - суммарная кинетическая энергия поступательного движения всех молекул газа.
Так как масса газа m=Nm 0 , то уравнение (43.4) можно переписать в виде
Для одного моля газа т = М (М - молярная масса), поэтому
где F m - молярный объем. С другой стороны, по уравнению Клапейрона - Менделеева, pV m = RT. Таким образом,
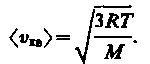(43.6)
Так как M = m 0 N A - масса одной молекулы, а N А - постоянная Авогадро, то из уравнения (43.6) следует, что
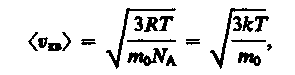(43.7)
где k=R/N A - постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода - 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
(использовали формулы (43.5) и (43.7)) пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения следует, что при Т=0
Если рассматривать некоторое количество газа, то эмпирически получено, что давление (), объем () и температура () полностью характеризуют эту массу газа как термодинамическую систему, если данный газ можно представить в виде совокупности нейтральных молекул, не имеющих дипольных моментов. В состоянии термодинамического равновесия связаны между собой уравнением состояния.
ОПРЕДЕЛЕНИЕ
Уравнение состояния газа в виде:
(где — газа; — молярная масса газа; Дж/Моль К — универсальная газовая постоянная; температура воздуха в Кельвинах: ) было впервые получено Менделеевым.
Его легко получить из уравнения Клапейpона:
учитывая, что в соответствии с законом Авогадро один моль любого газа при нормальных условиях занимает объем л. При этом получается, что:
Уравнение (1) называют уравнением Менделеева-Клапейpона. Иногда его записывают как:
где — количество вещества (число молей газа).
Уравнение Менделеева-Клапейpона получено на основе установленных эмпирически газовых законов. Так же как и газовые законы, уравнение Менделеева-Клапейpона является приближенным. Для разных газов границы применимости данного уравнения различны. Например, для гелия уравнение (1) справедливо в более широком диапазоне температур, чем для углекислого газа. Абсолютно точным уравнение Менделеева-Клапейpона является для идеального газа. Особенностью которого, является то, что его внутренняя энергия пропорциональна абсолютной температуре и не зависит от объема, который газ занимает.
Примеры решения задач
ПРИМЕР 1
| Задание | Температуру воздуха в комнате повысили от до Как при таких условиях изменится плотность воздуха в помещении ()? Тепловым расширением стен пренебречь. |
| Решение | Если тепловым расширением стен можно пренебречь, то объем комнаты не изменяется. В том, случае, если воздух нагревается при постоянном объеме давление должно расти с увеличением температуры, при этом его плотность не изменяется. Однако комната не является герметичной, поэтому объем газа (воздуха) в помещении постоянным считать нельзя. Постоянным в нашем случае является давление, которое равно наружному давлению атмосферы. При увеличении температуры уменьшается масса воздуха в комнате, так как газ выходит через щели наружу.
Вычислить плотность воздуха, можно используя уравнение Менделеева-Клапейpона:
Разделим правую и левую части уравнения (1.1) на V, имеем:
Из уравнения (1.2) выразим (), получаем:
Из выражения (1.3) видно, что при постоянном плотность обратно пропорциональна температуре для одного и того же газа, значит: |
| Ответ |
