Работа сторонних сил формула. Сторонние электродвижущие силы

Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока называются сторонними силами.

Электродвижущая сила

Скалярная физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС) , действующей в цепи или на ее участке:.

Напряжение

Напряжение – это физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи.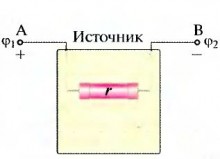

Разность потенциалов

Напряжение на неоднородном участке цепи (где есть сторонние силы) равно сумме ЭДС источника и разности потенциалов на этом участке:

Для однородного участка цепи , где сторонние силы не действуют,

Т.е. напряжение совпадает с разностью потенциалов на концах участка цепи .

Закон Ома для однородного участка цепи в интегральной и дифференциальной форме . Сопротивление и его зависимость от температуры. Сверхпроводимость.

Закон Ома для однородного участка цепи в интегральной и дифференциальной форме

Закон Ома для однородного участка цепи: н емецкий физик Георг Ом экспериментально установил, чтосила тока в цепи прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:.

Закон Ома в дифференциальной форме (закон Ома для плотности тока). Закон Ома в форме относится ко всему проводнику. Представим закон Ома в дифференциальной (т.е. относящейся к элементу тока длиныdl ) форме. Некоторая точка внутри проводника характеризуется вектором плотности тока , напряженностью электрического поляи свойствами материала проводника, т.е. удельным сопротивлением. Выделим мысленно малый объем вблизи рассматриваемой точки и подставимв закон Ома, получим:, здесь - разность потенциалов между сечениямиdS отстоящими на расстоянии dl . Следовательно,.

Учтем, что - напряженность электростатического поля;- плотность электрического поля;- удельная электрическая проводимость.

Тогда из формулы (20) следует закон Ома в дифференциальной форме : .

Сопротивление и его зависимость от температуры

Температурная зависимость сопротивления может быть представлена в виде:,

Сверхпроводимость

Сверхпроводимость – свойство некоторых проводников, заключающееся в том, что их электрическое сопротивление скачкомпадает до нуля при охлаждении ниже определенной критической температуры T к, характерной для данного проводника.

16. Работа и мощность тока. Закон Джоуля – Ленца в интегральной и дифференциальной форме

При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt . Электрическое поле на выделенном учестке совершает работу

выражающей закон Ома для однородного участка цепи с сопротивлением R , умножить на I Δt , то получится соотношение

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем иЭ. Ленцем и носит название закона Джоуля–Ленца .

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt , за которое эта работа была совершена:

Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).

Закон Джоуля-Ленца в дифференциальной форме - удельная мощность тока равна скалярному произведению векторов плотности тока и напряженности электрического поля:

,

где s - удельная проводимость;

r - удельное сопротивление среды.

Закон Джоуля-Ленца в дифференциальной форме носит совершенно общий характер, т. е. не зависит от природы сил, возбуждающих электрический ток. Закон Джоуля-Ленца, как показывает опыт, справедлив и для электролитов и для полупроводников.

17. . Обобщенный закон Ома для неоднородного участка цепи в интегральной и дифференциальной форме. Анализ обобщенного закона Ома. Замкнутая электрическая цепь. Соединение сопротивлений: последовательное и параллельное.

Если на концах какого-нибудь провод-ника AB создать разность потенциалов (рис. 5.16), то в нем возникнет электрическое поле напряженностью E̅.

Под действием этого поля свободные за-ряженные частицы (в металлах — это сво-бодные электроны) будут двигаться в опре-деленном направлении, не прекращая сво-его хаотического движения, создавая кратко-временный ток.

Тем не менее, на практике в подавляющем большинстве случаев необходимо иметь ток в проводниках на протяжении продолжитель-ного времени. Для этого на концах провод-ника разность потенциалов необходимо под-держивать неизменной. Эту функцию в элект-рических цепях выполняют источники тока.

Любой источник тока имеет два полюса: положительный и отрицательный. Источ-ник, как и любой другой проводник, имеет свое сопротивление r, которое называется внутренним сопротивлением (рис. 5.17).

На полюсах источника на протяжении продолжительного времени существует раз-ность потенциалов. Но почему же в таком случае не возникает ток в самом источнике? В самом деле, на полюсах батареи для кар-манного фонарика довольно долго сущест-вует разность потенциалов, однако ток воз-никает лишь тогда, когда к полюсам бата-реи подсоединяется лампочка. Очевидно, что в источнике существуют какие-то силы, ко-торые стараются поддерживать разность потен-циалов на его полюсах, противодействуют электрическим силам, стремящимся выров-нять потенциалы на полюсах источника. Эти силы имеют неэлектрическое происхожде-ние, поэтому и называются сторонними.

Рис. 5.17. Источник тока

Сторонние силы обусловливают разде-ление разноименно заряженных частиц в источнике и поддерживают на его полюсах определенную разность потенциалов. В галь-ванических элементах разделение заряжен-ных частиц осуществляется за счет хими-ческой энергии, в термогенераторах — за счет тепловой и т.п.

Таким образом, сторонние силы внутри источника тока создают электрическое по-ле, которое называется полем сторонних сил . Напряженность такого поля E ст. может измеряться силой, действующей на заря-женные частицы с суммарным зарядом в одну единицу. Материал с сайта

E ст. = F ст. / q.

Очевидно, что напряженности поля сто-ронних сил и электрических сил в источнике имеют противоположные направ-ления. Если внешняя часть цепи источника разомкнута, то напряженности обоих полей в источнике одинаковы и никакого тока в источнике нет.

Когда внешняя часть цепи ис-точника разомкнута, то напря-женность поля сторонних сил и электрических сил в источнике одинаковы по значению и про-тивоположны по направлению, поэтому и компенсируют друг друга.

Таким образом, роль источника сводится к разделению разноименно заряженных ча-стиц и к накоплению их на полюсах источ-ника.

1

11 Сторонние электродвижущие силы. Закон Джоуля - Ленца

Согласно (11.4), э.д.с. численно равна работе сторонних сил, совершаемой при перемещении единичного положительного заряда по замкнутой цепи.

Помимо сторонних сил, на заряд действуют силы электростатического поля, имеющего напряжённость 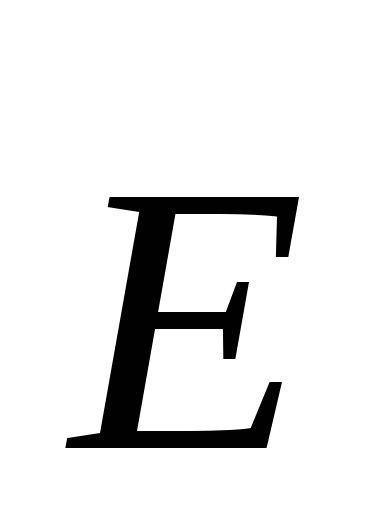. Следовательно, результирующая сила 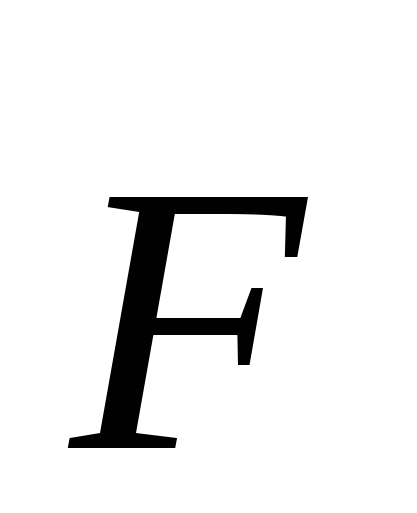, действующая на заряд 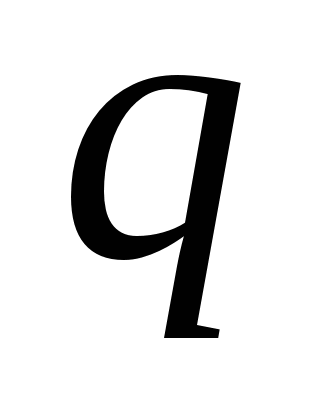в любой точке цепи, может быть записана в виде Данное правило Кирхгофа является условием стационарности токов. В противном случае потенциал рассматриваемого узла изменялся бы с течением времени, и это привело бы к изменению токов в цепи.

Второе правило Кирхгофа гласит, что алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на сопротивления этих участков равна алгебраической сумме э.д.с., действующих в этом контуре: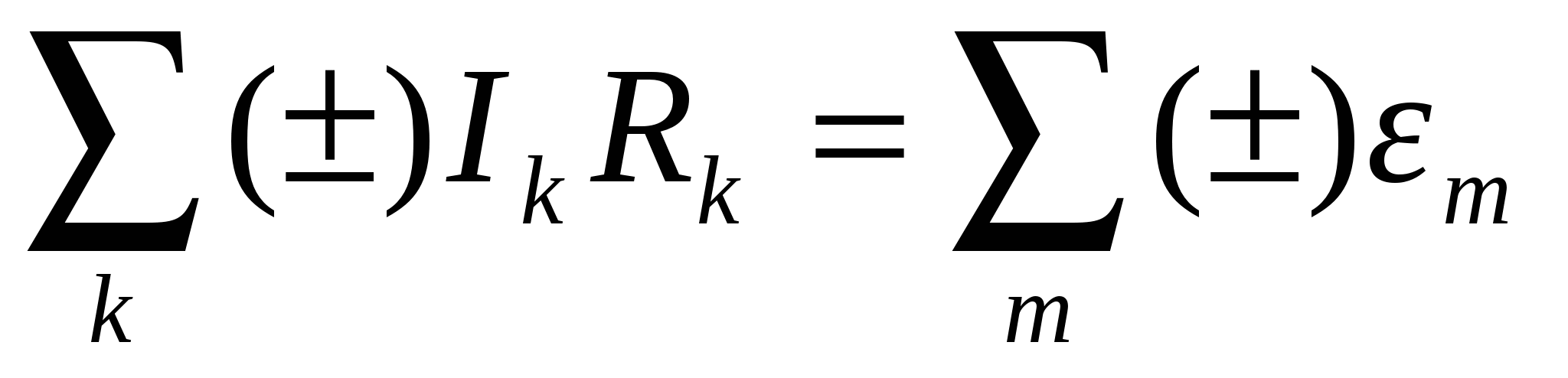


. (11.13)
Здесь 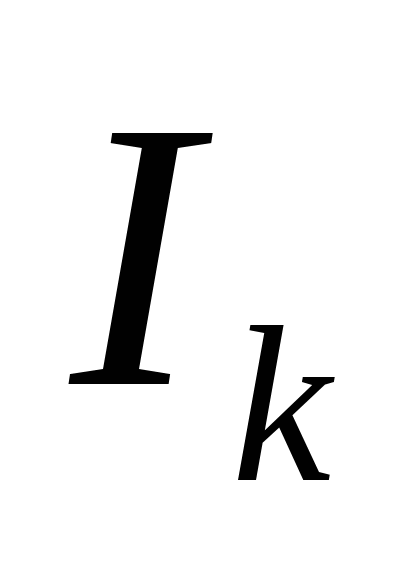и 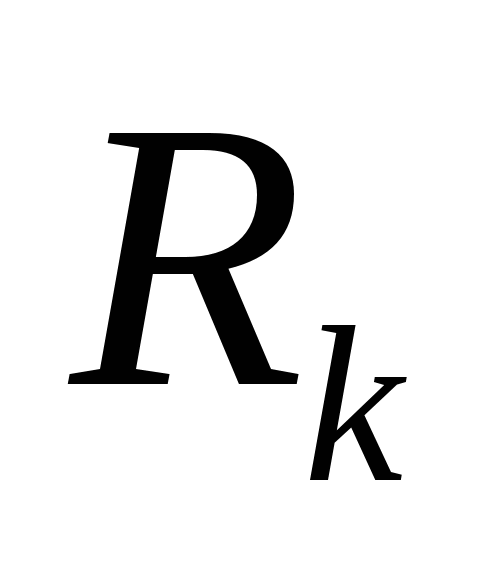- сила тока и сопротивление для некоторого участка замкнутой цепи, 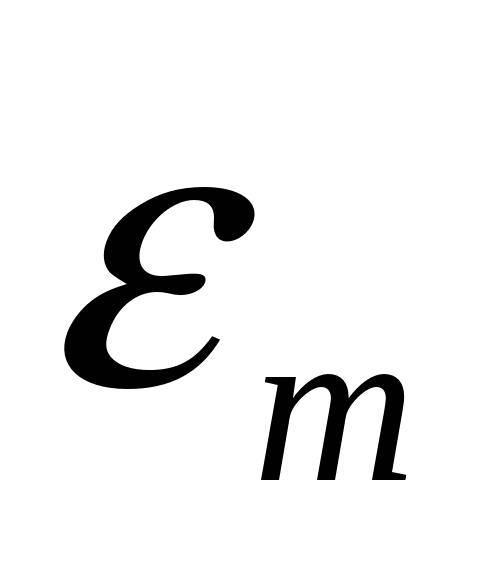- значение э.д.с. в этой же цепи.

Второе правило Кирхгофа является следствием закона Ома для замкнутой цепи. Направление обхода замкнутого контура и направление токов на всех участках цепи выбирают произвольным образом. Сила тока записывается со знаком "+", если его направление совпадает с направлением обхода замкнутого контура, и со знаком "-" в противоположном случае. Значение э.д.с. записывается со знаком "+", если при обходе замкнутого контура движение внутри источника осуществляется от его отрицательного полюса к положительному, то есть совпадает по направлению с внутренним током источника.

Для нахождения всех неизвестных токов необходимо решить систему независимых уравнений, в которой число уравнений должно быть равно числу неизвестных токов. В результате решения системы уравнений могут быть получены отрицательные значения силы тока. Это означает, что на рассматриваемом участке цепи реальный ток проходит в противоположном направлении относительно выбранного направления.

Например, в цепи, показанной на рисунке 16, можно выделить три замкнутых контура, для которых второе правило Кирхгофа имеет вид

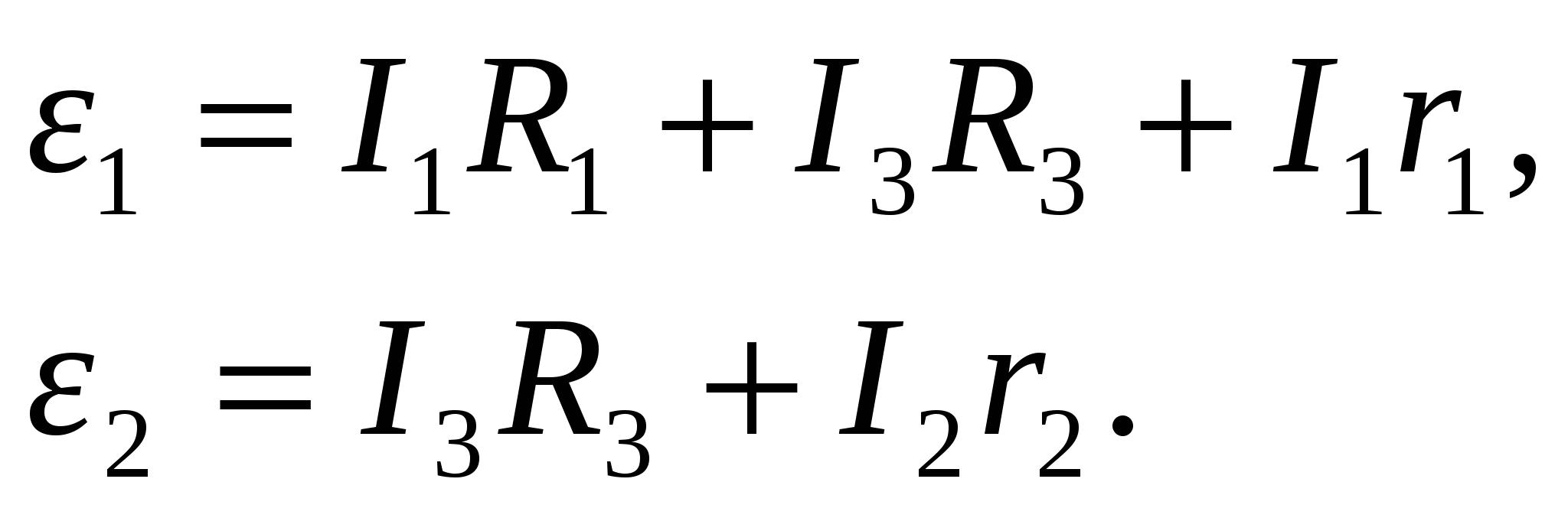(11.14)

Здесь первое уравнение записано для контура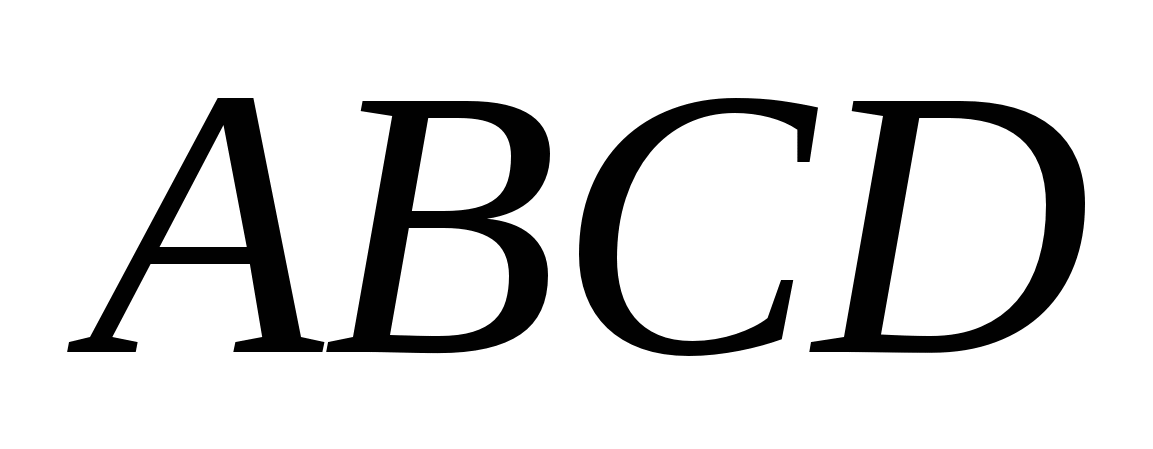

, второе уравнение – для контура

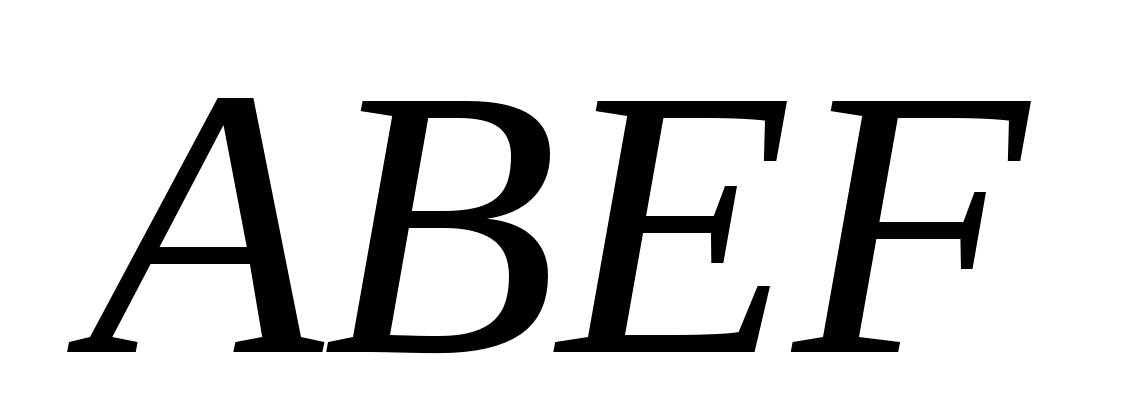, третье уравнение – для контура

. Данная система уравнений является линейно зависимой. Поэтому для вычисления неизвестных токов I 1 , I 2 , I 3 необходимо использовать любые два из этих трёх уравнений совместно с первым правилом Кирхгофа (11.12).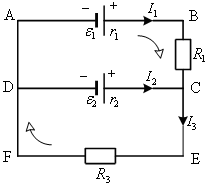

Рисунок 16 - Пример разветвлённой цепи постоянного тока
С помощью правил Кирхгофа можно рассчитать , например, э.д.с. и внутреннее сопротивление аккумуляторной батареи. Допустим, батарея состоит из нескольких источников постоянного напряжения, количество источников равно

, э.д.с. каждого источника равна , внутреннее сопротивление равно 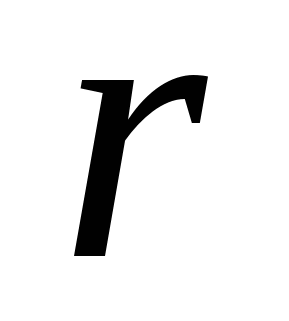, и источники соединены последовательно. Тогда общую э.д.с. и общее внутреннее сопротивление батареи можно вычислить следующим образом: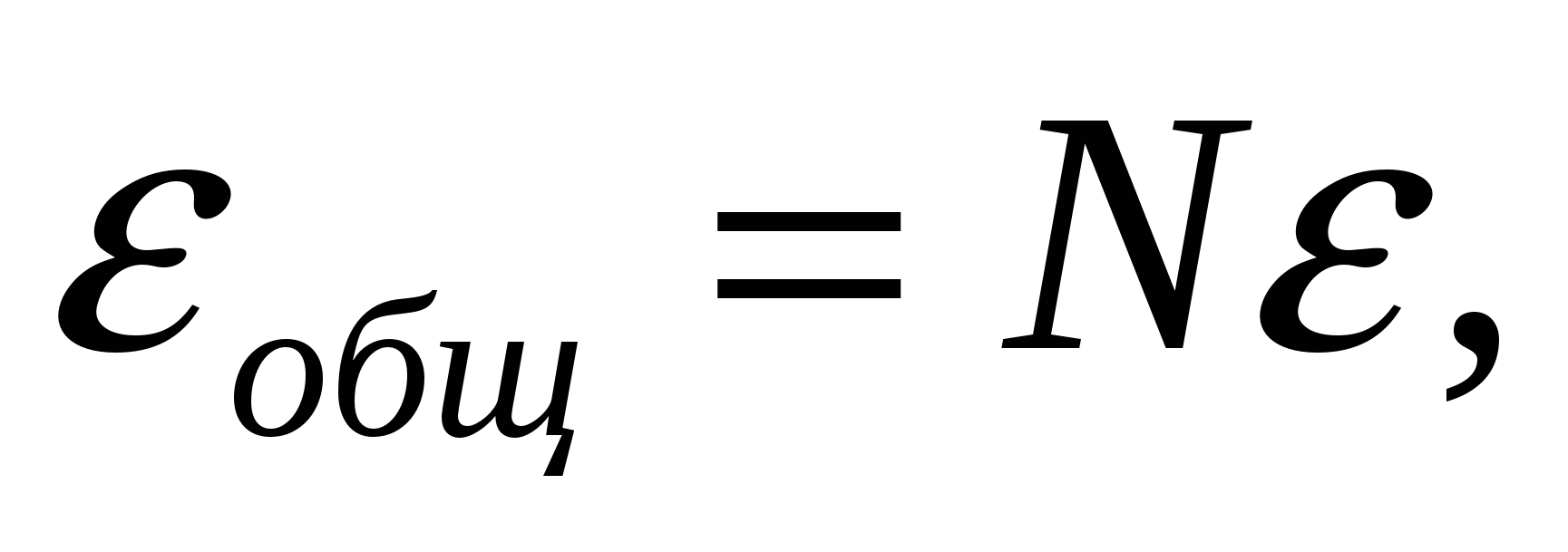



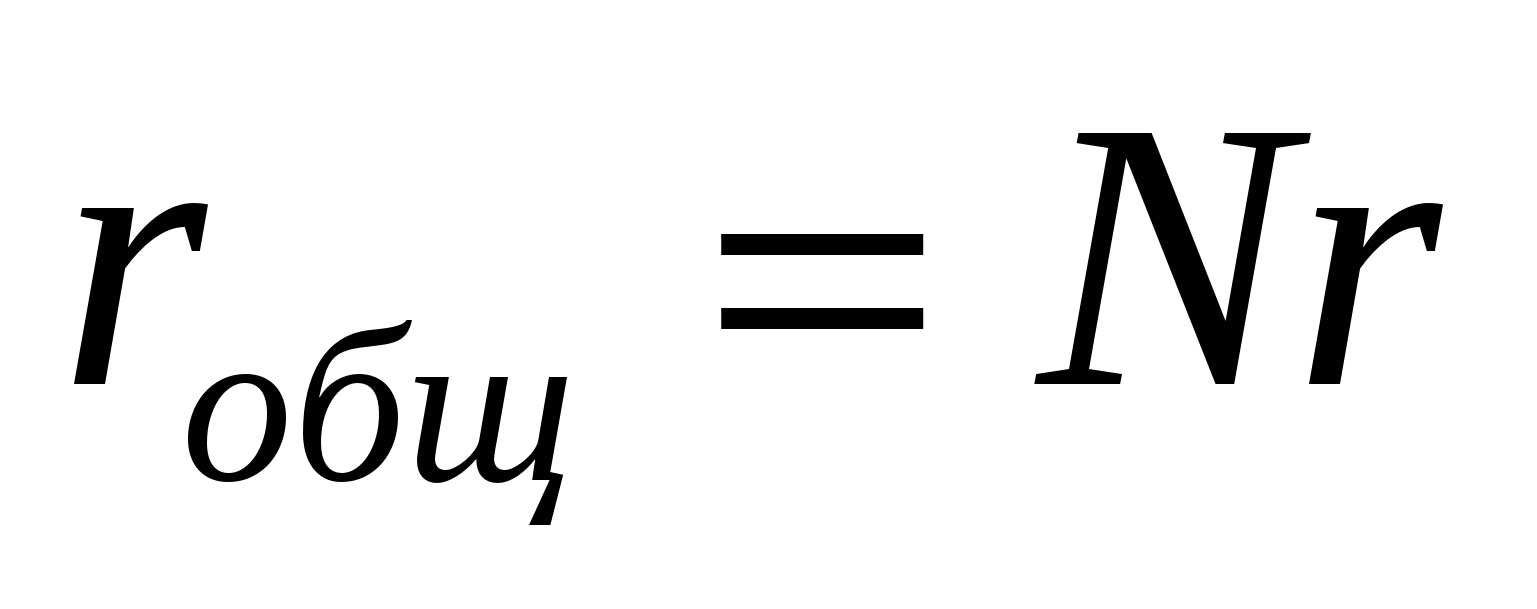. Если источники соединены в батарее параллельно, то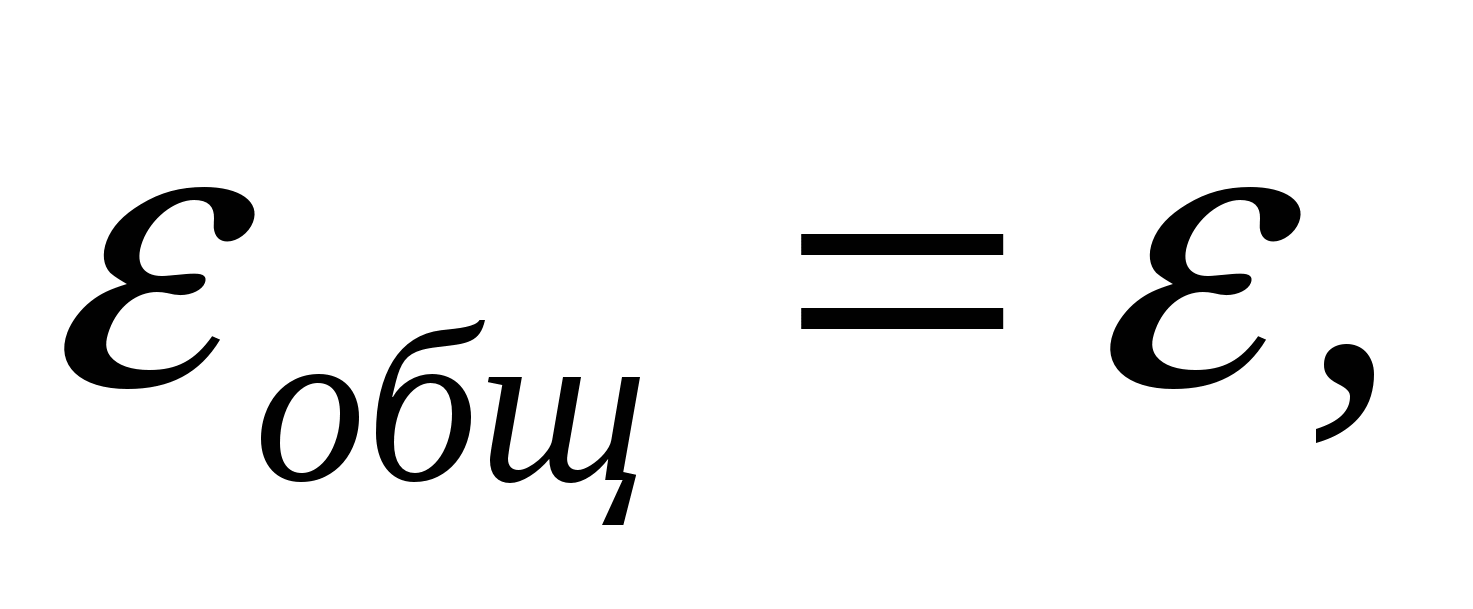



.

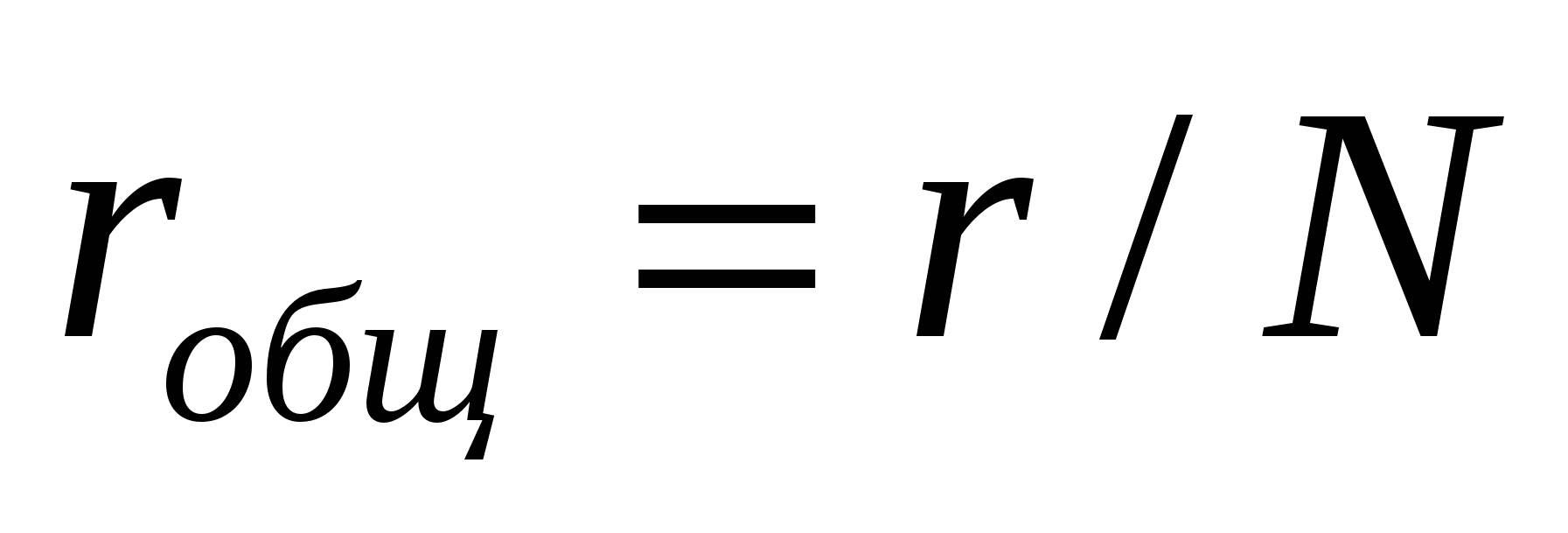При прохождении электрического тока в цепи выделяется тепло. Этот процесс можно характеризовать с помощью понятия о тепловой мощности тока

Тепловое действие тока можно описать на основании закона Джоуля - Ленца : тепловая мощность тока равна произведению силы тока 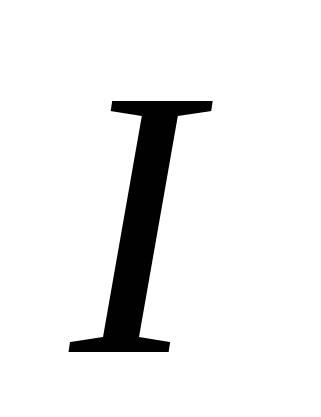на электрическое напряжение 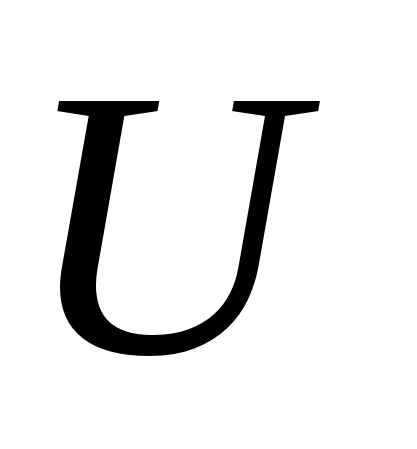на этом участке:


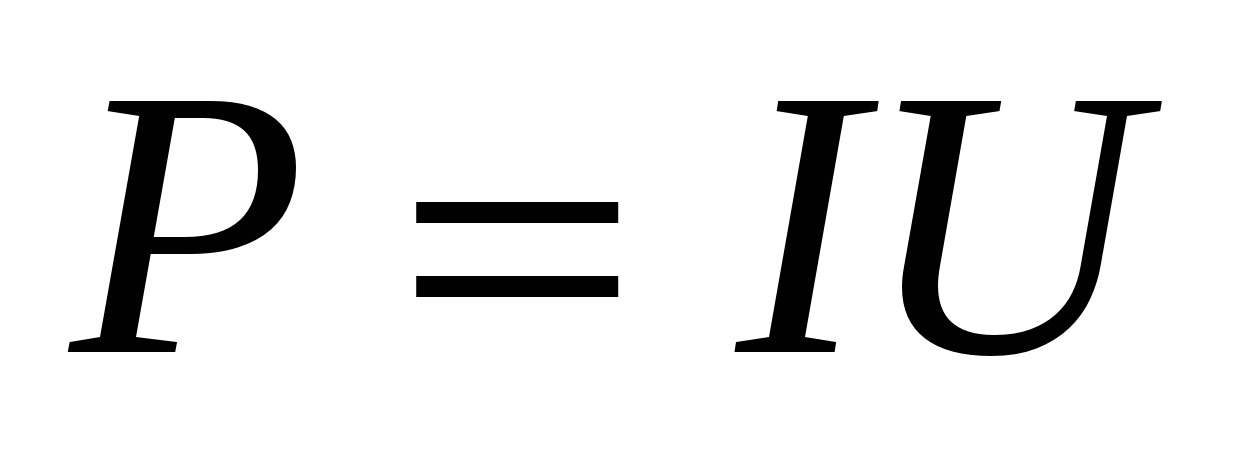. (11.16)
Используя закон Ома для участка цепи (10.10), выражение для тепловой мощности тока (11.16) можно представить в другой форме: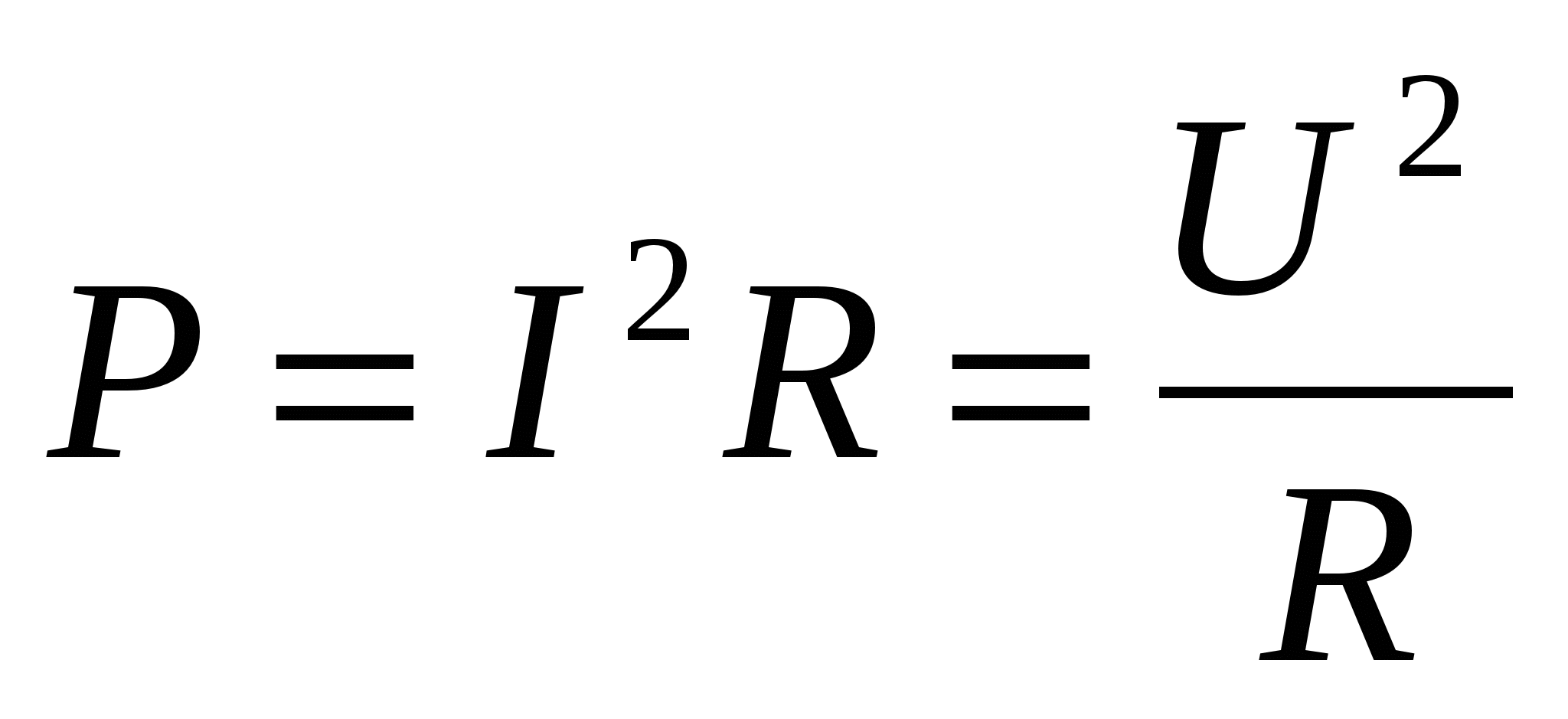


. (11.17)
Для переменного тока тепловая мощность зависит от времени. Если ток изменяется сравнительно медленно, его называют квазистационарным. Условие квазистационарности будет сформулировано в разделе 30. В этом случае количество выделяющейся теплоты можно вычислить следующим образом: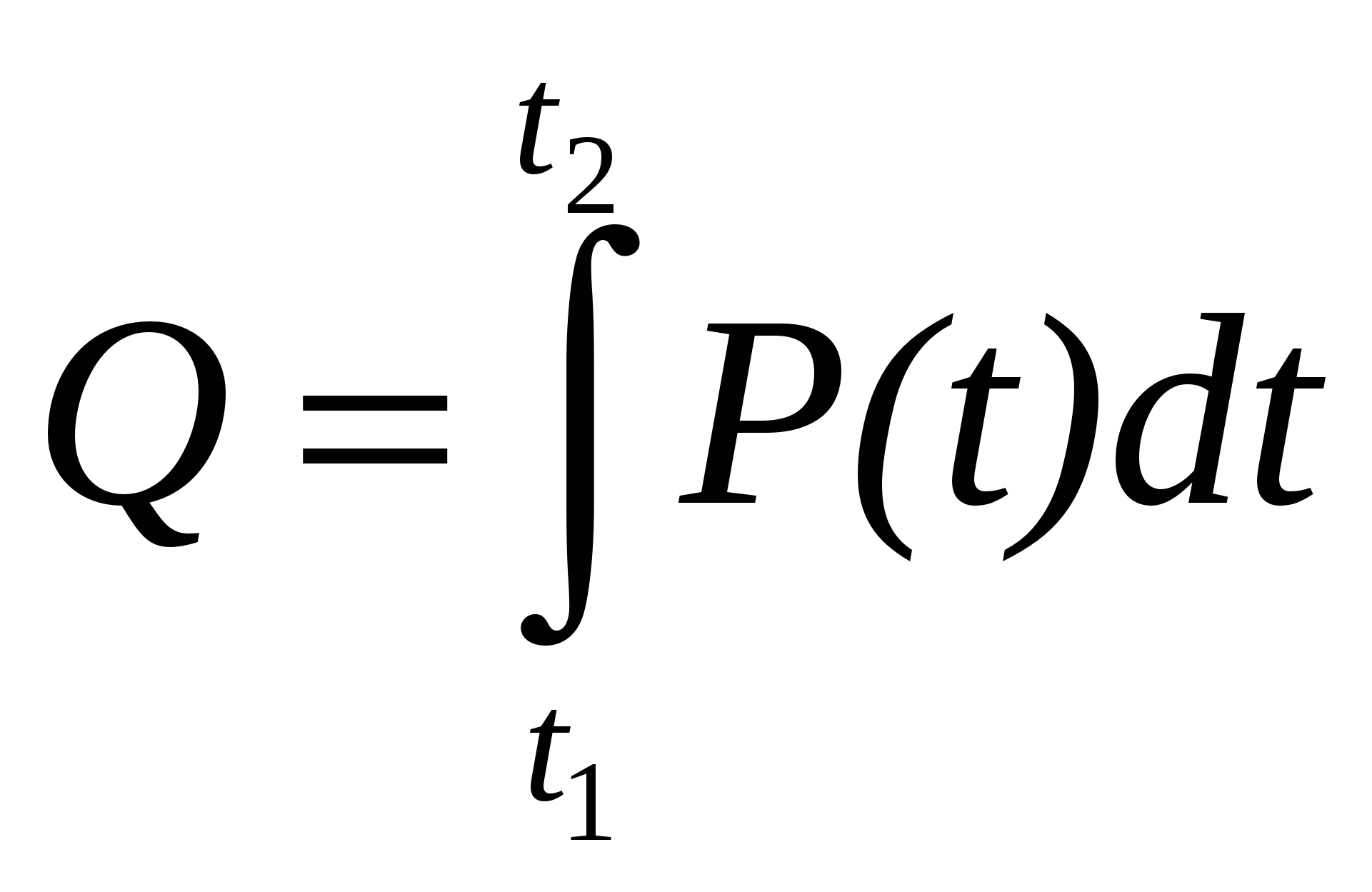


, (11.18)
где 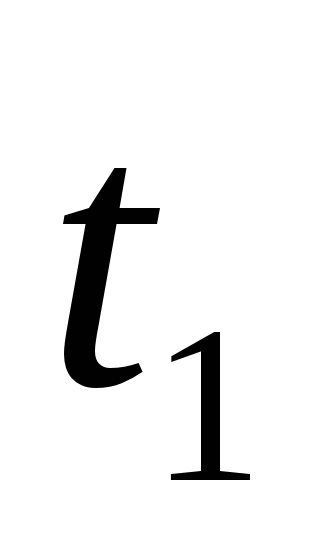и 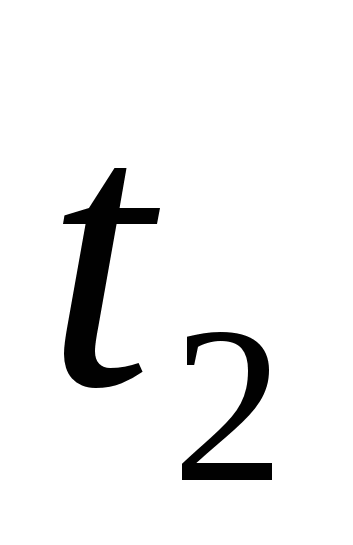- начальный и конечный моменты времени.

Для постоянного тока тепловая мощность не зависит от времени, и интеграл в выражении (11.18) следует заменить произведением мощности на длительность рассматриваемого промежутка времени.

Закон Джоуля – Ленца можно сформулировать также в дифференциальной форме. Для этого необходимо ввести в рассмотрение объёмную плотность тепловой мощности тока , то есть количество теплоты, выделяемой в единицу времени в единичном объеме проводника

Используя соотношение (11.16) и (11.19), получаем локальную формулировку закона Джоуля – Ленца: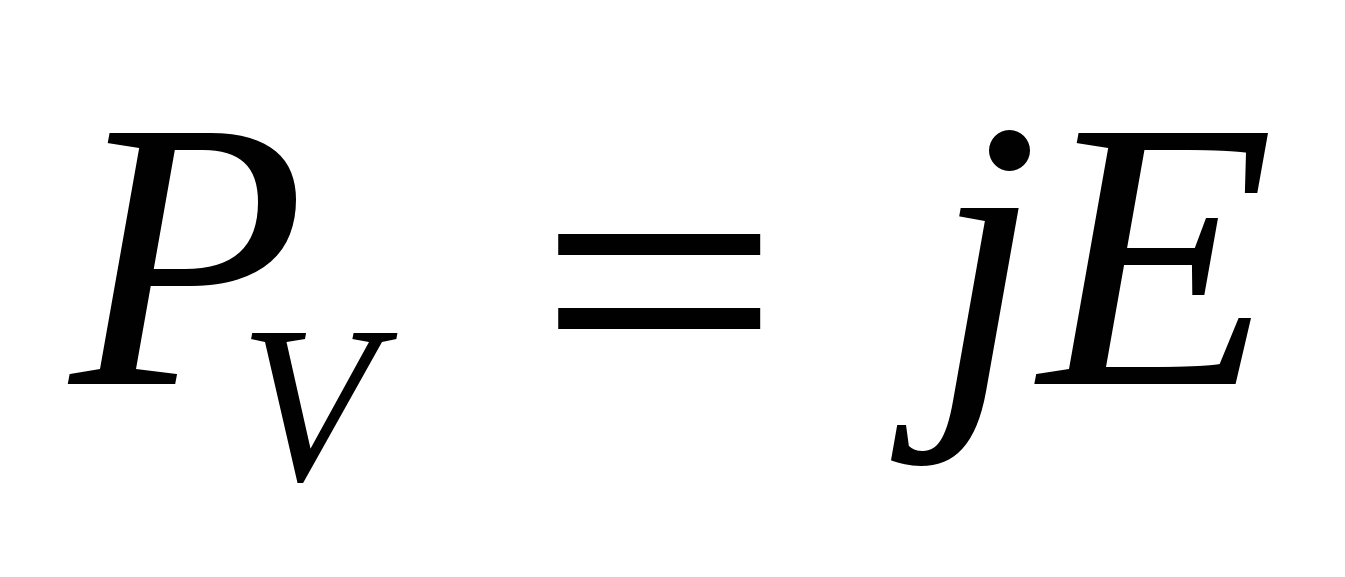


. (11.20)
Учитывая закон Ома (10.11), закон Джоуля – Ленца в дифференциальной форме можно записать также следующим образом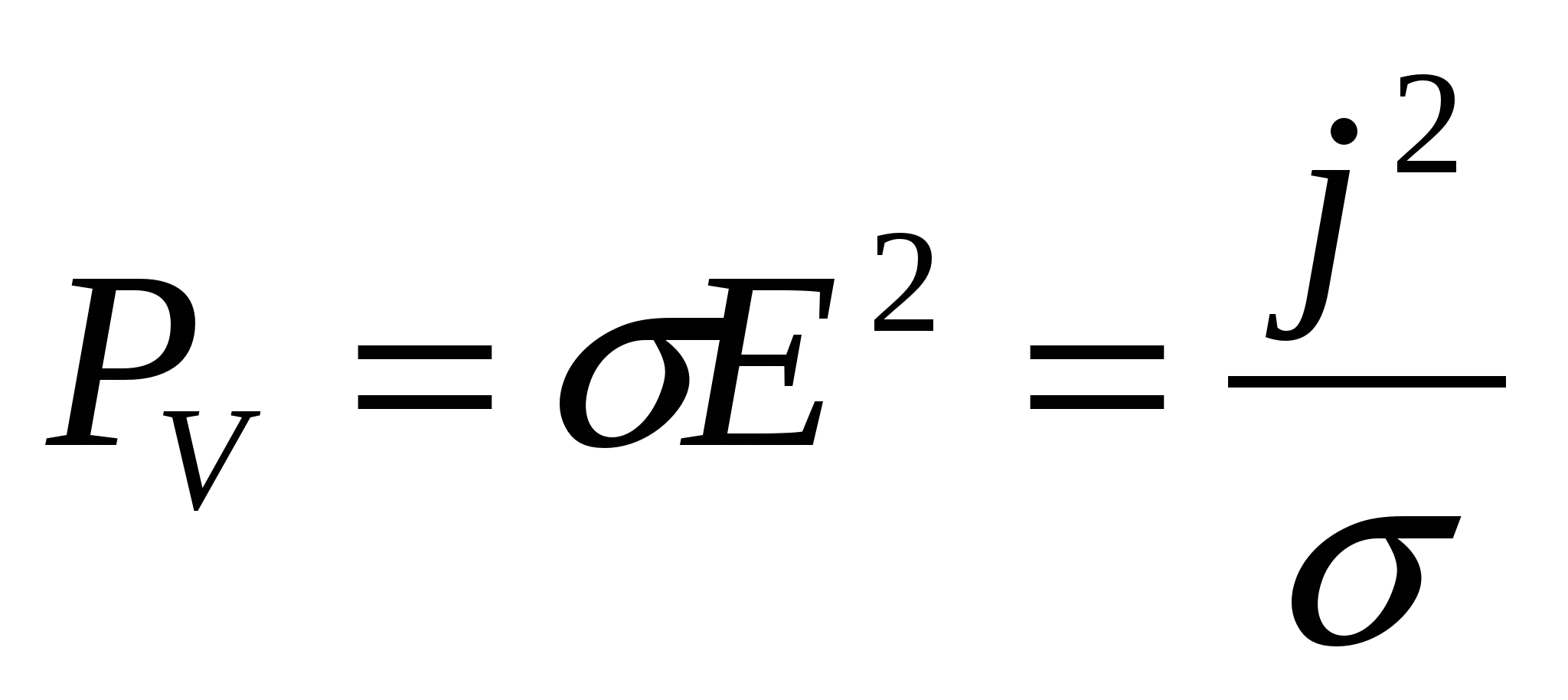


. (11.21)
Д ля выяснения физического смысла формулы (11.20) введём в рассмотрение объёмную плотность силы, действующей со стороны электрического поля на свободные заряды