Реальные источники создают сферические волны, но на большом расстоянии от источника малую часть фронта сферической волны можно считать плоской. Сферическую поверхность на небольшом участке тоже можно считать плоской. Поэтому наиболее простой случай отражения плоской волны от плоской границы раздела двух сред представляет практический интерес.

Электромагнитная волна, падая на границу раздела двух сред, частично отражается от нее, частично проходит в глубь второй среды. Поэтому в первой среде имеются падающая и отраженная волны, а во второй среде - преломленная волна. Часто бывает необходимо знать соотношение между составляющими поля E и H падающей и отраженной волн, например, при распространении радиоволн вблизи поверхности Земли.

Отражение радиоволн на границе раздела двух идеальных диэлектриков

При идеально ровной поверхности, согласно закону геометрической оптики, угол отражения равен углу падения θ, а угол преломления ψ связан с углом падения соотношением

где ε 1 и ε 2 - соответственно относительные диэлектрические проницаемости первой и второй среды.

Рассмотрим отдельно отражение вертикально- и горизонтально-поляризованных волн и найдем отношение комплексных амплитуд напряженностей электрического поля падающей E ⋅ m и отраженной E ⋅ 1m волн, называемое коэффициентом отражения:

R˜ = E ⋅ 1m / E ⋅ m = |R| e -jФ. (1.67)

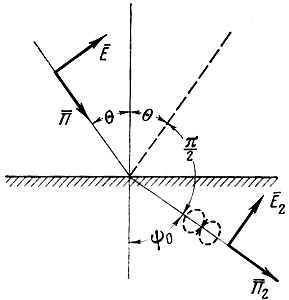
Вертикальная поляризация. На рис. 1.10 изображено отражение вертикально-поляризованной волны от границы раздела двух сред.

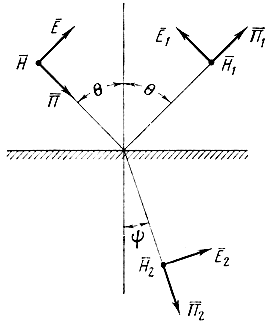
На границе раздела двух сред выполняются условия равенства тангенциальных составляющих векторов Е‾ и Н‾ . На основании этого граничного условия можно составить следующие уравнения (см. рис. 1.10):

E ⋅ m cos θ - E ⋅ 1m cos θ = E ⋅ 2m cos ψ; (1.68)

H ⋅ m + H ⋅ 1m = H ⋅ 2m .

Воспользовавшись соотношением между величинами E ⋅ и Н ⋅ [см. формулу (1.32)] и выразив угол ψ через угол θ, после преобразований получим

Проследим зависимость коэффициента отражения от угла падения волны на границу раздела двух сред для случаев, когда первая среда обладает меньшей или большей диэлектрической проницаемостью, чем вторая.

В первом случае (ε 1

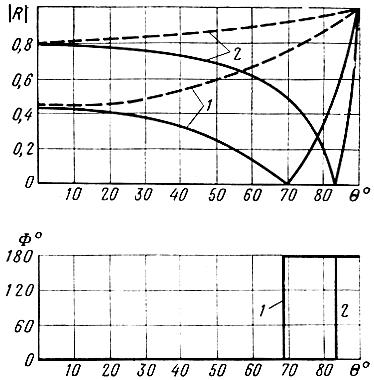
Рис. 1.11. Зависимости модуля и фазы коэффициента отражения от угла падения волны на границу раздела двух идеальных диэлектриков, когда ε 1

Из графиков видно, что при некотором значении угла θ = θ 0 отраженная волна отсутствует. При этом вся энергия падающей волны переходит во вторую среду. Угол θ 0 называется углом полного преломления. Величину угла θ 0 легко определить, приравняв числитель выражения (1.69) нулю, откуда

Во втором случае (ε 1 > ε 2) коэффициент отражения меняется от правильной отрицательной дроби (|R в |

Значение угла θ кр определяется выражением

При θ > θ кр вторые слагаемые в числителе и знаменателе уравнения (1.69) становятся мнимыми величинами, модуль коэффициента отражения остается равным единице, а фаза коэффициента отражения меняется от 0 до 180°. Явление, когда коэффициент отражения остается равным единице, называется полным внутренним отражением. Оно наблюдается, например, при отражении радиоволн от слоев ионосферы. Зависимость модуля и фазы коэффициента отражения от угла падения волны на границу раздела двух сред в этом случае изображена на рис. 1.12 сплошными линиями.

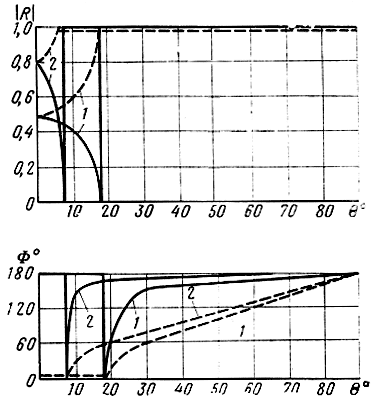
Рис. 1.12. Зависимости модуля и фазы коэффициента отражения от угла падения волны на границу раздела двух идеальных диэлектриков, когда ε 1 > ε 2: 1 - ε 1 = 10, ε 2 = 10; ε 2 = 1; 2 - ε 1 = 80, ε 2 = 1; ____ вертикальная поляризация; - - - горизонтальная поляризация

Горизонтальная поляризация. В случае горизонтальной поляризации граничные условия согласно рис. 1.13 запишутся так:

Е ⋅ m + Е ⋅ 1m = Е ⋅ 2m ; (1.72)

Н ⋅ m cos θ - H ⋅ 1m cos θ = H ⋅ 2m cos ψ.

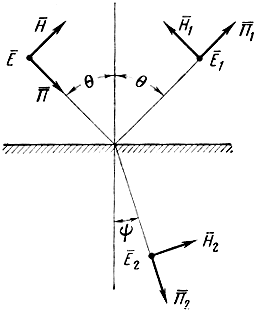
Используя соотношение (1.32) и проводя преобразования, получим выражение для коэффициента отражения горизонтально-поляризованной волны:

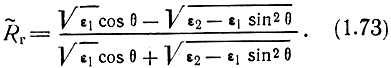
При горизонтальной поляризации зависимость коэффициента отражения от угла падения волны на границу раздела двух сред иная, чем при вертикальной поляризации.

Из анализа выражения (1.73) следует, что при ε 2 > ε 1 модуль коэффициента отражения меняется от правильной дроби при θ = 0 до |R г | = 1 при θ = 90°; фаза коэффициента отражения Ф г остается все время равной 180°. Эта зависимость изображена на рис. 1.11 пунктирными линиями.

Таким образом, явление полного отражения наблюдается как при горизонтальной, так и при вертикальной поляризации, если волна падает из более плотной среды в менее плотную.

Явление полного преломления не имеет места в случае горизонтальной поляризации. Это можно объяснить тем, что при прохождении волны во второй среде находящиеся в ней заряды колеблются в направлении вектора Е‾ этой волны (рис. 1.14).

Колеблющиеся заряды излучают, как элементарные электрические вибраторы, т. е. не излучают вдоль своей оси. Из (1.70) следует, что в случае вертикальной поляризации при θ = θ 0 направление ориентации осей вибраторов совпадает с направлением, в котором должна была бы распространяться отраженная волна.

Синус угла преломления оказывается при этом равным косинусу угла падения:

Следовательно, θ 0 + ψ 0 = 90° и в направлении 0О излучение отсутствует.

В случае горизонтальной поляризации вектор Е‾ при всех углах падения волны направлен параллельно границе раздела и нормально к плоскости падения волны. Поэтому направление ориентации осей вибраторов не может совпасть с направлением отраженной волны, и отраженная волна всегда существует.

Отражение радиоволн на границе раздела полупроводящих сред

Выражение для коэффициентов отражения радиоволн от полупроводящих сред получим путем замены в формулах (1.69) и (1.73) величины ε на комплексную величину ε˜. Величины R в И R г в этом случае являются также комплексными и их можно записать в виде

R в = |R в | е -jФ в, R г = |R г | е -jФ г, (1.75)

где Ф в и Ф г могут быть отличны от 0 и 180°.

При отражении от полупроводящей среды модуль и фаза коэффициента отражения зависит от частоты, так как величина ε˜ тоже зависит от частоты.

На рис. 1.15 представлены зависимости модуля и фазы коэффициента отражения, рассчитанные для случаев падения волн различной длины из среды с ε 1 = 1, γ = 0 на полу проводящую поверхность, для которой ε 2 > 1, γ ≠ 0. Сплошные кривые относятся к вертикальной, пунктирные - к горизонтальной поляризации.

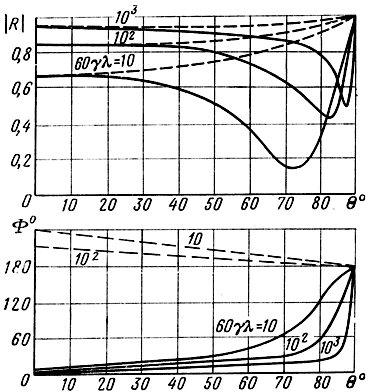
Рис. 1.15. Зависимости модуля и фазы коэффициента отражения от угла падения волны на границу раздела среды воздух - почва, когда ε 1 = 1, ε 2 = 10: ___ вертикальная поляризация; - - - горизонтальная поляризация

Из графиков видно, что для вертикальной поляризации характерно наличие минимума модуля коэффициента отражения, явления полного преломления в чистом виде не наблюдается. При горизонтальной поляризации кривые имеют монотонный характер, и для одних и тех же углов падения и длин волн коэффициент отражения выше, чем при вертикальной поляризации. С увеличением длины волны и электропроводности почвы модуль коэффициента отражения возрастает. Фаза коэффициента отражения при вертикальной поляризации резко изменяется и остается меньше или равной 180°. При горизонтальной поляризации фаза отраженной волны несколько больше или равна 180°.

Если поверхность идеально проводящая, то при любых углах падения волны происходит полное отражение и |R в | = |R г | = 1. Фаза отраженной волны при вертикальной поляризации Ф в = 0, а при горизонтальной Ф г = 180°, как следует из формул (1.69) и (1.73).

Для практического определения модуля и фазы коэффициента отражения служат специальные графики, представляющие собой зависимость R от угла падения волны на поверхность Земли .

Мгновенное значение напряженности электрического поля отраженной волны непосредственно над поверхностью Земли

E 1 = |R| Е m cos (ωt - Ф),

а на некотором расстоянии h над поверхностью Земли

Для определения напряженности электрического поля отраженной волны при произвольной линейной поляризации падающей волны необходимо прежде всего разложить вектор Е‾ на вертикальную и горизонтальную составляющие:

E ⋅ в = E ⋅ m cos ξ и E ⋅ г = E ⋅ m sin ξ,

где ξ - угол поляризации, т. е. угол между вектором E‾ и плоскостью падения волны.

Затем, используя известные коэффициенты отражения для каждой из этих составляющих, найдем составляющие напряженности электрического поля отраженной волны:

E ⋅ 1в = |R в | E ⋅ m cos ξ cos (ωt - Ф в);

E ⋅ 1г = |R г | E ⋅ m sin ξ cos (ωt - Ф г). (1.77)

Выражения (1.77) представляют собой уравнения эллипса. Следовательно, в общем случае отраженная волна поляризована эллиптически, т. е. конец вектора Е‾ за один период описывает эллипс, лежащий в плоскости, перпендикулярной к плоскости падения волны (рис. 1.16).

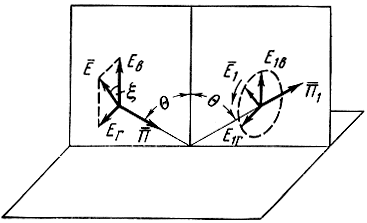
Когда поверхность является идеальным проводником или идеальным диэлектриком, разность фаз Ф в - Ф г равна нулю или 180° и волна остается линейно-поляризованной. При этом коэффициент отражения

Плоскость поляризации при отражении изменяется, и угол поляризации становится равным

Линейная поляризация отраженной волны получается также при угле падения, равном углу полного преломления. В этом случае в отраженной волне вертикальная составляющая напряженности поля отсутствует, и волна поляризована всегда горизонтально.

Вспомним, что в однородной среде свет распространяется прямолинейно. Это дает возможность при описании распространения света в такой среде пользоваться световыми лучами.

Изменение направления распространения света происходит на границе раздела двух различных сред. Поэтому, если установить из опытов законы, позволяющие точно определять такие изменения, то с помощью световых лучей можно описывать ход многих оптических явлений, не учитывая физической природы светового излучения. Часть оптики, в которой используется такой метод описания явлений, называют геометрической оптикой. В этой главе рассматриваются законы, которым подчиняются оптические явления, происходящие на границе раздела двух прозрачных сред.

Когда на поверхность воды из воздуха падает тонкий пучок света (рис. 29.1), то можно заметить, что в точке падения О часть света отражается, а часть проникает в водуи при этом преломляется. Вспомним, что углы и а соответственно называют углом падения и углом отражения (§ 24.19). Угол составленный преломленным лучом и перпендикуляром к поверхности раздела двух сред в точке падения лучей, называют углом преломления.

Возникает вопрос: сколько энергии, принесенной излучением на поверхность раздела двух сред, унесут отраженные лучи и сколько - преломленные? Пусть излучение приносит в точку О за некоторое время энергию Дальше эта энергия разделяется: одну ее часть уносят отраженные, а другую - преломленные лучи. Из закона сохранения энергии следует, что

Поскольку всякая среда (кроме вакуума) поглощает энергию излучения, это равенство справедливо только при измерении энергии вблизи точки О. Если световое излучение проходит в среде значительные расстояния, мало ослабляясь, то среду называют прозрачной (например, стекло, воду, спирт и т. п.). Напротив, металлы очень сильно поглощают проникающее в них световое излучение, т. е. непрозрачны для него. Большую часть падающего на них излучения они отражают.

Вспомним, что морская вода и другие электролиты - хорошие проводники электрического тока, но слабо поглощают видимое излучение и этим резко отличаются от металлов. Это объясняется тем, что в электролитах нет свободных электронов, а ионы из-за своей сравнительно большой массы не успевают следовать высокочастотным колебаниям в световом луче.

Итак, каждая среда в той или иной степени отражает и поглощает световое излучение. Отражение и поглощение падающего на тело излучения зависят от рода вещества, от состояния поверхности, от состава излучения, от угла падения лучей и других причин. При увеличении угла падения лучей доля отраженного света увеличивается, а проникающего - уменьшается.

Заметим, что зависимость отражения и поглощения от частоты колебаний чаще всего имеет избирательный характер, т. е. колебания с одной частотой вещество отражает или поглощает сильно, а с другой - слабо. Например, атмосфера Земли сильно поглощает короткие волны видимого спектра и значительно слабее - его длинные волны. (Подумайте, почему в качестве сигнала об опасности используется красный свет, хотя наибольшая чувствительность глаза относится к зеленым лучам.)

Основы оптики. Явления на границе раздела двух сред

При рассмотрении явления отражения электромагнитной волны от границ раздела сред могут иметь место три случая:

1) волна распространяется из среды менее плотной в среду более плотную и слабо поглощающую, т. е. n 1 < n 2

2) волна распространяется из среды более плотной в среду менее плотную n 1 > n 2 и коэффициент поглощения k 2  0;

3) имеет место падение излучения на границу раздела двух сред, из которых вторая менее плотная n 1 > n 2 и коэффициент поглощения k 2  0.

1. Отражение и пропускание на границе раздела двух сред при распространении из менее плотной среды в более плотную среду. Угол Брюстера.

Рассмотрим явления, соответствующие приведенным соотношениям. Отражение световой волны, происходящее на границе двух различных сред (при соотношении n 1  n 2 ), неразрывно связано с явление преломления луча во вторую среду. Если показатели преломления обоих сред одинаковы, то отражения не происходит даже в том слу­чае, когда среды различаются по другим свойствам. Законы отраже­ния принимают простой вид для случая оптически гладкой плоской поверхности раздела. При выполнении этого условия каждый луч падающего пучка света отражается так, что угол падения, образуемый лучом с нормалью к поверхности в точке его падения, равен углу от­ражения; причем оба луча (падающий и отраженный) лежат в одной плоскости с нормалью к поверхности. Эта плоскость называется плоскостью падения.

Основным свойством зеркально отраженной волны является ее когерентность с волной падающей и преломленной. При встрече падающей и отраженной волн образуются стоячая и бегущая волны и наблюдается интерференция. Частота световых колебаний при зеркальном отражении не меняется. Таким образом, отражение от диэлектриков дает возможность получить когерентные волны.

Законы отражения света, учитывающие состояние поляризации от­раженной и преломленной волн, выводятся для перечисленных выше случаев из общей теории отражения и преломления электромагнитных волн и представляются в виде формул Френеля.

Пусть имеются два диэлектрика, разделенных плоской поверхностью и характеризуемых показателями преломления n 1 и n 2 (диэлектрические проницаемости  1 и  2).

На поверхность раздела под углом α (рис. 5.1) падает линейно поляризованная волна. При падении на поверхность раздела она дает отраженную (угол отражения α) и преломленную (угол преломления β) волны. Все три луча лежат в одной плоскости - плоскости падения.

Для решения задачи об интенсивности и поляризации отраженной и преломленной волн нужно использовать условия на границе раздела для электрического и магнитного полей (векторы и

).

Падающую волну любого вида поляризации можно разложить на две составляющие, что показано на рис 5.3, а, б; вектор лежит в плоско­сти падения, вектор- перпендикулярен ей. Будем называть поляриза­цию в первом случае параллельной, а во втором - перпендикулярной.

Примем определенную систему для обозначения направлений коле­баний векторов и

, пусть переход от направления колебания векто­ра к направлению

будет происходить по часовой_стрелке при на­блюдении навстречу лучу. Положение векторов, и

обозначено на рис.5.1, а, б.

Формулы Френеля для амплитудных коэффициентов отражения и пропускания получены с учетом граничных условий, которые требуют непрерывности тангенциальных составляющих и

электромагнит­ной волны на границе раздела двух сред. Тогда для колебаний векторов, параллельных плоскости падения E II и E r , II , имеем для амплитудно­го коэффициента отражения

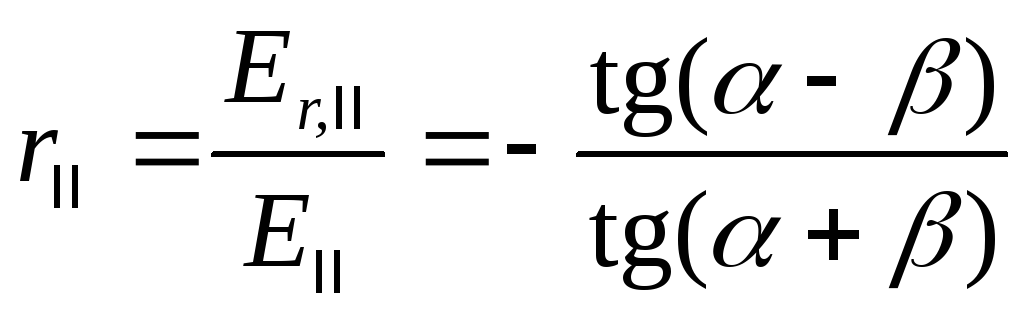(5.1)

Для колебаний векторов E ┴ и E r , ┴ , перпендикулярных плоскости падения, имеем

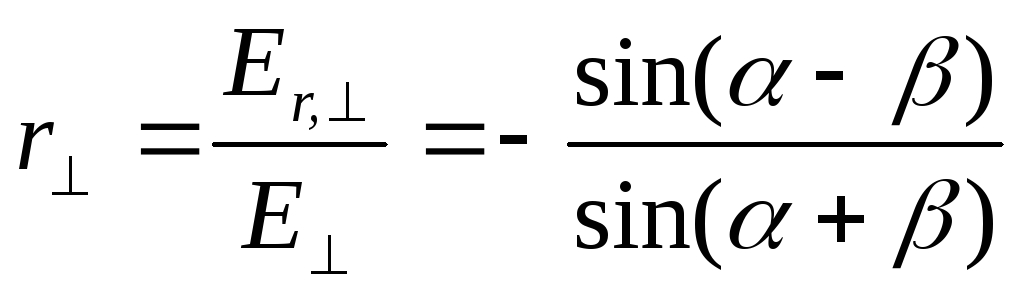(5.2)

Соответственно можно написать формулы для преломленных волн, поляризованных параллельно E t , II и перпендикулярно E t , ┴

(5.3)

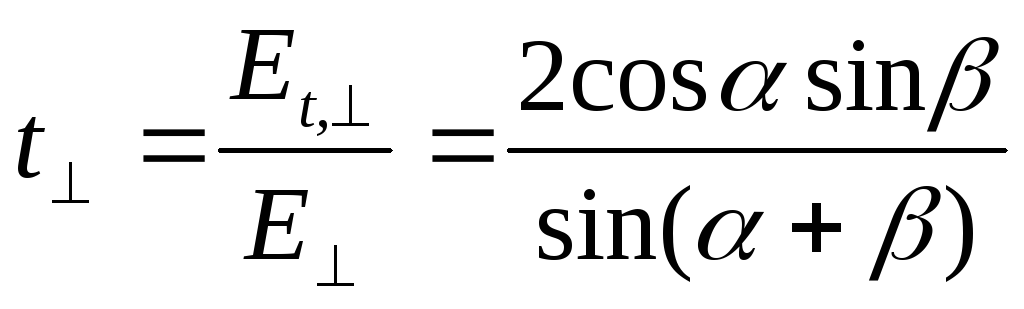(5.4)

Уравнения (5.1) - (5.4) известны как формулы Френеля. Они дают полное представление об амплитуде и фазе отраженной и пре­ломленной волн при прохождении света из менее плотной в более плотную непоглощающую среду. Графики зависимостей (5.1) - (5.4) при n 1 =1,0; n 2 =1,5 даны на рис.5.2, а.

Рассмотрим более подробно формулы (5.1) и (5.2). Они дают возможность построить кривые для амплитуд и фаз отраженных волн в зависимости от углов падения. При отражении света от более плот­ной среды для компонентыE r , II , имеет место скачок фазы колебаний по отношению к фазе падающей волны на π в определенных интервалах углов падения. Это подтверждается экспериментально.

Ориентация векторов и

в отраженной волне (с учетом сказанного выше) представлена на рис. 5.1, а, б. При такой ориентации для вектора

при отражении скачок фазы отсутствует, что и должно быть, так как на границе раздела магнитные свойства среды не меняются. На рис. 5.1 векторы в падающей и отраженной волне противоположны по фазе, что соответствует ориентации векторов, изображенной на рисунке.

При принятом выборе знаков в формулах (5.1) и (5.2) поворот плоскости поляризации в отраженной волне меняется монотонно, что иллюстрируется на рис. 5.3. Как видно из рисунка, в результате из­менения амплитудE r , II и E r , ┴ , отраженная волна с начальной ориентаци­ей вектора r под углом 45° к плоскости падения испытывает поворот плоскости поляризации при изменении угла падения α. При скользя­щем падении (α=90°) плоскость поляризации ориентирована под уг­лом 90° к исходной.

Из формулы (5.1) при α+β=π/2 следует, что коэффициент r II обращается в нуль. При одновременном присутствии в падающем из­лучении параллельной и перпендикулярной компонент отразится от поверхности раздела только компонента E r , ┴ и свет станет линейно по­ляризованным. При α+β=π/2 sin β = cos α (рис. 5.4) и инвариант преломления для относительного показателя преломления дает

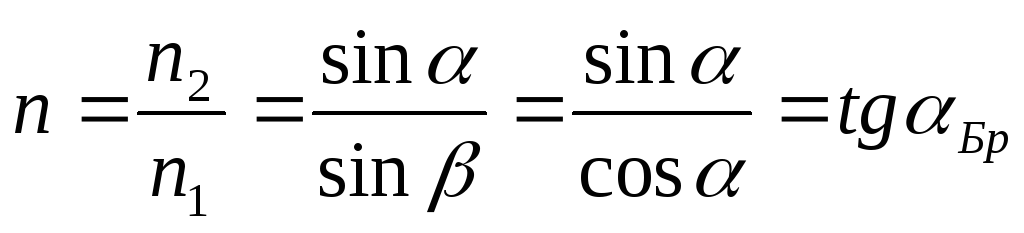. (5.5)

Угол, соответствующий условию (5.5), называют углом Брюстера для случая n =1,5 и =0,5 мкм α=57°. На рис. 5.2, б изобра­жен график изменения фазы между отраженной и падающей волнами для обеих поляризаций  II и  ┴ для всех углов α.

Рассмотрим подробнее зависимость от угла падения разности фаз  II и  ┴ между падающим и отраженным лучами. Из формулы (5.2) следует, что для всех углов 0<α<π/2 для перпендикулярной поляри­зации разность фаз  ┴ остается постоянной и равной π (см. рис.5.2, б). для параллельной поляризации разность фаз  II также равна π при таких значениях α, для которых, сумма α+β≤π/2. При α+β=π/2 в формуле (5.1) знак тангенса изменится и произойдет скачок фазы на π, т. е. фаза отраженной волны совпадает с фазой падающей. В соот­ветствии с формулой (5.1) амплитудный коэффициент отражения ме­няет знак.

Для реальной границы раздела скачкообразное изменение фазы  II при α = α Бр не наблюдается. На рис. 5.2, 6 пунктирной линией пока­зан реальный ход зависимости  II . Таким образом, в этом случае при α = α Бр мёжду параллельной и перпендикулярной компонентами имеется разность фаз, приближенно равная π/2.

Для прёломленной волны из формул (5.3) и (5.4) следует, что при любом значении углов падения α и преломления β зна­ки E II и E t , II , знаки E ┴ и E t , ┴ совпадают. Это свидетельствует о том, что преломленная волна во всех случаях имеет фазу падающей волны. Амплитудные же коэффициенты про­пускания t II и t ┴ (так же, как и в отраженной волне) отличаются и зависят от углов падения (см. рис. 5.2, а).

Покажем, что при падении линейно поляризованного света направ­ление плоскости поляризации в отраженной и преломленной волнах оказывается повернутым относительно соответствующего направления этой плоскости в падающей волне. Этот поворот происходит вследствие различной зависимости амплитудных коэффициентов отражения и пропускания волн разной поляризации от угла падения α. Обозначив азимуты колебаний электрического вектора в падающей, отраженной и преломленной волнах через γ, η, ε, можно записать:

,

,

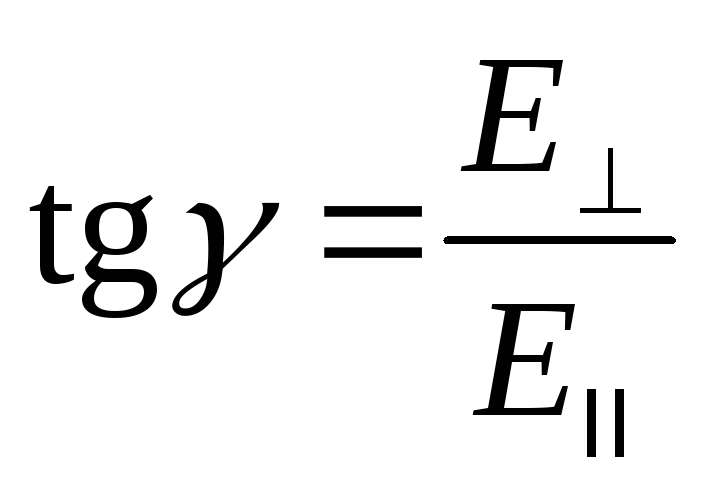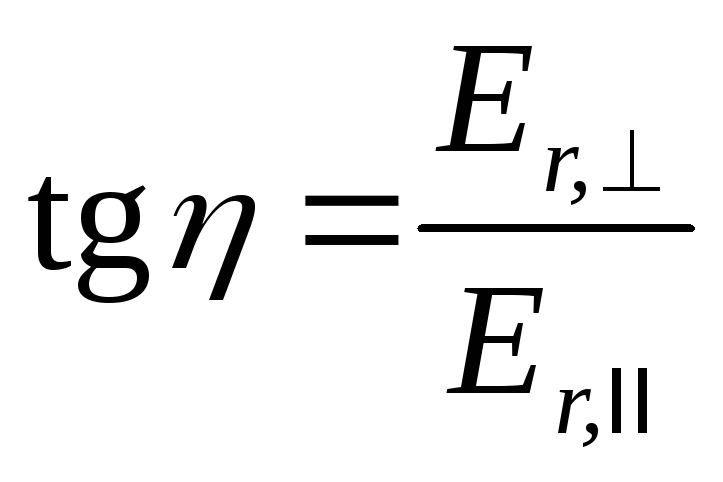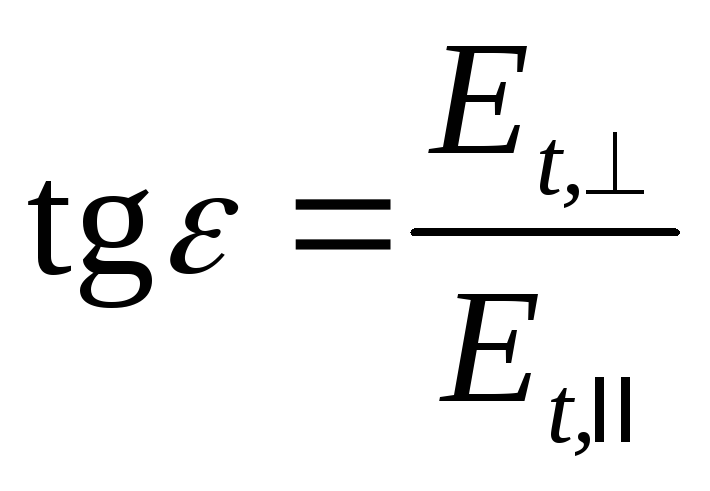
Отсюда с учетом (5.1) и (5.2), (5.3) и (5.4) имеем:

;

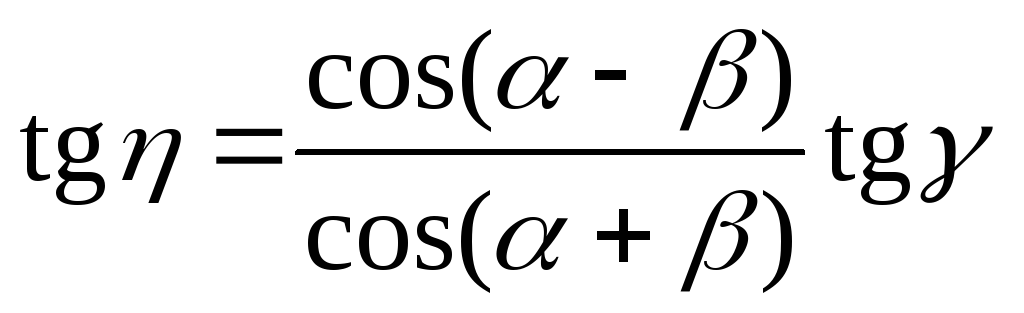Из этих формул следует, что при увеличении угла падения плос­кость колебаний в отраженной волне удаляется, а в преломленной вол­не приближается к плоскости падения. При угле падения, соответст­вующем углу Брюстера, tg η = ∞, т. е. η = π/2, а при углах α>α Бр имеем tg η < 0 вследствие изменения знака соs(α + β) и соответствующего скачка фазы для r II .

Если принять γ = 45°, то E II = E ┴ , и соответственно r II = r ┴ при α = 0. При увеличении угла α, в соответствии с формулами (5.1) и (5.2), r ┴ возрастает, а r II убывает и азимут и увеличивается. Когда α = α Бр, r II = 0 и η становится равным 90°. Затем знак r II изменяется и η становится больше 90°. При скользящем падении (α = 90°), r II = -r ┴ = 1 и угол и будет равен 135° или - 45°. Изменение η в зависимости от угла падения α представлено на рис. 5.3. Отметим еще угол падения α = 45°. В этом случае имеем по фор­мулам (5.1) и (5.2):

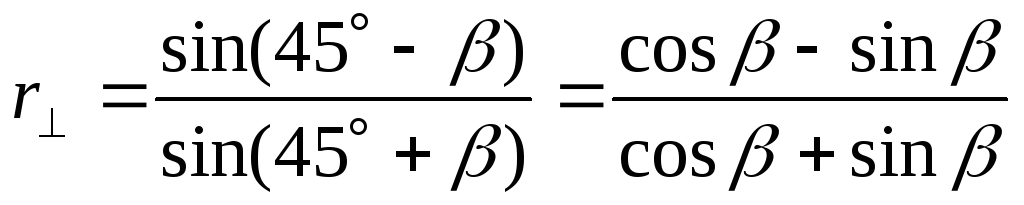
Следовательно, при α = 45° получим с учетом (5.6) соотношения:

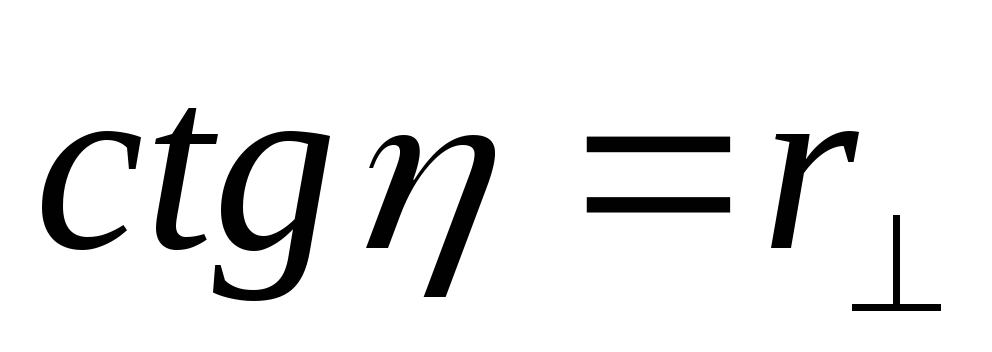, r ┴ 2 = r II (5.7)

Соотношения (5.7) позволяют определить амплитудные коэффи­циенты отражения по положению плоскости поляризации, не проводя фотометрических измерений.

Рассмотрим энергетические коэффициенты в отраженной и прелом­ленной волнах. Обозначим через R ┴ , R II , T ┴ , T II соответствующие состав­ляющие коэффициентов отражения и пропускания. Примем во внима­ние, что энергия поля падающей волны распределяется между энергиями полей отраженной и преломленной волн по-разному. Она зависит не только от коэффициентов отражения и пропускания границы раздела и от оптических характеристик сред n 1 и n 2 , но и от направления распространения волн (вектора Пойнтинга). Этим объясняется появление мно­жителя

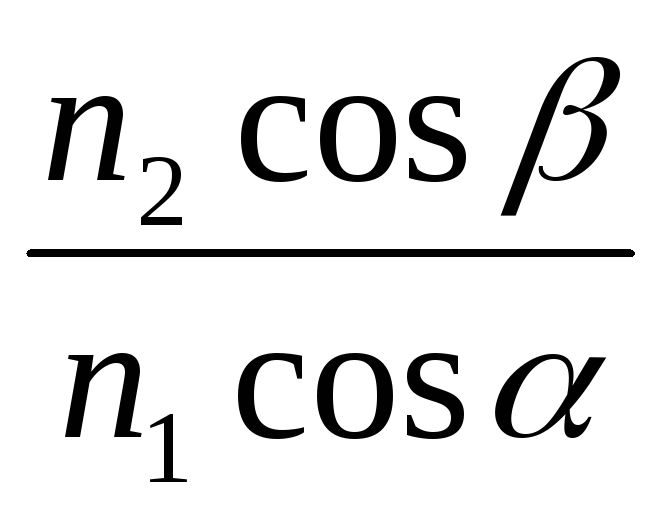в выражениях для составляющихT ┴ , T II .

Тогда имеем:

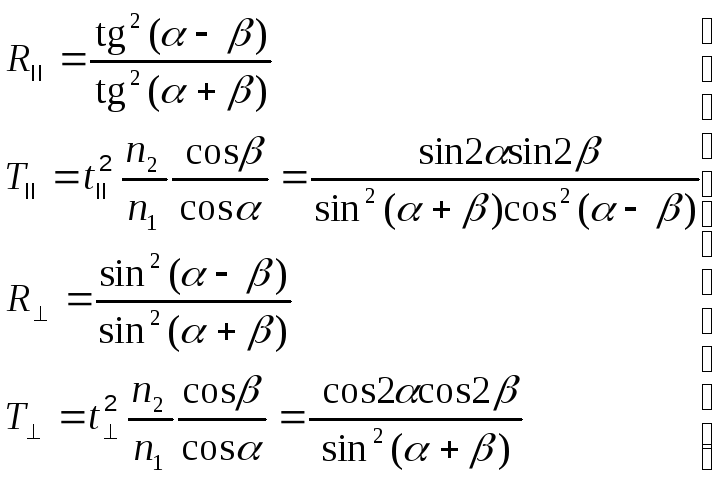(5.8)

Легко проверить, что в обоих случаях выполняется закон сохранения энергии, т. е.

R II + T II = 1 и R ┴ + T ┴ =1

Для неполяризованного света, когда имеет место осевая симметрия расположения вектора , средние значения то II 2 = ┴ 2 . Тогда энергетический коэффициент отражения будет равен полусумме квадратов амплитуд для параллельной и перпендикулярной компонент отраженной волны, т. е.

На рис. 5.5 представлены кривая коэффициента отраженияR для неполяризованного света и кривые для R ┴ и R II . Здесь рассмотрен случай отражения от границы воздух - стекло для n 2 = 1,52 (α Бр = 56°40’).

Из рис. 5.5 следует, что при α = α Бр в отраженном свете присутствует только одна поляризация. Коэффициент отражения неполяризованного света в этом случае R = R ┴ /2. Для α  α Бр в отраженном свете присутствуют обе поляризации. На рис.5.5 все три кривые для R , R ┴ , R II совпадают при α = 0 и α = 90°.

Наличие полностью поляризованного света при α = α Бр можно определить экспериментально (рис. 5.6).

На рисунке показан ход лучей при отражении от двух диэлектрических поверхностей S 1 и S 2 при α = α Бр. При повороте S 2 вокруг оси, совпадающей с лучом, интенсивность света на выходе меняется и при определенном положении становится равной нулю. В этом случае плоскости падения на зеркала S 1 и S 2 взаимно перпендикулярны.

Рассмотрим случай перпендикулярного падения волны на поверхность раздела. Напишем формулы Френеля (5.1) и (5.2) при условии, чтоα = 0 и β = 0. Для амплитудных коэффициентов отражения получаем

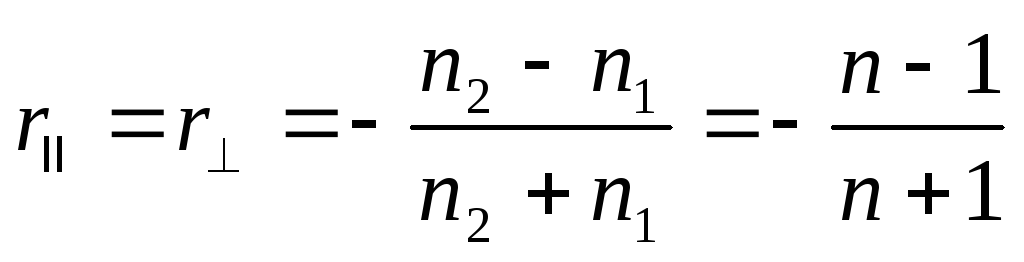, (5.10)

где n = n 2 /n 1 .

Из формулы (5.10) следует, что различие между параллельной и перпендикулярной поляризациями волн исчезает, и понятие плоскости падения теряет смысл.

Энергетический коэффициент отражения R при α = 0 получим возведением обеих частей равенства (5.10) в квадрат:

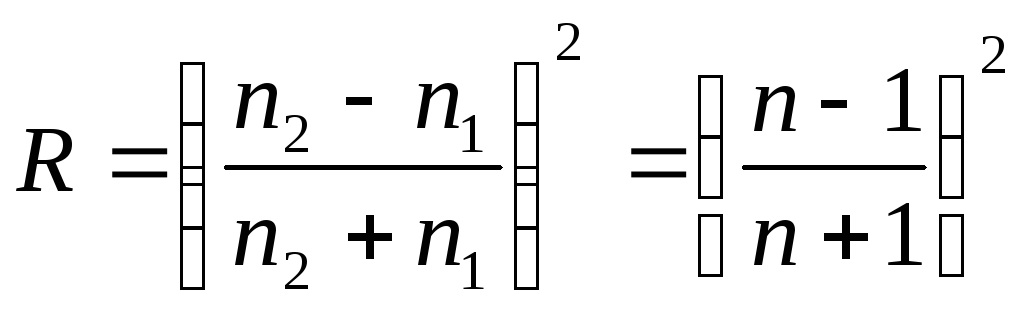. (5.11)

Для прозрачных диэлектриков величина R обычно мала. Например, для видимой области (зеленая длина волны) при n = 1,52 величина R = 0,04, т. е. 4% от падающего на поверхность света идет в отраженную волну. Необходимо отметить, что значение коэффициента отражения при нормальном падении не зависит от направления распространения луча, т. е. от того, из какой среды (первой или второй) свет падает на границу раздела. Таким образом, при прохождении волны через стеклянную пластинку теряется 8% энергии, т. е. коэффициент пропускания такой пластинки T = 92 %.

Если оптическая система состоит из многих поверхностей, то коэффициент пропускания Т может стать малым, для повышения пропускания необходимо осуществлять «просветление» элементов системы.

Из формулы (5.11) следует, что при уменьшении разницы между n 2 и n 1 коэффициент R заметно уменьшается. Например, при прочих равных условиях для границы стекло - вода (n отн = 1,33) коэффициент R = 0,019.

Из рис. 5.5 следует, что энергетический коэффициент отражения R увеличивается с увеличением угла падения α . Кроме того, изменяется также доля компонент R ┴ и R II . Свет оказывается частично поляризованным, так как