1.Общие свойства атомных ядер. Опытами Резерфорда было установлено существование атомных ядер. Атомном ядру каждого элемента, присущи определенные свойства, которые определяют: электрический заряд, массу, электрический и магнитный моменты, спин и т.д. Заряд ядра. Электрический заряд атомного ядра является положительным. Значение его определяется произведением Ze, где Z - атомный номер элемента равно порядковому номеру в периодической системе Д. И. Менделеева, е - элементарный заряд, равный 1,6022 1019Кл. Электрический заряд определяет число протонов в ядре и число электронов в нейтральном атоме, характер внутриатомного электрического поля, от которого зависят физические и химические свойства атомов. Масса ядра - это его второй важной характеристикой. Практически масса атомного ядра совпадает с массой атома, поскольку масса электронов, входящих в состав атома, очень незначительна. Массу атомов можно определить по отклонению их ионов в электрическом и магнитном полях. Атомы, ядра которых имеют одинаковые заряды, но отличаются массами, называют изотопами.

Размеры и форма ядер. Определенные сведения о размерах и форме ядра можно получить, изучая его электрическое поле, которое исследуют методом рассеяния заряженных частиц на ядрах. Исследование электрического поля ядра позволили сделать вывод и о его форме. Так, в случае сферически-симметричного ядра его поле должно быть также сферически-симметричным, то есть таким, как и поле точечного заряда. Проведенные исследования показали, что не все ядра является сферически-симметричными, но для всех ядер без исключения характерна осевая симметрия.

Спин ядра вместе с зарядом и массой является его важнейшей характеристикой. Спином ядра называют его полный механический момент, который является суммой собственных моментов импульсов составляющих его частиц и их орбитальных механических моментов, обусловленных внутриядерными движениями. Спин ядра зависит от его состояния. Поэтому обычно подразумевают спин ядра в основном состоянии. Спин ядра определяют по количеству линий сверхтонкой структуры при спектроскопических исследованиях. Кроме спина для ядер характерные магнитные моменты. Магнитные моменты ядер выражаются в ядерных магнетонах, которые вводятся аналогично магнетону Бора, Существует однозначная связь между спином и статистикой ядра. Ядра с пивцилим спином подлежат статистике Ферми - Дирака, а с целым - статистике Бозе - Эйнштейна.

2. Энергия связи ядра. Удельная энергия связи. Энергия, которую надо затратить, чтобы, преодолев ядерные силы, расщепить ядро на отдельные нуклоны, называется энергией связи атомного ядра. Как следует из закона сохранения энергии, если ядро образуется из отдельных нуклонов, то энергия связи ядра в момент его формирования выделяется в виде излучения. Из закона взаимосвязи массы и энергии следует, что Е св =Dm·c 2 , где Dm-дефект массы ядра.

Рассчитаем суммарную массу покоя нуклонов, входящих в ядро какого-либо элемента: (Z·m p +(A-Z)·m n). Сравним получившееся число с массой ядра M я. Оказалось, что для всех элементов таблицы Менделеева масса ядра меньше суммарной массы частиц, входящих в состав ядра. Разница этих значений и называется дефектом массы:

Dm=Z·m p +(A-Z)·m n -M я

Итак, формула, по которой можно вычислить энергию связи, имеет вид:

Е св =(Z·m p +(A-Z)·m n -M я )·c 2

Энергия связи, приходящаяся на один нуклон, называется удельной энергией связи : dЕ=DЕ/А

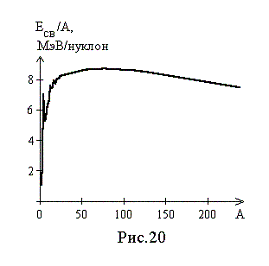
На рис. 20 представлен график зависимости удельной энергии связи от массового числа. Анализируя этот график, можно сделать следующие выводы:

1. Удельная энергия связи не является постоянной величиной для различных ядер, т.е. прочность связи нуклонов в различных ядрах различна. Наиболее прочно нуклоны связаны в ядрах с массовыми числами в диапазоне примерно от 40 до 100. Для этой группы ядер удельная энергия связи равна примерно 8,7 МэВ/нуклон.

2. Удельная энергия связи ядер с массовым числом А > 100 уменьшается и для урана составляет 7,6 МэВ.

3. В легких ядрах удельная энергия связи уменьшается с уменьшением числа нуклонов в ядре. Характерным для кривой удельной энергии связи в этой группе ядер является наличие острых максимумов и минимумов. Максимальное значение удельной энергии связи приходится на ядра а минимальное – на ядра

3. Формула Вайцзеккера для энергии связи.

Энергия связи:

Е св =c 2 . (1)

удобнее использовать следующую запись (с точностью до энергии связи электронов):

Рассмотрим отношение энергии связи ядра к массовому числу

По определению ε есть средняя энергия связи , приходящаяся на один нуклон (удельная энергия связи нуклона в ядре). Тем самым она характеризует интенсивность ядерных сил. Как видно из рис. 1, при малых значениях массовых чисел ε резко возрастает и достигает максимума при А ≈ 5060 (порядка 8,38,8 МэВ). Нуклиды с такими массовыми числами наиболее устойчивы. С дальнейшим ростом А средняя энергия связи уменьшается, однако в широком интервале массовых чисел значение удельной энергии связи почти постоянно (=8 МэВ). Из сказанного следует, что можно записать(3)

Нетрудно понять, что если бы каждый нуклон ядра взаимодействовал с (А– 1) другими нуклонами, то полная энергия этого взаимодействия была бы пропорциональна произведению А(А – 1) ≈ А. Отличие этого соотношения от (3) указывает на свойство насыщения ядерных сил: каждый нуклон в ядре взаимодействует не со всеми остальными, а только с ограниченным числом соседних нуклонов. Ядерные силы – это силы притяжения, и, как свидетельствует факт существования стабильных ядер, при некоторых условиях они больше сил кулоновского отталкивания (энергия кулоновского отталкивания двух соседних протонов в ядре на порядок меньше энергии притяжения).

Зависимость средней энергии связи ε, отнесенной к одному нуклону, от массового числа

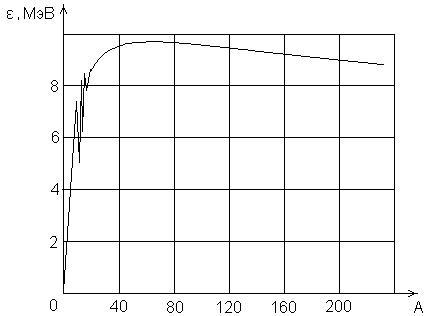Рис.1

Высвобождение энергии в реакциях синтеза или деления ядер обусловлено увеличением ε в процессе слияния самых легких ядер в более тяжелые или в процессах деления тяжелых ядер. Локальные максимумы кривой ε (А) связаны с образованием устойчивых ядерных оболочек.

Форма зависимости энергии связи от массового числа привела к мысли об аналогии между ядром и каплей жидкости, что привело к созданию капельной модели ядра и получению полуэмпирической формулы Вайцзеккера для энергии связи ядра.

,

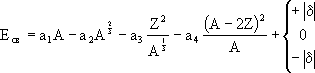где а 1 = 15,75 МэВ; а 2 = 17,8 МэВ; а 3 = 0,71 МэВ; а 4 = 23,7 МэВ; │δ│ = 34·А -3/4 . Первое слагаемое обуславливает пропорциональность энергии связи ядра и массы ядра равноценностью нуклонов ядра и взаимодействием каждого из них только с близлежащими соседями. Второе слагаемое учитывает то, что нуклоны на поверхности ядра взаимодействуют с меньшим числом других нуклонов и связаны с ними, таким образом, слабее (испарение молекул капли жидкости протекает с ее поверхности). Это приводит к уменьшению энергии связи ядра. Общее число «поверхностных» нуклонов пропорционально R 2 ~ А 2/3 . Третье слагаемое учитывает наличие сил кулоновского отталкивания между протонами (ΔЕ кул ~ Z(Z – 1)/R ≈ Z 2 /R ~ Z 2 /A 1/3). Четвертое слагаемое учитывает наличие протон-нейтронной асимметрии (наличие спина). Пятое слагаемое учитывает влияние четности Z и A – Z на устойчивость ядер: для четных-четных ядер (четное А и четное Z) подставляется в формулу +│δ│; для нечетно-нечетных ядер (четное А и нечетное Z) подставляется в формулу -│δ│; для нечетно-четных и четно-нечетных ядер (все остальные варианты) в формулу Вайцзеккера подставляется 0.

4. Формула Вайцзеккера для массы ядра.

Удельной энергией связи называют энергию связи, приходящуюся на один нуклон ядра. Ее определяют экспериментальным путем. Если разделить на полное число нуклонов в ядре А, то получится удельная энергия связи,

На рисунке 1 приведена зависимость экспериментальных значений от массового числа А. При рассмотрении этого рисунка можно сделать следующие выводы.

В самом деле, если бы каждый нуклон взаимодействовал со всеми остальными нуклонами ядра, то число таких парных взаимодействий было бы равно А(А-1)/2 и при Аи среднем значении энергии каждого парного взаимодействия ε полная энергия взаимодействия (в данном случае полная энергия связи ядра) была бы пропорциональна εи, стало быть, ВεА, т.е. возрастала бы линейно с ростом массового числа. Поскольку Вconst, приходиться допустить, что общее число связей пропорционально просто числу частиц А (а не ). Отсюда следует, что у каждого нуклона есть ограниченный запас возможностей взаимодействия, и если этот запас уже израсходован на связь с двумя – тремя соседними нуклонами, то наступает состояние насыщения и связи с другими нуклонами оказываются ослабленными даже на очень близких расстояниях.

Наиболее прочными являются ядра со средними массовыми числами (у них самые большие значения В).

В легких ядрах все или почти все нуклоны лежат на поверхности ядра и поэтому не в полной мере используют свои возможности взаимодействия, что несколько уменьшает значения В. С ростом А увеличивается доля нуклонов, лежащих внутри ядра, которые свои возможности взаимодействия используют полностью, поэтому значения В постепенно увеличиваются. Однако при дальнейшем увеличении числа нуклонов в ядре начинает все сильнее сказываться взаимное отталкивание электрических зарядов протонов, которое стремится разорвать ядро и поэтому уменьшает В. Это приводит к тому, что все тяжелые ядра оказываются нестабильными.

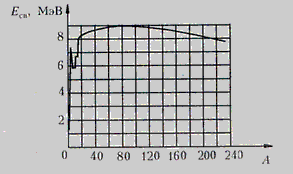
Рис.1

Расчет энергии связи ядра.

Энергия связи ядра численно равна работе, которую нужно затратить для расщепления ядра на отдельные нуклоны, или энергии, выделяющейся при синтезе ядер из нуклонов. Мерой энергии связи ядра является дефект массы.

Формула для расчета энергии связи ядра - это формула Эйнштейна: если есть какая-то система частиц, обладающая массой, то изменение энергии этой системы приводит к изменению ее массы.

Здесь энергия связи ядра выражена произведением дефекта масс на квадрат скорости света.

В ядерной физике массу частиц выражают в атомных единицах массы (а.е.м.).

Однако, в ядерной физике принято выражать энергию в электрон-вольтах (эВ):

Просчитаем соответствие 1 а.е.м. электрон-вольтам:

Теперь расчетная формула энергии связи (в электрон-вольтах) будет выглядеть так:

Перечислим основные характеристики ядер, которые будут обсуждаться далее:

1. Энергия связи и массы ядер.
2. Размеры ядер.
3. Спин ядра и моменты импульсов составляющих ядро нуклонов.
4. Четность ядра и частиц.
5. Изоспин ядра и нуклонов.
6. Спектры ядер. Характеристики основного и возбужденных состояний.
7. Электромагнитные свойства ядра и нуклонов.

1. Энергии связи и массы ядер

Масса стабильных ядер меньше суммы масс входящих в ядро нуклонов, разность этих величин и определяет энергию связи ядра:

(1.7)

Коэффициенты в (1.7) подбираются из условий наилучшего совпадения кривой модельного распределения с экспериментальными данными. Поскольку такая процедура может быть проведена по-разному, существует несколько наборов коэффициентов формулы Вайцзеккера. Часто используются в (1.7) следующие:

a 1 = 15.6 МэВ, a 2 = 17.2 МэВ, a 3 = 0.72 МэВ, a 4 = 23.6 МэВ,

Несложно оценить значение зарядового числа Z, при котором ядра становятся нестабильными по отношению к спонтанному распаду.
Спонтанный распад ядра возникает в случае, если кулоновское расталкивание протонов ядра начинает преобладать над стягивающими ядро ядерными силами. Оценка ядерных параметров, при которых наступает такая ситуация, может быть проведена из рассмотрения изменений в поверхностной и кулоновской энергиях при деформации ядра. Если деформация приводит к более выгодному энергетически состоянию, ядро будет спонтанно деформироваться вплоть до деления на два фрагмента. Количественно такая оценка может быть проведена следующим образом.
При деформации ядро, не меняя своего объема, превращается в эллипсоид с осями (см. рис. 1.2) .

Дефект массы. Согласно релятивистской механике масса покоя М устойчивой системы взаимосвязанных частиц меньше суммы масс покоя m 1 + m 2 +…+ m k тех же частиц, взятых в свободном состоянии. Разность

ΔМ = (m 1 + m 2 +…+ m k) – М называется дефектом массы системы частиц.

Уменьшение массы покоя свободных частиц при соединении их в устойчивую систему происходит вследствие освобождения некоторой части энергии покоя этих частиц. Выделившаяся энергия называется энергией связи.

Из закона сохранения энергии следует, что наименьшая энергия, которую нужно затратить, чтобы расчленить устойчивую систему взаимосвязанных частиц на отдельные свободные частицы, равна энергии связи.

Энергия связи прямо пропорциональна дефекту массы системы частиц ΔЕ = с 2 ΔМ , где с 2 – коэффициент перехода от массы к энергии, численно равный квадрату скорости света в вакууме; .

Если энергия выражена в мегаэлектрон - вольтах, а масса в атомных единицах, то с 2 = 931, 44 МэВ/а.е.м.

Дефект массы ΔМ атомного ядра есть разность между суммой масс свободных протонов и нейтронов и массой образовавшегося из них ядра ΔМ = (Ζm p + Nm n) – M , где Ζ – число протонов в ядре; N – число нейтронов (N = A – Ζ); m p и m n – массы свободных протона и нейтрона; М – масса ядра.

Ядерные реакции

Символическая запись ядерной реакции может быть дана или в развернутом виде, например

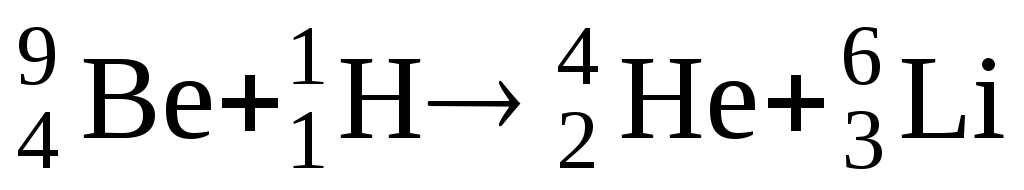, или сокращенно 9 Be(р, α) 6 Li.

Обозначения частиц: p – протон, n – нейтрон, d – дейтрон, t – тритон, α – альфа-частица, γ – гамма-фотон.

При решении задач применяются законы сохранения:

числа нуклонов А 1 + А 2 = А 3 + А 4 ;

заряда Ζ 1 + Ζ 2 = Ζ 3 + Ζ 4 ;

релятивистской полной энергии

Е 1 + Е 2 = Е 3 + Е 4 ;

импульса

.

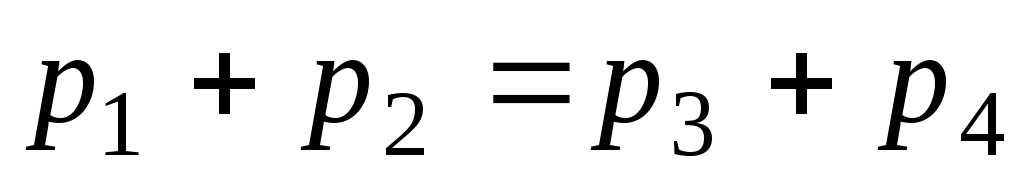Энергетический эффект ядерной реакции Q = c 2 [(m 1 + m 2) – (m 3 +m 4)],

где m 1 – масса покоя ядра – мишени; m 2 – масса покоя бомбардирующей частицы; m 3 + m 4 – сумма масс покоя ядер продуктов реакции.

Если m 1 + m 2 > m 3 +m 4 , то энергия освобождается, энергетический эффект положителен, реакция экзотермическая.

Если m 1 + m 2 < m 3 +m 4 , то энергия поглощается, энергетический эффект отрицателен, реакция эндотермическая.

4.1. Примеры решения задач

№ 1. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.

Р е ш е н и е.

Для определения энергии фотона воспользуемся сериальной формулой для водородоподобных ионов:

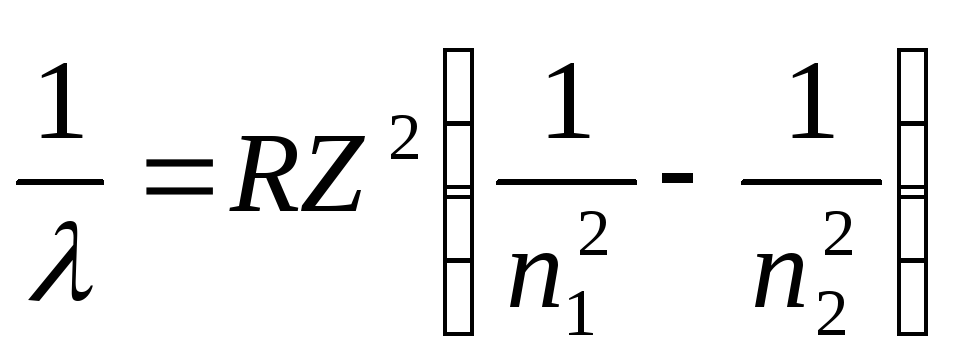, (1)

где  - длина волны фотона; R – постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n 1 – номер орбиты, на которую перешел электрон; n 2 – номер орбиты, с которой перешел электрон (n 1 и n 2 – главные квантовые числа).

Энергия фотона  выражается формулой  = hc / . Поэтому, умножив обе части равенства (1) на hc , получим выражение для энергии фотона

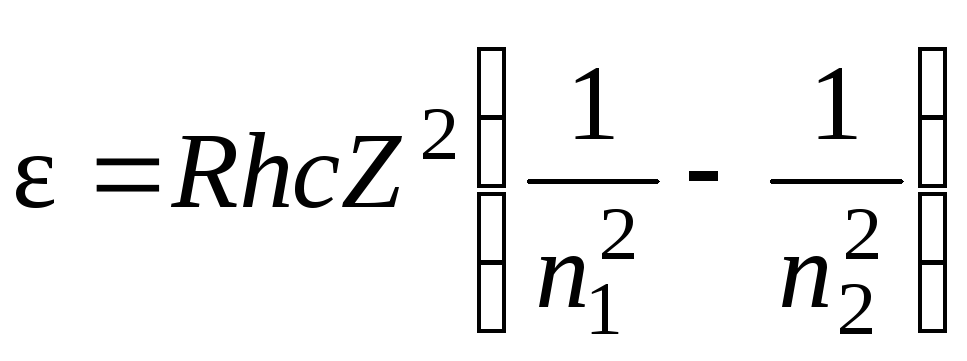. Так как величинаRhc- есть энергия ионизации E 1 атома водорода, то

.

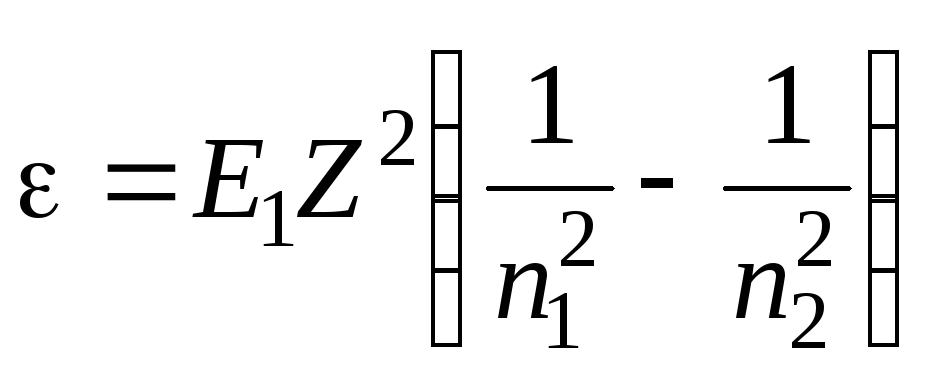Вычисления выполним во внесистемных единицах: Е 1 = 13,6 эВ; Z = 1 (заряд ядра атома водорода в относительных единицах, где за единицу заряда принято абсолютное значение заряда электрона); n 1 =2; n 2 = 4;

№ 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U . Найти длину волны де Бройля для двух случаев: 1) U 1 = 51 В; U 2 = 510 кВ.

Р е ш е н и е.

Длина волны де Бройля для частицы зависит от ее импульса р и определяется формулой:

 = h/р , (1)

где h – постоянная Планка.

Импульс частицы можно определить, если известна ее кинетическая энергия Т . Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).

Энергия связи E св ядра (A,Z) - выраженная в энергетических единицах разность между массой M(A,Z) ядра и суммой масс (A- Z) нейтронов и Zпротонов:

E св (A, Z) = [(A - Z)M n + ZM p ) - M(A,Z) ]c 2 .

Энергия связи ядра E св определяет минимальную энергию, которую надо затратить, чтобы разделить ядро на отдельные нуклоны.
Исходя из аналогии между заряженной жидкой каплей радиуса R= R 0 A 1/3 (где R 0 = 1.3 Фм ) и атомным ядром, К.Вайцзеккер в 1935 г. написал полуэмпирическую формулу для энергии связи ядра:

Значения коэффициентов a 1 - a 5 были подобраны так, чтобы наилучшим образом воспроизвести экспериментальные значения масс стабильных ядер:
a 1 = 15.6 МэВ, a 2 = 17.2 МэВ, a 3 = 0.72 МэВ, a 4 = 23.6 МэВ,

Энергия связи E св (A,Z) растет с ростом массового числа A, достигая величины
~ 2 ГэВ в области массовых чисел A~ 270. Поэтому гораздо более удобно использовать удельную энергию связи
ε = E св /A- энергию связи, приходящуюся на один нуклон (Рис. 2). Величина удельной энергии связи для большинства ядер ~ 8 МэB. Пропорциональность полной энергии связи числу нуклонов в ядре объясняется тем, что ядерные силы – короткодействующие, обладают свойством насыщения.
В рамках капельной модели ядра удалось объяснить многие свойства атомных ядер и получить полуэмпирическую формулу для энергии связи атомных ядер, которая позволила понять некоторые закономерности α- и β-распадов, процессов деления ядер и оценивать массы и энергии связи ядер.

Радиоактивностью называется способность атомного ядра самопроизвольно распадаться с испусканием частиц.
Радиоактивный распад ядра возможен тогда, когда он энергетически выгоден, т.е. сопровождается выделением энергии. Условием этого является превышение массы M исходного ядра суммы масс m i продуктов распада, которому соответствует неравенство M > ∑m i . Это условие является необходимым, но не всегда достаточным. Распад может быть запрещен другими законами сохранения – сохранения момента количества движения, электрического заряда, барионного заряда и т.д.
Радиоактивный распад характеризуется временем жизни радиоактивного изотопа, типом испускаемых частиц, их энергиями.
Основными видами радиоактивного распада являются:

• α-распад – испускание атомными ядрами α-частиц;
• β-распад – испускание атомными ядрами электрона и антинейтрино, позитрона и нейтрино, поглощение ядром атомного электрона с испусканием нейтрино;
• γ-распад – испускание атомными ядрами γ-квантов;
• спонтанное деление – распад атомного ядра на два осколка сравнимой массы.

К более редким видам радиоактивного распада относятся процессы испускания ядрами двух электронов, одного или двух протонов, а также кластеров – лёгких ядер от 12 C до 32 S. Во всех видах радиоактивности (кроме γ-распада) изменяется состав ядра – число протонов Z, массовое число Aили и то и другое одновременно.
На характеристики радиоактивного распада оказывает существенное влияние тип взаимодействия, вызывающего распад ядра. Так, α-распад вызывается сильным взаимодействием, β-распад - слабым, а γ-распад - электромагнитным.
Радиоактивный распад – статистический процесс. Каждое радиоактивное ядро может распасться в любой момент, и закономерности распада атомного ядра наблюдаются только в среднем, в случае распада достаточно большого количества ядер.
Для характеристики скорости (вероятности) радиоактивного распада используются три взаимосвязанные величины - постоянная распада λ, среднее время жизни tи период полураспада T 1/2 .
Постоянная распада λ - вероятность распада ядра в единицу времени. Если в образце в момент времени t имеется N радиоактивных ядер, то количество ядер dN, распавшихся за время dt, пропорционально N, λ и интервалу времени dt:

Закон радиоактивного распада имеет вид:

N(t)= N 0 e -λt ,

где N 0 – количество радиоактивных ядер в исходный момент времени t = 0.

Среднее время жизни τ:

.

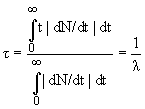Период полураспада T 1/2 – время, за которое первоначальное количество радиоактивных ядер уменьшается в два раза:

T 1/2 = ln2/λ=0.693/λ = τln2.

Размеры и форма ядра. Впервые размеры ядра правильно оценил Резерфорд, использовав для этой цели рассеяние альфа-частиц. Его первые эксперименты показали, что размеры заряженной части ядра – порядка 10 –14 м. Более поздние и более точные эксперименты позволили установить, что радиус ядра приблизительно пропорционален А 1/3 и, следовательно, плотность ядерного вещества почти постоянна. (Она колоссальна: 100 000 т/мм 3 .)

С открытием нейтрона стало ясно, что он представляет собой идеальное средство исследования ядра, поскольку нейтральные частицы, проходя на значительном удалении от ядра, не испытывают отклонения под действием заряда ядра. Другими словами, нейтрон сталкивается с ядром, если расстояние между их центрами оказывается меньше суммы их радиусов, а в противном случае не отклоняется. Опыты по рассеянию пучка нейтронов показали, что радиус ядра (в предположении сферической формы) равен:

R = r 0 A 1/3 ,

r 0 » 1,4×10 –15 м.

Таким образом, радиус ядра урана-238 равен 8,5×10 –15 м. Полученное значение соответствует радиусу действия ядерных сил; оно характеризует расстояние от центра ядра, на котором внешний нейтральный нуклон начинает впервые «ощущать» его воздействие. Такая величина радиуса ядра сравнима с расстоянием от центра ядер, на котором происходит рассеяние альфа-частиц и протонов.

Рассеяние альфа-частиц, протонов и нейтронов на ядрах обусловлено действием ядерных сил; следовательно, такие измерения радиусов ядер дают оценку радиуса действия ядерных сил. Взаимодействие же электронов с ядрами почти полностью определяется электрическими силами. Поэтому рассеяние электронов можно использовать для изучения формы распределения заряда в ядре. Эксперименты с электронами очень высоких энергий, проведенные Р.Хофстедтером в Станфордском университете, дали детальную информацию о распределении положительного заряда по радиусу ядра. На рис. 6 представлено угловое распределение рассеянных ядрами золота электронов с энергией 154 МэВ. Верхняя кривая характеризует угловое распределение, рассчитанное в предположении, что положительный заряд сконцентрирован в точке; очевидно, что экспериментальные данные этому предположению не соответствуют. Гораздо лучшее согласие достигается в предположении о равномерном распределении протонов по объему ядра (нижняя кривая). Однако «радиус заряда» оказывается примерно на 20% меньше радиуса «ядерных сил», полученного на основе данных по рассеянию нейтронов. Это может означать, что распределение протонов в ядре отличается от распределения нейтронов.