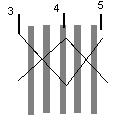
Чем состоит сущность интерференции света. В чем заключается явление интерференции света? Когда она наблюдается
Работа №8
ИЗУЧЕНИЕ ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА
Цель работы : Определить длину волны красного и зеленого света при помощи бипризмы Френеля.
Теория вопроса
Явление интерференции света состоит в том, что при сложении колебаний электромагнитных полей двух (или более) когерентных световых волн происходит перераспределение интенсивности в пространстве: в одних местах возникают максимумы в других минимумы. Наиболее отчетливо интерференция проявляется в том случае, когда колебания электронов
электромагнитных полей совершаются вдоль одного направления и амплитуды обеих интерферирующих волн одинаковы (). В этом случае в максимумах интенсивность I = 4I 1 , а в минимумах - I = 0. Интенсивность света пропорциональна квадрату амплитуды вектора напряженности электрического поля электромагнитной волны I=.Электромагнитная волна определяется колебаниями векторов
и электрического и магнитного полей. При формулировке условий интерференции выбирается вектор . Это связано с тем, что действие света на органы зрения, фотопластинки, фотоэлементы и другие приборы, предназначенные для его обнаружения, в основном определяется вектором электромагнитного поля.Две волны называются когерентными, если разность их фаз в определенной точке пространства постоянна во времени. Источники света называются когерентными, если они излучают когерентные световые волны. Естественные источники света некогерентны.
Когерентные световые волны можно получить, разделив (с помощью отражений и преломлений) волну, относящуюся к одному акту испускания источником, на две части (рис. 1), как бы испускаемые двумя когерентными источниками.
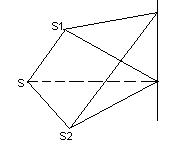
Пусть от двух когерентных источников до определенной точки Р в пространстве первая волна проходит в среде с показателем преломления n 1 путь l 1 , вторая волна проходит в среде с показателем преломления n 2 путь l 2 .
Если начальные фазы обеих волн равны нулю, колебания вектора
происходит вдоль одного направления и частоты колебаний одинаковы, первая волна возбудит в точке Р колебания напряженности электрического поляЕ=Е 1 +Е 2 =Е 01
+и будет совершать колебания с такой же частотой
, как напряженности Е 1 и Е 2 , и амплитудой равной . (2)Так как интенсивность I пропорциональна квадрату амплитуды, то
Величина
=L называется разностью оптических путей, проходимых волнами, или оптической разностью хода.Из (3) видно, что максимальная интенсивность в определенной точке пространства будет наблюдаться в том случае, если
()=1 (4) будет равна целому числу длин волн в вакууме: ; m=0,1,2… (5)Минимальная интенсивность в определенной точке пространства будет наблюдаться в том случае, если
()=-1 (6)или если оптическая разность хода
будет равна полуцелому числу длин волн в вакууме: ; m=0,1,2… (7)Условия (5) и (7) есть условия максимума и минимума соответственно.
Если два когерентных источника имеют вид узких параллельных щелей, то испускаемые ими цилиндрические волны при сложении будут давать интерференционную картину в виде чередующихся светлых и темных полос.
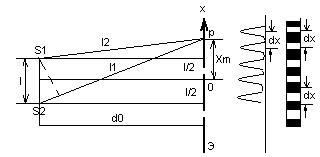
Пусть экран Э расположен параллельно плоскости, проходящей через источники S 1
и S 2
; источники находятся в воздухе (n 1
=n 2
=I); l – расстояние между когерентными источниками S 1
и S 2
; d 0
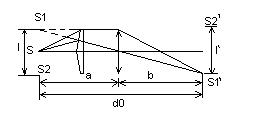
– расстояние от прямой, соединяющей источники, до экрана, на котором наблюдается интерференционная картина (l< Пользуясь схемой образования интерференционной картины (рис.2) и условием (5) можно найти расстояние между серединами двух ближайших максимумов (светлых полос) или мнимумов (темных полос) – ширину интерференционной полосы. В точке 0 экрана, лежащей на перпендикуляре к середине отрезка, соединяющего источники, наблюдается максимум, который называется центральным. В точке Р, находящейся на расстоянии x m
от центрального максимума, будет наблюдаться максимум с номером m, если оптическая разность хода волн окажется равной целому числу длин волн: Из рисунка 2 видно, что Из (9) и (10) следует, что Так как l< Тогда из (11) следует, что С учетом (8) Расстояние от центрального максимума до максимума номера m равно Расстояние между ближайшими максимумами или минимумами (ширина интерференционной полосы) равно В настоящей работе для получения интерференционной картины используется бипризма Френеля, представляющая двойную призму с малыми преломляющими углами Пучок света, падающий на бипризму (рис.3) от щели S, расположенной параллельно ребру тупого угла, вследствие преломления разделяются на два пучка когерентных цилиндрических волн, как бы исходящих из двух мнимых когерентных источников (изображений щели) S 1
и S 2
, колебания которых происходят синфазно (в одной фазе). Если тупой угол бипризмы близок к 180 0
, а угол падения на бипризму мал, то все лучи при преломлении отклонятся на одинаковый угол где n – показатель преломления стекла бипризмы. При этом мнимые источники S 1
и S 2
будут лежать практически в одной плоскости со щелью. Образовавшиеся пучки за бипризмой частично перекрываются, образуя зону интерференции. Интерференционная картина, наблюдаемая на экране, представляет чередование светлых и темных полос – максимумов и минимумов (рис. 2). Определив расстояние между когерентными источниками l, расстояние от источников до экрана d 0
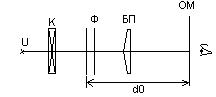
и ширину интерференционной полосы Описание установки
Схема установки (рис.4а) для определения ширины интерференционной полосы Ширина интерференционной полосы и расстояние между действительными изображениями щели l ’
измеряются при помощи окулярного микрометра. Расстояние между мнимыми источниками вычисляется по формуле увеличения тонкой линзы: где а – расстояние от линзы Л до мнимых источников (до щели), b - расстояние от линзы до действительных изображений (до окулярного микрометра). Расстояния d 0
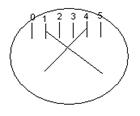
, а, b измеряются масштабной линейкой на оптической скамье по соответствующим указателям. Окулярный микрометр – приспособление, позволяющее измерять линейные размеры изображения, образованного какой – либо оптической системой в плоскости шкалы (в поле зрения окуляра). Окулярный микрометр состоит из кожуха, окуляра и барабана. В кожухе в фокальной плоскости окуляра находится неподвижная стеклянная пластинка со шкалой, имеющей восемь делений с ценой деления 1 мм. В этой же фокальной плоскости расположена также стеклянная пластинка с перекрестием и индексом, представляющим две тонкие параллельные черточки (рис. 5). Эта пластинка с помощью микрометрического винта связана с отсчетным барабаном так, что при вращении барабана перекрестие и индекс перемещаются в поле зрения окуляра относительно неподвижной шкалы. Шаг винта, перемещающего подвижную пластинку, равен 1мм. При повороте барабана на один оборот индекс и перекрестие перемещается в поле зрения окуляра на одно деление неподвижной шкалы. Барабан разделен на 100 делений, так что цена деления барабана винта составляет 0,01 мм. Полный отсчет окулярного микрометра складывается из отсчета по неподвижной шкале и барабану. Вопросы к зачету Литература Интерференция
— изменение в характере звуковых, тепловых, световых и электрических явлений, объясняемое колебательным движением: в первом случае частиц звучащего тела, в остальных трех — колебанием. Интерференция света
— частный случай интерференции для видимой области электромагнитного спектра; Волны — один из двух путей переноса энергии в пространстве (другой путь — корпускулярный, при помощи частиц). Волны обычно распространяются в какой-то среде (например, волны на поверхности озера распространяются в воде), однако направление движения самой среды не совпадает с направлением движения волн. Явление интерференции
происходит при взаимодействии двух и более волн одинаковой частоты, распространяющихся в различных направлениях. При этом оно наблюдается и у волн, распространяющихся в средах, и у электромагнитных волн. То есть интерференция является свойством волн как таковых и не зависит ни от свойств среды, ни от ее наличия. Самое поразительное происходит в точке встречи двух волн равной амплитуды, достигших места встречи в противофазе (то есть когда пик максимума амплитуды одной волны накладывается на пик минимума амплитуды другой). В таком случае, одна волна передает поверхности инструкцию «подняться на 1 м», а другая — «опуститься на 1 м», в результате чего поверхность воды просто остается на месте. В этом случае на воде мы наблюдаем точку штиля. В акустике — мертвую точку. В оптике — точку полного затемнения. Это явление называется интерференционным гашением волн, или деструктивной интерференцией. Возможна и прямо противоположная ситуация, когда две волны встречаются в точке совпадения фаз, и амплитуды колебаний среды складываются (при равной амплитуде встретившихся волн, например, амплитуда линейных колебаний среды удвоится). Это явление называется интерференционным усилением волн, или конструктивной интерференцией. Волны на поверхности воды в таких точках будут самыми высокими, звуки — самыми громкими, свет — самым ярким. Естественно, имеется множество промежуточных значений интерференционной амплитуды колебаний, лежащих в пределах от полностью конструктивной до полностью деструктивной интерференции, которые образуют причудливую и в то же время упорядоченную интерференционную картину взаимодействия волн. Эффект интерференционного гашения позволяет судить, имеем дело с волной или с частицей. Фактически, именно явление интерференции света окончательно убедило ученых XIX столетия в его волновой природе. Одним из простейших экспериментальных доказательств стал опыт британского ученого Томаса Юнга. Пучок света направлялся на непрозрачный экран-ширму с двумя параллельными прорезями, позади которого был установлен второй, проекционный экран. Если бы свет состоял из частиц, на проекционном экране были бы всего две параллельных полосы света, прошедших через прорези ширмы. А между ними проекционный экран оставался бы практически неосвещенным. Если же, с другой стороны, свет представляет собой распространяющиеся волны, картина должна наблюдаться принципиально иная. Согласно принципу Гюйгенса, каждая прорезь является источником вторичных волн. Эти волны, в частности, достигли бы линии в середине экрана, находящейся на равном удалении от прорезей синхронно и в одной фазе — гребень к гребню, провал к провалу. Значит, на серединной линии экрана оказалось бы выполненным условие максимального интерференционного усиления, и там должен наблюдаться максимум яркости. То есть наивысшая яркость окажется именно там, где она должна быть практически нулевой в случае справедливости корпускулярной гипотезы света. На каком-то удалении от центральной линии, напротив, волны должны оказаться в противофазе, и там будет наблюдаться темная полоса. По мере дальнейшего удаления от средней линии яркость будет снова возрастать до максимума, затем снова убывать и т. д. Таким образом, на проекционном экране мы должны получить целый ряд чередующихся интерференционных полос. И опыт Юнга это с блеском подтвердил, развеяв все сомнения в волновой природе света. Сюрприз ждал физиков столетием позже, когда через аналогичный экран с двумя щелями пустили пучок электронов. Выяснилось, что и они образуют на проекционном экране четкую интерференционную картину с чередованием «светлых» и «темных» полос. Следовательно, для электронов действительно выполняется соотношение де Бройля , хотя все привыкли считать их частицами! Интерференция сегодня широко применяется в экспериментальной физике, будучи положена в основу действия измерительного прибора под названием интерферометр. Интерферометры бывают самых разных конструкций, в зависимости от того, что именно они должны измерять, но принцип работы у любого интерферометра один и тот же: луч разбивается на два синфазных луча посредством использования частично пропускающего луч зеркала, после чего один луч направляется на экран напрямую, а другой — через исследуемый образец (конструкция прибора и частоты лучей могут быть самыми различными в зависимости от объекта исследований). В конечно итоге оба луча попадают на регистрационный экран, и по полученной интерференционной картине можно с большой точностью судить о свойствах исследуемого образца, поскольку смещение интерференционных полос позволяет отслеживать малейшие смещения фазы луча в результате взаимодействия с исследуемым веществом. Интерферометры позволяют регистрировать задержки светового луча на время значительно меньше полупериода световой волны. Именно опыт Майкельсона-Морли, проведенный с использованием точнейшего интерферометра и не выявивший эфирного ветра, заставил ученых окончательно отказаться от идеи мирового эфира. ИНТЕРФЕРЕНЦИЯ СВЕТА
- пространственное перераспределение энергии светового излучения при наложении двух или неск. световых волн, частный случай общего явления интерференции волн
. Нек-рые явления И. с. исследовались ещё И. Ньютоном в 17 в., но не могли быть им объяснены с точки зрения его корпускулярной теории. Правильное объяснение И. с. как типично волнового явления было дано в нач. 19 в. Т. Юнгом (Th. Young) и О. Френелем (A. Fresnel). Наиб, широко известна И. с., характеризующаяся образованием стационарной (постоянной во времени) интерференционной картины (и. к.) - регулярного чередования в пространстве областей повыш. и пониж. интенсивности света, получающейся в результате наложения когерентных световых пучков, т. е. в условиях постоянной (или регулярно меняющейся) разности фаз. Реже и только в спец. условиях эксперимента наблюдаются явления нестационарной И. с., к к-рым относятся световые биения и эффекты корреляции интенсивностей. Строгое объяснение явлений нестационарной И. с. требует учёта как волновых, так и корпускулярных свойств света и даётся на основе квантовой .
Стационарная И. с
. возникает при наличии когерентности
(определ. корреляции фаз) налагающихся волн. Взаимно световые пучки могут быть получены путём разделения и последующего сведения лучей, исходящих от общего источника света. При этом требование когерентности налагает нек-рые ограничения на угл. размеры источника и на ширину спектра излучения. Образование и. к. удобно проследить на идеализированной схеме классич. эксперимента Юнга (рис. 1). Точечный источник света S с
длиной волны l освещает два малых отверстия в экране А
, к-рые становятся вторичными взаимно когерентными источниками света (см. Дифракция света
).На экране В
наблюдается и. к., вызванная интерференцией
двух созданных систем волн. В соответствии с суперпозиции принципом
напряжённость эл--магн. поля E
Q в произвольной точке Q экрана В
даётся суммой напряжённостей полей E
1Q
и E 2Q , созданных в точке Q источниками 1 и 2. Наблюдаемой величиной является интенсивность излучения, падающего на экран, пропорциональная ср. квадрату напряжённости поля. Представляя напряжённость поля E i (t, s
)каждого источника (i=1,2) гармонич. ф-цией времени t и расстояния s
вдоль направления распространения Е
i (t,s)=E
i cos2p(vt+s/
l+j 0), где l, - длина волны, v
- частота, j 0 - нач. фаза световых , можно при надлежащем выборе единиц измерения напряжённости поля получить выражение для интенсивности I Q в точке Q в виде: Здесь I 1 = Интерференционные полосы наблюдаются в монохрома-тич. свете в любой плоскости области перекрытия расходящихся пучков от источников S 1 и S 2
(показано штриховкой). Из интерференц. устройств с делением волнового фронта большое практич. значение в спектроскопии имеет . решётка. Все схемы И. с. с делением волнового фронта предъявляют жёсткие требования к малости угл. размера источника света. Напр., в опыте Юнга при освещении отверстий 1 и 2 прямым солнечным светом, т. е. источником с угл. размером всего 0,5°, для получения чёткой и. к. расстояние между отверстиями не должно превышать неск. десятков микрон. Именно на резкой критичности контраста и. к. к размеру источника в схемах с делением волнового фронта основан метод измерения угл. размеров звёзд с помощью звёздного интерферометра (см. Интерферометр звёздный
).В схемах И. с. с амплитудным делением волнового поля излучение первичного источника делится полупрозрачными границами раздела оптич. сред. Так, напр., возникает широко распространённая в естеств. условиях И. с. в тонких плёнках, ответственная за радужное окрашивание масляных пятен на воде, мыльных пузырей, крыльев насекомых, окисных плёнок на металлах и др. Во всех этих случаях имеет место И. с., отражённого двумя поверхностями плёнок. В тонких плёнках перем. толщины при освещении протяжённым источником света картина интерференц. полос воспринимается локализованной на поверхности плёнки, причём данная интерференц. полоса соответствует фиксированной толщине плёнки (полосы равной толщины
.; рис. 3). Яркое интерференц. окрашивание возникает только для весьма тонких плёнок толщиной порядка длины волны, т. е. в низких порядках интерференции. Для более толстых плёнок и. к. видна при освещении монохроматизированным светом, напр, в свете натриевой лампы низкого давления. В тонких плёнках строго Интерференция
— взаимное усиление или ослабление двух или большего числа волн при их наложении друг на друга.
В результате интерференции
происходит перерас-пределение энергии светового излучения в пространстве. Устойчивая (стационарная, постоянная во времени) интер-ференционная картина наблюдается при сложении коге-рентных волн.
Латинское слово «
cohaerens» означает «находя-щийся в связи». И в пол-ном соответствии с этим значением под когерент-ностью понимают корре-лированное протекание во времени и простран-стве нескольких волно-вых процессов.
Требование когерентности волн
— ключе-вое при рассмотрении интерференции. Разберем его на примере сложения двух волн одинаковой частоты. Пусть в некоторой точке пространства они возбуждают одинаково направленные (E̅ 1
E̅ 2
) колебания: E̅ 1
sin(ω̅
t +
φ 1 -)
и E̅ 2
sin(ω̅
t +
φ 2 -).
Тогда величина амплитуды результирующе-го колебания E̅
sin(ω̅
t +
φ)
равна E = √(E 1 2 +
E 2 2 +
2
E 1
E 2
cosδ),
где δ =
φ 1 —
φ 2 .
Если разность фаз δ
постоянна во времени, то волны называются когерентными
. Для некогерентных волн δ
случайным образом изменяется во времени, поэтому среднее значение cosδ
равно нулю. Поскольку интенсив-ность волны пропорциональна квадрату амплитуды, то в случае сложения некогерентных волн
интенсивность результирующей волны I
просто равна сумме интенсивно-стей каждой из волн: I =
I 1
+
I 2 .
При сложении
же коге-рентных волн
интенсивность результирующего колебания I =
I 1 +
I 2 + 2√(I 1
I 2
cosδ
),
в зависимости от значения cosδ
, мо-жет принимать значения и большие, и меньшие, чем I 1 +
I 2 .
Так как значение δ
в общем случае зависит от точки наблю-дения, то и интенсивность результирующей волны будет различной в разных точках. Именно это имелось в виду, ко-гда выше говорилось о перераспределении энергии в про-странстве при интерференции волн. Излучение с высокой степенью когерентности получают с помощью лазеров
. Но если нет лазера, когерентные волны можно получить, разделив одну волну на несколько. Обыч-но используют два способа «деления» — деление волнового фронта и деление амплитуды. При делении волнового фронта интерферируют волновые пучки, первоначально распространявшиеся от одного источника в разных напра-влениях, которые затем с помощью оптических приборов сводят в одной области пространства (ее называют полем интерференции
). Для этого используют бизеркала
и би-призмы Френеля
, билинзы Бийе
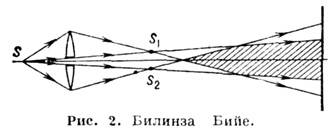
и др. Чтобы перечислить «цве-та» различных участков оптического диапазона в порядке убывания длины волны — красный, оран-жевый, желтый, зеленый, голубой, синий, фиолето-вый, достаточно вспом-нить фразу: «Каждый охотник желает знать, где сидит фазан».
При амплитудном де-лении волна разделяется на полупрозрачной границе двух сред. Затем, в результате последующих отражений и прело-млений, разделенные части волны встречаются и интерфе-рируют. Именно так окрашиваются в разные цвета мыль-ные пузыри и тонкие масляные пленки на воде, крылья стрекозы и оксидные пленки на металлах и оконных стек-лах. Важно, что интерферировать должны дуги волн, испу-щенные в одном акте излучения атома или молекулы, т. е. части волны должны «недолго» двигаться раздельно, иначе в точку встречи уже придут волны, испущенные раз-ными атомами. А так как атомы излучают спонтанно (если не созданы специальные условия, как в лазерах), то эти вол-ны будут заведомо некогерентны. В лазерах работает вынужденное излучение и этим достигается высокая степень когерентности. Материал с сайта
Явление интерференции
света
в XVII в. исследовал Ньютон. Он наблюдал ин-терференцию света в тон-ком воздушном зазоре между стеклянной плас-тинкой и положенной на нее линзой. Получающую-ся в таком опыте интерфе-ренционную картину так и называют — кольца Ньюто-на
. Однако Ньютон не смог внятно объяснить по-явление колец в рамках своей корпускулярной те-ории света. Лишь в начале XIX столетия сначала Т. Юнг, а затем О. Френель сумели объяснить образо-вание интерференцион-ных картин. И тот, и дру-гой были сторонниками волновой теории света.
Работа №8
ИЗУЧЕНИЕ ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА
Цель работы
: Определить длину волны красного и зеленого света при помощи бипризмы Френеля. Теория вопроса Явление интерференции света состоит в том, что при сложении колебаний электромагнитных полей двух (или более) когерентных световых волн происходит перераспределение интенсивности в пространстве: в одних местах возникают максимумы в других минимумы. Наиболее отчетливо интерференция проявляется в том случае, когда колебания электронов электромагнитных полей совершаются вдоль одного направления и амплитуды обеих интерферирующих волн одинаковы (). В этом случае в максимумах интенсивность I = 4I 1
, а в минимумах - I = 0. Интенсивность света пропорциональна квадрату амплитуды вектора напряженности электрического поля электромагнитной волны I=. Электромагнитная волна определяется колебаниями векторов и электрического и магнитного полей. При формулировке условий интерференции выбирается вектор . Это связано с тем, что действие света на органы зрения, фотопластинки, фотоэлементы и другие приборы, предназначенные для его обнаружения, в основном определяется вектором электромагнитного поля. Две волны называются когерентными, если разность их фаз в определенной точке пространства постоянна во времени. Источники света называются когерентными, если они излучают когерентные световые волны. Естественные источники света некогерентны. Когерентные световые волны можно получить, разделив (с помощью отражений и преломлений) волну, относящуюся к одному акту испускания источником, на две части (рис. 1), как бы испускаемые двумя когерентными источниками. Пусть от двух когерентных источников до определенной точки Р в пространстве первая волна проходит в среде с показателем преломления n 1
путь l 1
, вторая волна проходит в среде с показателем преломления n 2
путь l 2
. Если начальные фазы обеих волн равны нулю, колебания вектора происходит вдоль одного направления и частоты колебаний одинаковы, первая волна возбудит в точке Р колебания напряженности электрического поля Е=Е 1
+Е 2
=Е 01
+ и будет совершать колебания с такой же частотой , как напряженности Е 1
и Е 2
, и амплитудой равной Так как интенсивность I пропорциональна квадрату амплитуды, то I где Величина =L называется разностью оптических путей, проходимых волнами, или оптической разностью хода. Из (3) видно, что максимальная интенсивность в определенной точке пространства будет наблюдаться в том случае, если
()=1 (4) или если оптическая разность хода будет равна целому числу длин волн в вакууме: ; m=0,1,2… (5) Минимальная интенсивность в определенной точке пространства будет наблюдаться в том случае, если
()=-1 (6) или если оптическая разность хода будет равна полуцелому числу длин волн в вакууме: ; m=0,1,2… (7) Условия (5) и (7) есть условия максимума и минимума соответственно. Если два когерентных источника имеют вид узких параллельных щелей, то испускаемые ими цилиндрические волны при сложении будут давать интерференционную картину в виде чередующихся светлых и темных полос. Пусть экран Э расположен параллельно плоскости, проходящей через источники S 1
и S 2
; источники находятся в воздухе (n 1
=n 2
=I); l – расстояние между когерентными источниками S 1
и S 2
; d 0
– расстояние от прямой, соединяющей источники, до экрана, на котором наблюдается интерференционная картина (l< Пользуясь схемой образования интерференционной картины (рис.2) и условием (5) можно найти расстояние между серединами двух ближайших максимумов (светлых полос) или мнимумов (темных полос) – ширину интерференционной полосы. В точке 0 экрана, лежащей на перпендикуляре к середине отрезка, соединяющего источники, наблюдается максимум, который называется центральным. В точке Р, находящейся на расстоянии x m
от центрального максимума, будет наблюдаться максимум с номером m, если оптическая разность хода волн окажется равной целому числу длин волн: Из рисунка 2 видно, что Из (9) и (10) следует, что Так как l< Тогда из (11) следует, что С учетом (8) Расстояние от центрального максимума до максимума номера m равно Расстояние между ближайшими максимумами или минимумами (ширина интерференционной полосы) равно В настоящей работе для получения интерференционной картины используется бипризма Френеля, представляющая двойную призму с малыми преломляющими углами (30 ´). Пучок света, падающий на бипризму (рис.3) от щели S, расположенной параллельно ребру тупого угла, вследствие преломления разделяются на два пучка когерентных цилиндрических волн, как бы исходящих из двух мнимых когерентных источников (изображений щели) S 1
и S 2
, колебания которых происходят синфазно (в одной фазе). Если тупой угол бипризмы близок к 180 0
, а угол падения на бипризму мал, то все лучи при преломлении отклонятся на одинаковый угол : =(n-1), где n – показатель преломления стекла бипризмы. При этом мнимые источники S 1
и S 2
будут лежать практически в одной плоскости со щелью. Образовавшиеся пучки за бипризмой частично перекрываются, образуя зону интерференции. Интерференционная картина, наблюдаемая на экране, представляет чередование светлых и темных полос – максимумов и минимумов (рис. 2). Определив расстояние между когерентными источниками l, расстояние от источников до экрана d 0
и ширину интерференционной полосы , можно определить длину волны по формуле Описание установки
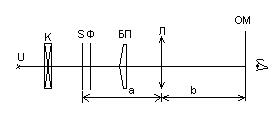
Схема установки (рис.4а) для определения ширины интерференционной полосы , расстояния d 0
состоит из осветителя И, К, раздвижной щели S, светофильтров Ф, бипризмы Френеля БП, окулярного микрометра ОМ, в фокальной плоскости которого наблюдается интерференционная картина. Для определения расстояния l между мнимыми изображениями щели дополнительно применяется собирающая линза Л (рис. 4б, в) с фокусным расстоянием 10-15 см. Все приборы располагаются на оптической скамье в держателях, снабженных указателями для отсчетов их положений. Приборы могут перемещаться в держателях вверх и вниз и закрепляться в требуемом положении. а) Ширина интерференционной полосы и расстояние между действительными изображениями щели l ’
измеряются при помощи окулярного микрометра. Расстояние между мнимыми источниками вычисляется по формуле увеличения тонкой линзы: где а – расстояние от линзы Л до мнимых источников (до щели), b - расстояние от линзы до действительных изображений (до окулярного микрометра). Расстояния d 0
, а, b измеряются масштабной линейкой на оптической скамье по соответствующим указателям. Окулярный микрометр – приспособление, позволяющее измерять линейные размеры изображения, образованного какой – либо оптической системой в плоскости шкалы (в поле зрения окуляра). Окулярный микрометр состоит из кожуха, окуляра и барабана. В кожухе в фокальной плоскости окуляра находится неподвижная стеклянная пластинка со шкалой, имеющей восемь делений с ценой деления 1 мм. В этой же фокальной плоскости расположена также стеклянная пластинка с перекрестием и индексом, представляющим две тонкие параллельные черточки (рис. 5). Эта пластинка с помощью микрометрического винта связана с отсчетным барабаном так, что при вращении барабана перекрестие и индекс перемещаются в поле зрения окуляра относительно неподвижной шкалы. Шаг винта, перемещающего подвижную пластинку, равен 1мм. При повороте барабана на один оборот индекс и перекрестие перемещается в поле зрения окуляра на одно деление неподвижной шкалы. Барабан разделен на 100 делений, так что цена деления барабана винта составляет 0,01 мм. Полный отсчет окулярного микрометра складывается из отсчета по неподвижной шкале и барабану. Для определения размера изображения перекрестие наводится последовательно на две точки изображения объекта, и производятся соответствующие отсчеты. Разность отсчетов дает искомый размер. Порядок выполнения работы Полученные данные занесите в таблицу формы I. Вопросы к зачету Литература![]() (9)
(9)
![]() (10)
(10)
![]() , (11)
, (11)
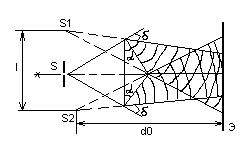

![]() , вторая – колебания
, вторая – колебания ![]() ., где , , с – скорость света в вакууме. Результирующая напряженность электрического поля в токе Р
равна
., где , , с – скорость света в вакууме. Результирующая напряженность электрического поля в токе Р
равна![]() (1)
(1)![]() ? (3)
? (3)![]() - разность фаз между колебаниями Е 1
и Е 2
в точке Р, - длина волны в вакууме.
- разность фаз между колебаниями Е 1
и Е 2
в точке Р, - длина волны в вакууме.
![]() (9)
(9)![]() (10)
(10)![]() , (11)
, (11)