Изменение потенциальной энергии заряда формула. Потенциальная энергия взаимодействия точечных зарядов
§ 12.3 Работа сил электростатического поля. Потенциал. Эквипотенциальные поверхности
На заряд q пр помещённый в произвольную точку электростатического поля с напряжённостью Е, действует сила F= q пр E. Если заряд не закреплён, то сила заставит его перемещаться и, значит, будет совершаться работа. Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда q пр из точки а электрического поля в точку b на отрезке пути dℓ, по определению, равна
(α - угол между F и направлением движения) (рис.12.13).
Если работа совершается внешними силами, то dA< 0 , если силами поля, то dA > 0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении q пр из точки a в точку b
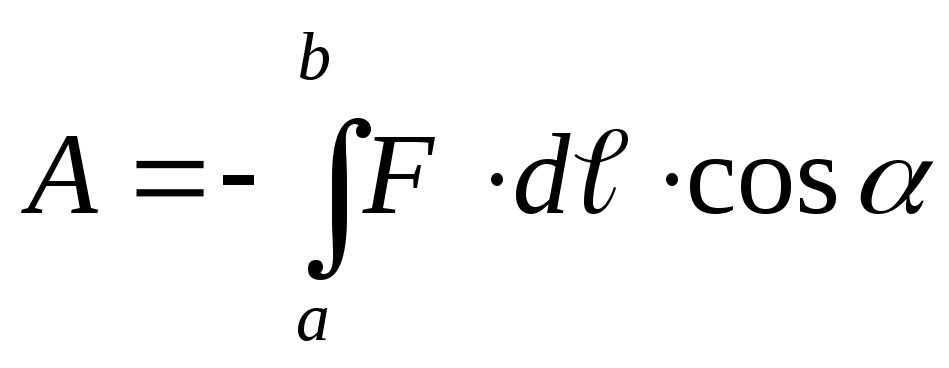 (12.20)
(12.20)
Рисунок -12.13
(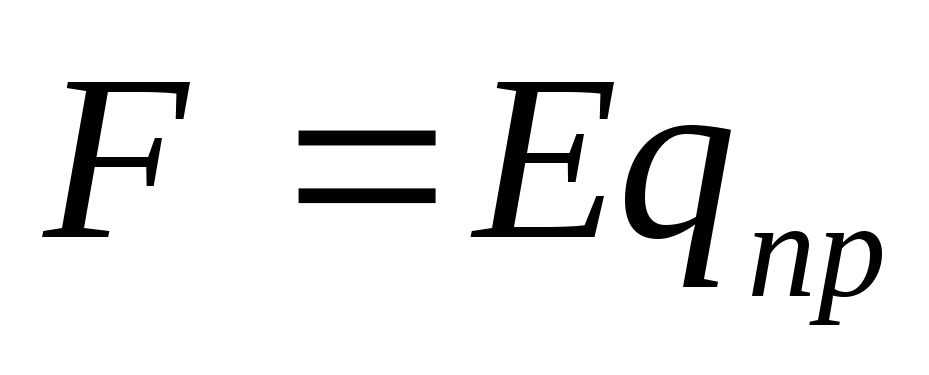 - кулоновская сила, действующая на
пробный зарядq пр
в каждой точке поля с напряжённостью
E).
- кулоновская сила, действующая на
пробный зарядq пр
в каждой точке поля с напряжённостью
E).
Тогда работа
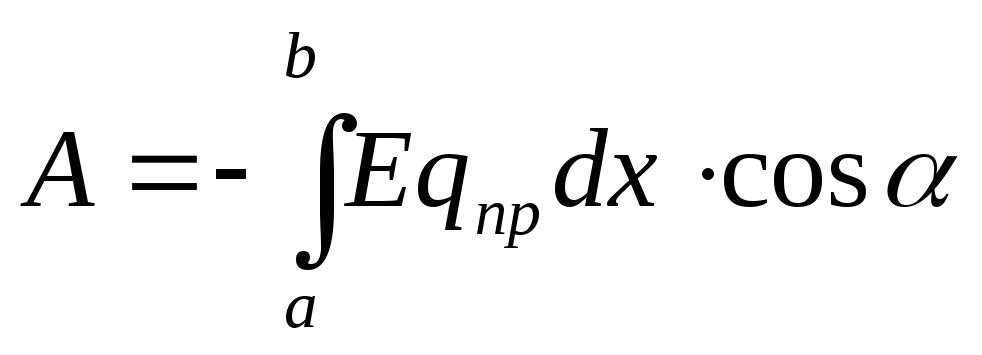 (12.21)
(12.21)
Перемещение
совершается перпендикулярно вектору
 ,
следовательноcosα
=1, работа переноса пробного заряда q пр
от a
к b
равна
,
следовательноcosα
=1, работа переноса пробного заряда q пр
от a
к b
равна
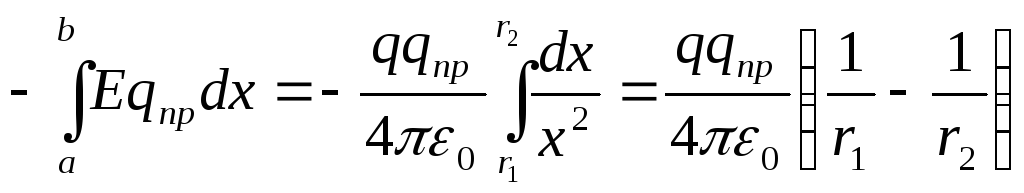 (12.22)
(12.22)
Работа сил электрического поля при перемещении заряда не зависит от формы пути, а зависит лишь от взаимного расположения начальной и конечной точек траектории.
Следовательно, электростатического поля точечного заряда является потенциальным , а электростатические силы – консервативными .
Это свойство потенциальных полей. Из него следует, что работа совершаемая в электрическом поле по замкнутому контуру, равна нулю:
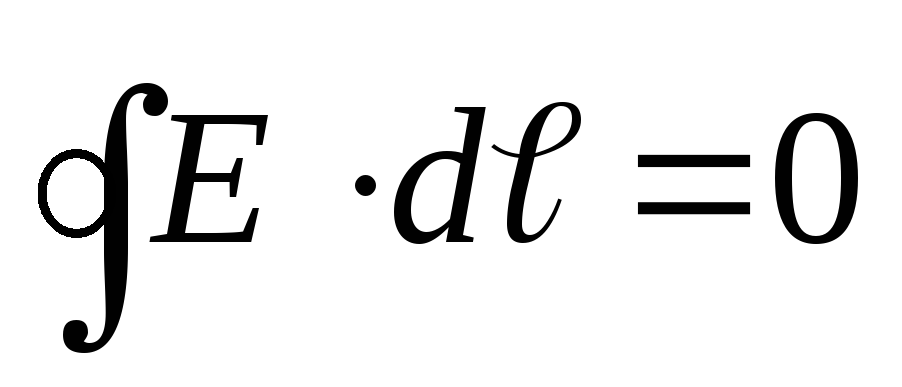 (12.23)
(12.23)
Интеграл
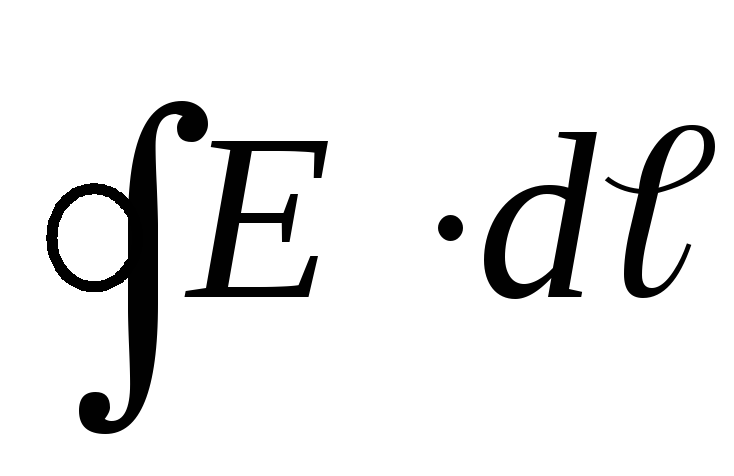 называется циркуляцией
вектора напряженности
.
Из обращения в нуль циркуляции вектора
Е следует, что линии напряжённости
электростатического поля не могут быть
замкнутыми, они начинаются на положительных
и кончаются на отрицательных зарядах.
называется циркуляцией
вектора напряженности
.
Из обращения в нуль циркуляции вектора
Е следует, что линии напряжённости
электростатического поля не могут быть
замкнутыми, они начинаются на положительных
и кончаются на отрицательных зарядах.
Как известно, работа консервативных сил совершается за счёт убыли потенциальной энергии. Поэтому, работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд q пр в начальной и конечной точках поля заряда q:
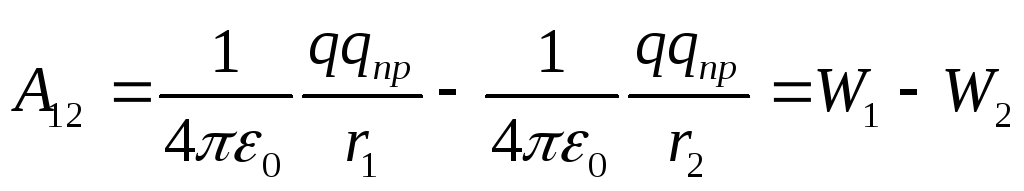 (12.24)
(12.24)
откуда следует, что потенциальная энергия заряда q пр в поле заряда q равна
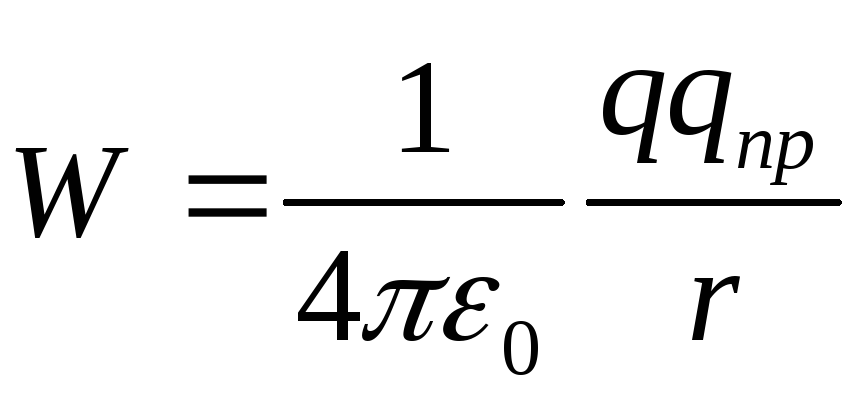 (12.25)
(12.25)
Для одноименных зарядов q пр q >0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноимённых зарядов q пр q < 0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.
Если поле создаётся системой n точечных зарядов q 1, q 2, …. q n , то потенциальная энергия U заряда q пр, находящегося в этом поле, равна сумме его потенциальных энергий U i , создаваемых каждым из зарядов в отдельности:
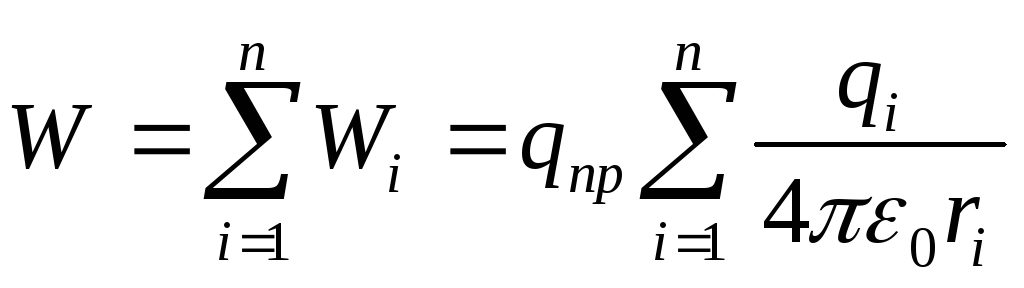 (12.26)
(12.26)
Отношение
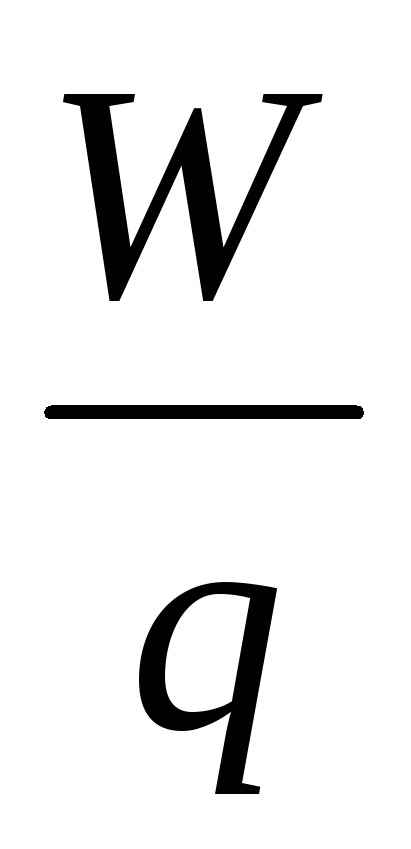 не зависят от зарядаq
и является энергетической характеристикой
электростатического поля.
не зависят от зарядаq
и является энергетической характеристикой
электростатического поля.
Скалярная физическая величина, измеряемая отношением потенциальной энергии пробного заряда в электростатическом поле к величине этого заряда, называется потенциалом электростатического поля.
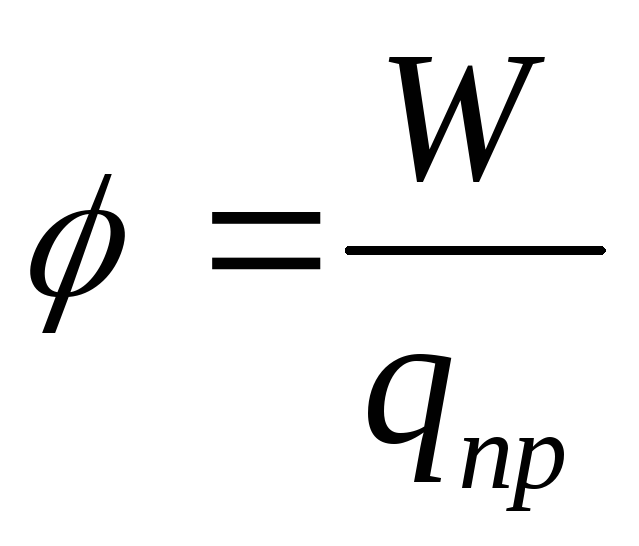 (12.27)
(12.27)
Потенциал поля, создаваемый точечным зарядом q, равен
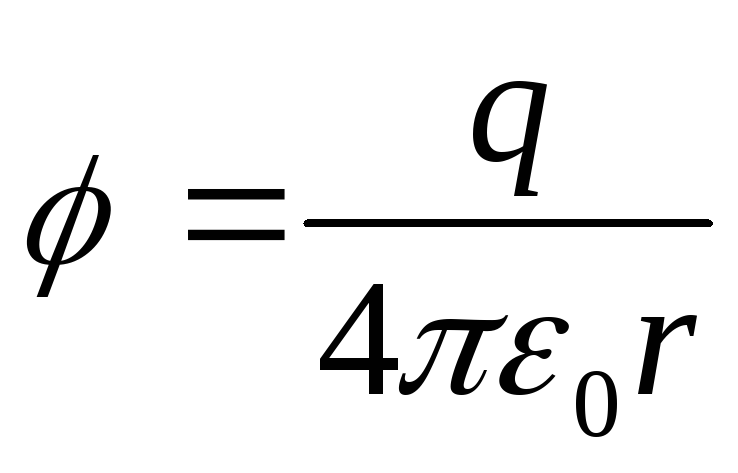 (12.28)
(12.28)
Единица потенциала – вольт .
Работа, совершаемая силами электростатического поля при перемещении заряда q пр из точки 1 в точку 2 может быть представлена как
т.е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.
Разность потенциалов двух точек электростатического поля φ 1 -φ 2 равна напряжению. Тогда
Отношение работы, совершаемой электростатическим полем при перемещении пробного заряда из одной точки поля в другую, к величине этого заряда называется напряжением между этими точками.
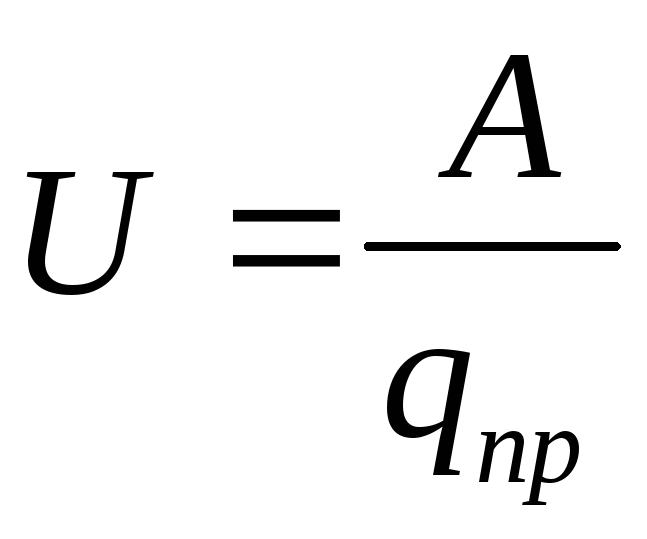 (12.30)
(12.30)
Графически электрическое поле можно изображать не только с помощью линий напряжённости, но и с помощью эквипотенциальных поверхностей.
Эквипотенциальные поверхности – совокупность точек, имеющих одинаковый потенциал. Из рисунка видно, что линии напряжённости (радиальные лучи) перпендикулярны эквипотенциальным линиям.
Э квипотенциальных
поверхностей вокруг каждого заряда и
каждой системы зарядов можно провести
бесчисленноемножество
(рис.12.14).
Однако их
проводят так, чтобы разности потенциалов
между любыми двумя соседними
эквипотенциальными поверхностями были
одинаковы. Тогда густота эквипотенциальных
поверхностей наглядно характеризует
напряжённость поля в разных точках.
Там, где эти поверхности расположены
гуще, напряжённость поля больше. Зная
расположение эквипотенциальных линий
(поверхностей), можно построить линии
напряжённости или по известному
расположению линий напряжённости можно
построить эквипотенциальные поверхности.
квипотенциальных
поверхностей вокруг каждого заряда и
каждой системы зарядов можно провести
бесчисленноемножество
(рис.12.14).
Однако их
проводят так, чтобы разности потенциалов
между любыми двумя соседними
эквипотенциальными поверхностями были
одинаковы. Тогда густота эквипотенциальных
поверхностей наглядно характеризует
напряжённость поля в разных точках.
Там, где эти поверхности расположены
гуще, напряжённость поля больше. Зная
расположение эквипотенциальных линий
(поверхностей), можно построить линии
напряжённости или по известному
расположению линий напряжённости можно
построить эквипотенциальные поверхности.
§ 12.4 Связь напряжённости и потенциала
Электростатическое поле имеет две характеристики: силовую (напряжённость) и энергетическую (потенциал). Напряжённость и потенциал – различные характеристики одной и той же точки поля, следовательно, между ними должна быть связь.
Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и х 1 – х 2 = dx , равна qЕ х dx. Та же работа равна q(φ 1 - φ 2)= -dφq. Приравнивая оба выражения, можем записать
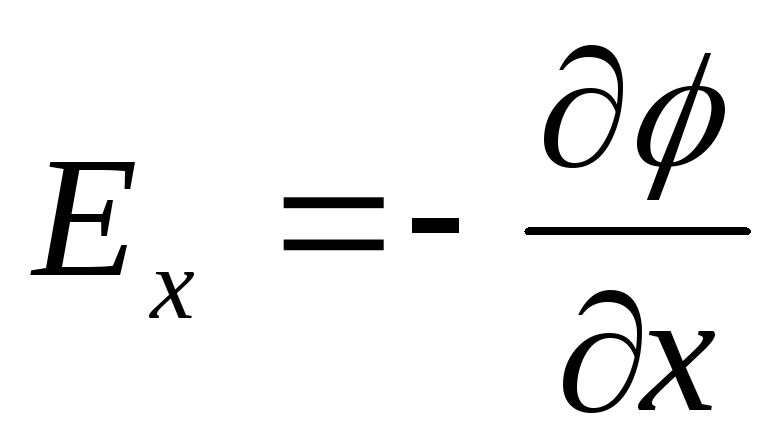
Повторив аналогичные
рассуждения для осей у и z,
можем найти вектор
 :
:
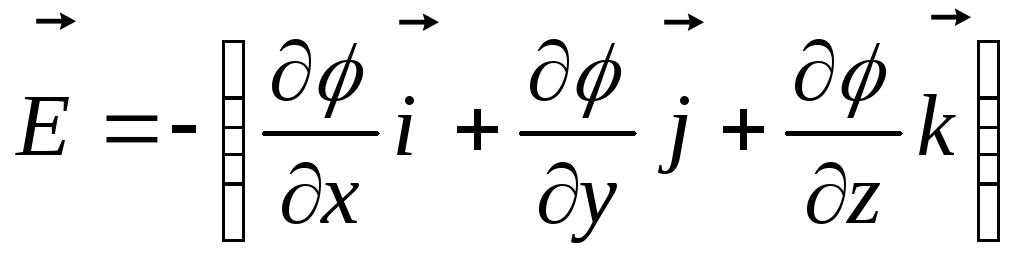
где
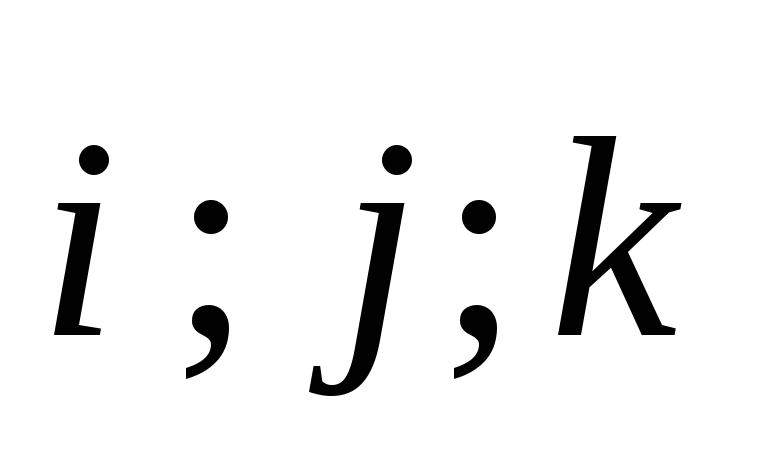 - единичные векторы координатных осей
х, у,z.
- единичные векторы координатных осей
х, у,z.
Из определения градиента следует, что
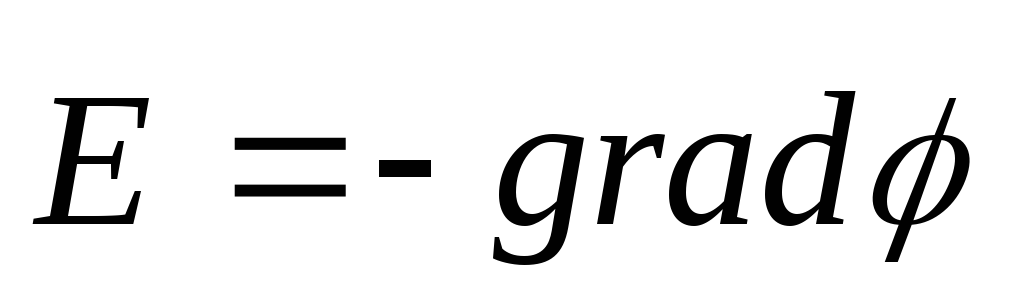 или
или
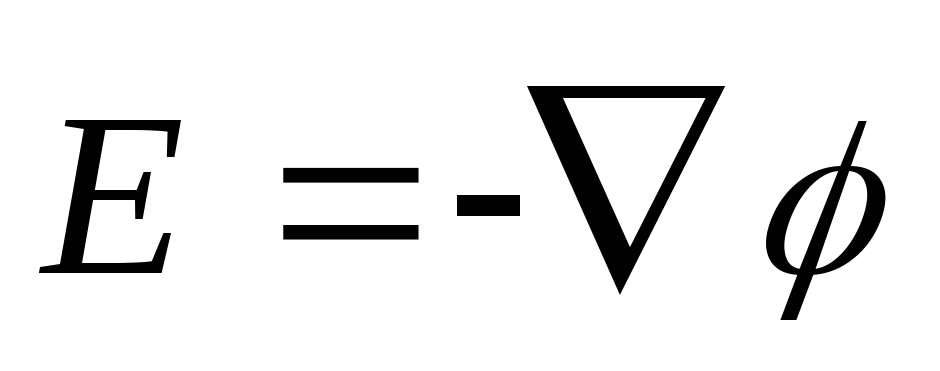 (12.31)
(12.31)
т.е. напряжённость поля Е равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости Е поля направлен в сторону убывания потенциала.
Установленная связь между напряжённостью и потенциалом позволяет по известной напряжённости поля найти разность потенциалов между двумя произвольными точками этого поля.
Поле равномерно заряженной сферы радиусом R
Напряжённость поля вне сферы определяется по формуле
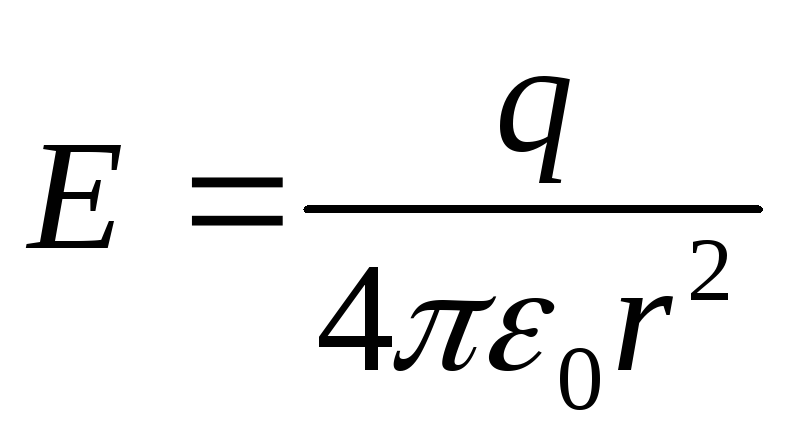 (r
>R)
(r
>R)
Разность потенциалов между точками r 1 и r 2 (r 1 >R; r 2 >R) определим, используя соотношение
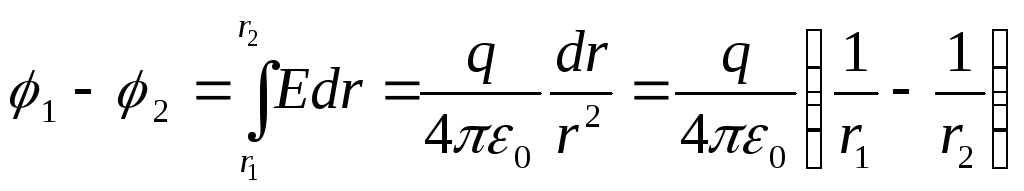

Потенциал сферы получим, если r 1 = R, r 2 → ∞:
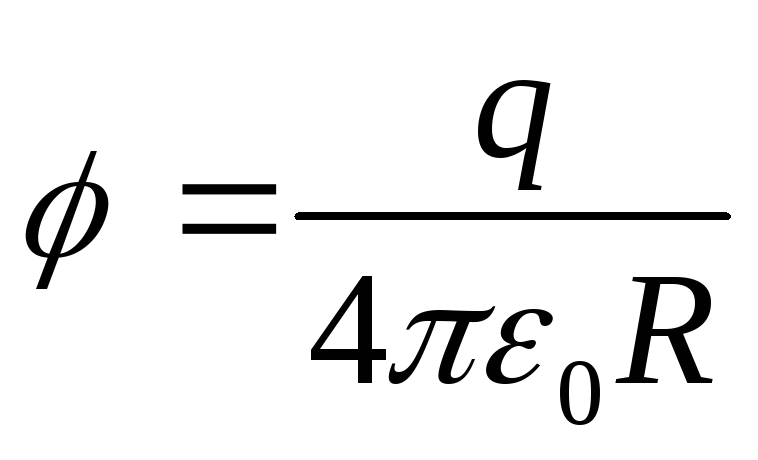
Поле равномерно заряженного бесконечно длинного цилиндра
Напряжённость поля вне цилиндра (r >R) определяется формулой
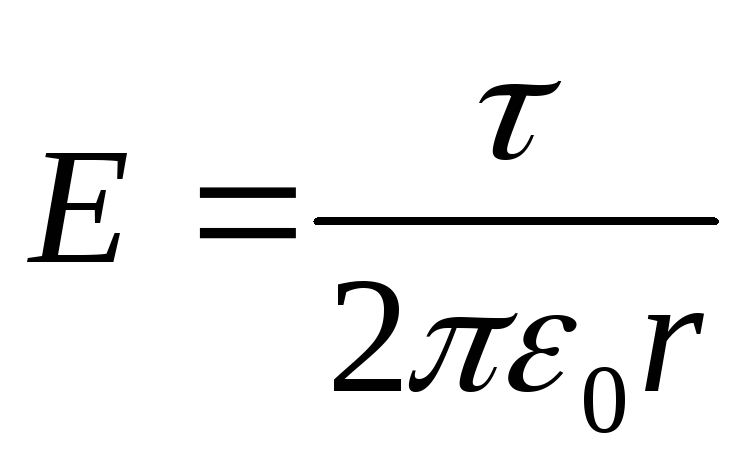
(τ – линейная плотность).
Разность потенциалов между двумя точками, лежащими на расстоянии r 1 и r 2 (r 1 >R; r 2 >R) от оси цилиндра, равна
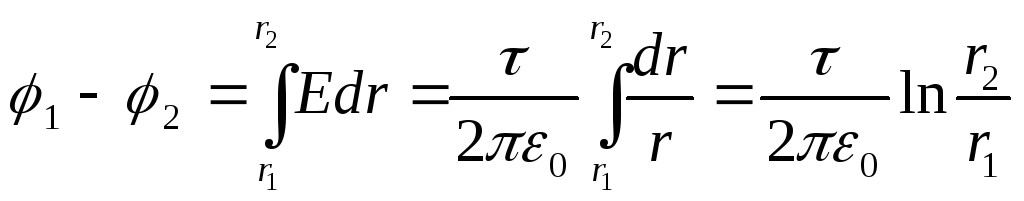 (12.32)
(12.32)
Поле равномерно заряженной бесконечной плоскости
Напряжённость поля этой плоскости определяется формулой
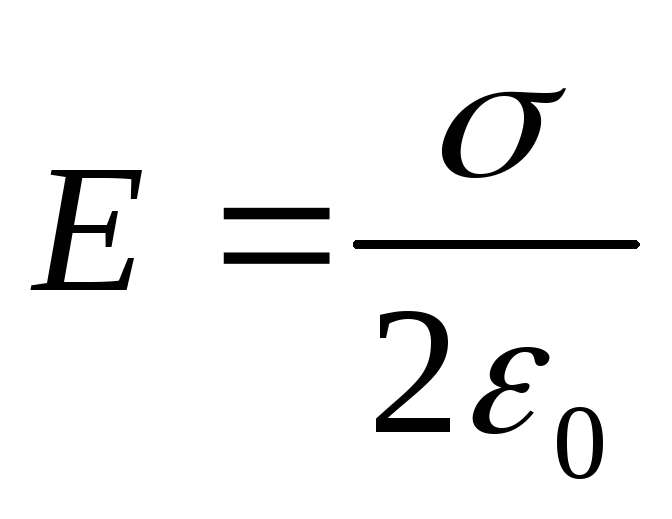
(σ - поверхностная плотность).
Разность потенциалов между точками, лежащими на расстоянии х 1 и х 2 от плоскости, равна
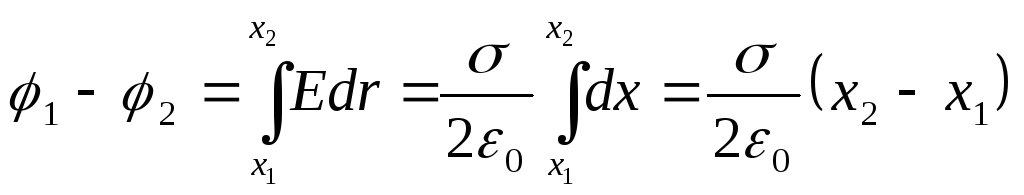 (12.33)
(12.33)
Поле двух разноименно заряженных бесконечных параллельных плоскостей
Напряженность поля этих плоскостей определяется формулой
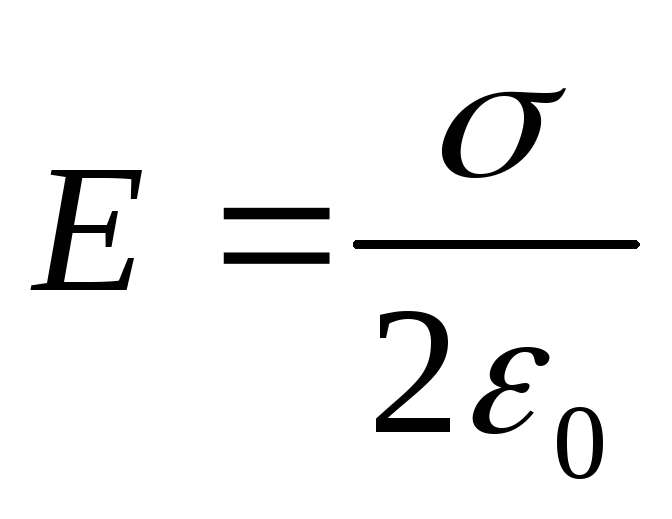
Разность потенциалов между плоскостями равна
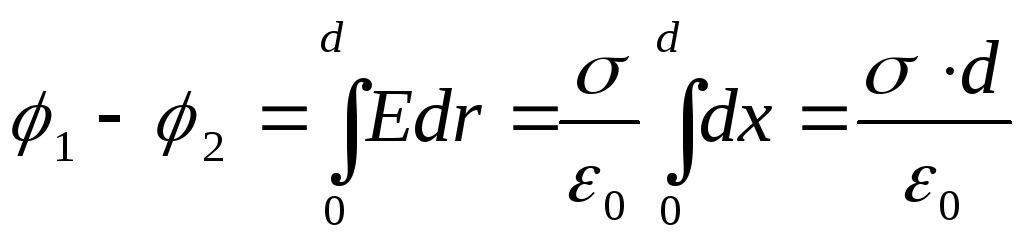 (12.34)
(12.34)
(d – расстояние между плоскостями).
Примеры решения задач
Пример 12.1 . Три точечных заряда Q 1 =2нКл, Q 2 =3нКл и Q 3 =-4нКл расположены в вершинах равностороннего треугольника со стороной длиной a =10см. Определите потенциальную энергию этой системы.
Дано : Q 1 =2нКл=2∙10 -9 Кл; Q 2 =3нКл=3∙10 -9 Кл; и Q 3 =-4нКл=4∙10 -9 Кл; a =10см=0,1м.
Найти : U .
Р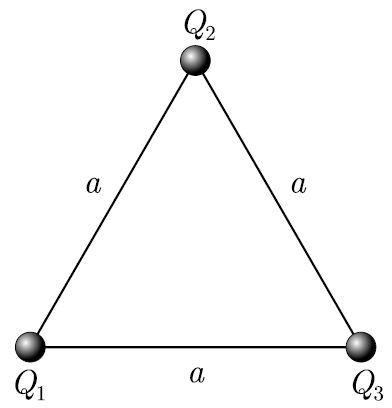 ешение:
Потенциальная
энергия системы зарядов равна
алгебраической сумме энергий взаимодействия
каждой из взаимодействующих пар зарядов,
т.е.
ешение:
Потенциальная
энергия системы зарядов равна
алгебраической сумме энергий взаимодействия
каждой из взаимодействующих пар зарядов,
т.е.
U=U 12 +U 13 +U 23
где соответственно потенциальные энергии одного из зарядов, находящегося в поле другого заряда на расстоянии а от него, равны
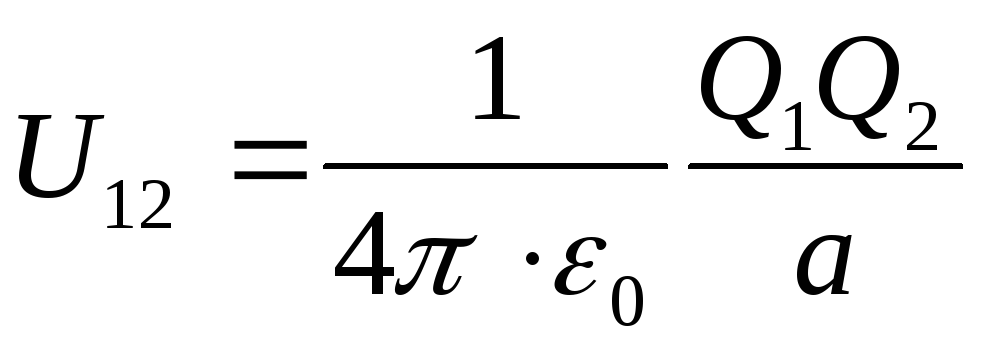 ;
;
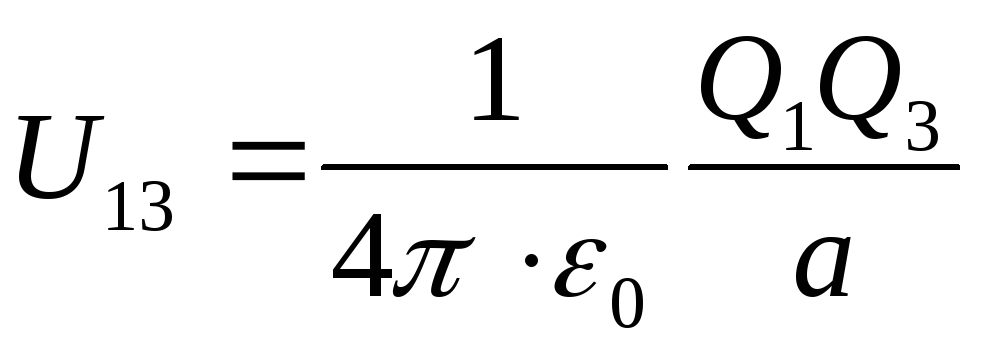 ;
;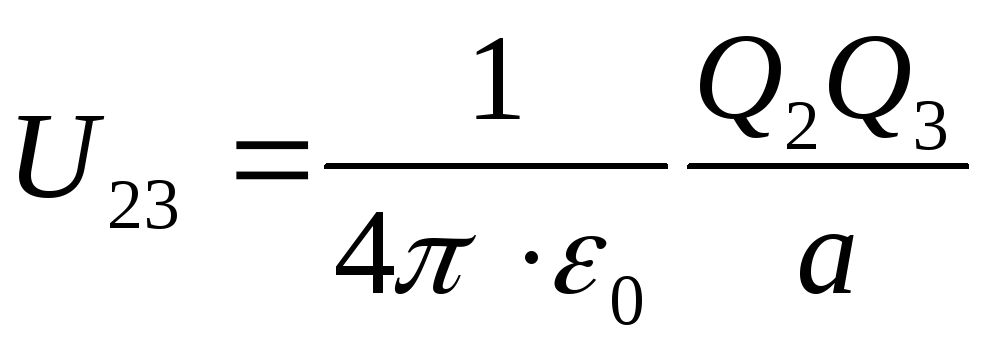 (2)
(2)
Подставим формулы (2) в выражение (1), найдём искомую потенциальную энергию системы зарядов
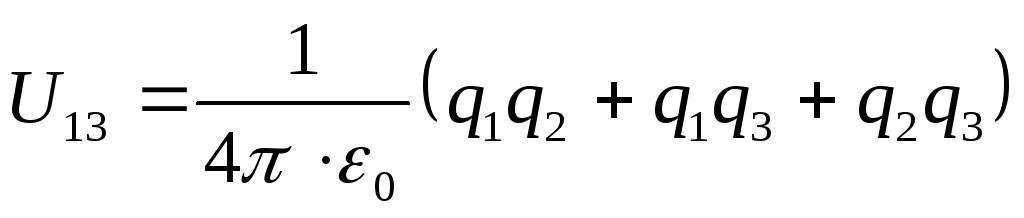
Ответ: U=-0,126мкДж.
Пример 12.2 . Определите потенциал в центре кольца с внутренним радиусом R 1 =30см и внешним R 2 =60см, если на нём равномерно распределён заряд q=5нКл.
Дано: R 1 =30см=0,3м; R 2 =60см=0,6м; q=5нКл=5∙10 -9 Кл
Найти : φ .
Решение: Кольцо разобьём на концентрические бесконечно тонкие кольца внутренним радиусом r и внешним – (r+dr).
Площадь рассматриваемого тонкого кольца (см.рисунок) dS=2πrdr.
П отенциал
в центре кольца, создаваемый бесконечно
тонким кольцом,
отенциал
в центре кольца, создаваемый бесконечно
тонким кольцом,
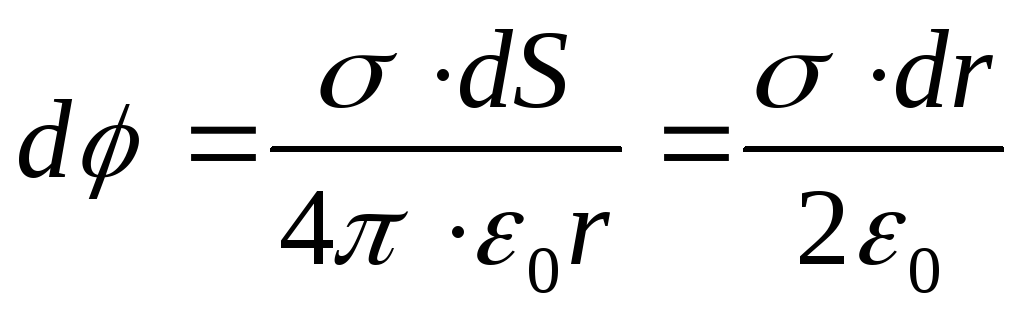
где – поверхностная плотность заряда.
Для определения потенциала в центре кольца следует арифметически сложить dφ от всех бесконечно тонких колец. Тогда
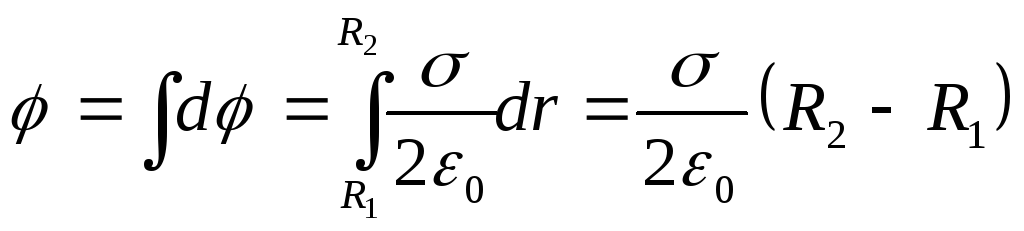
Учитывая, что заряд кольца Q=σS, где S= π(R 2 2 -R 1 2)- площадь кольца, получим искомый потенциал в центре кольца
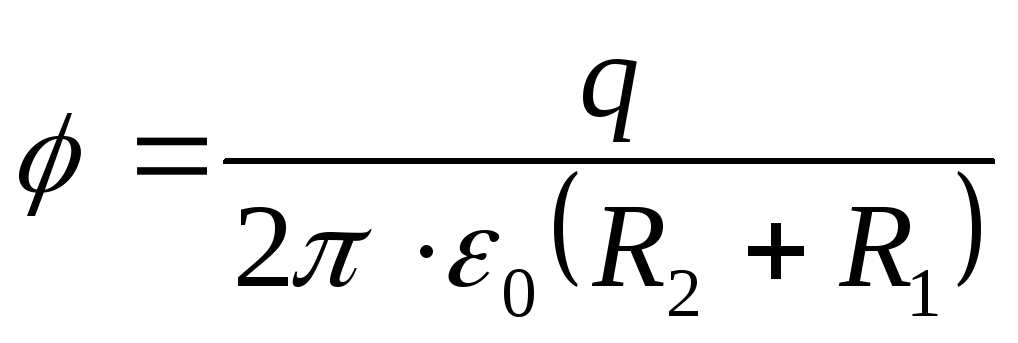
Ответ : φ=25В
Пример 12.3. Два точечных одноименных заряда (q 1 =2нКл и q 2 =5нКл) находятся в вакууме на расстоянии r 1 = 20см. Определите работу А, которую надо совершить, чтобы сблизить их до расстояния r 2 =5см.
Дано: q 1 =2нКл=2 ∙10 -9 Кл; q 2 =5нКл=5 ∙10 -9 Кл; r 1 = 20см=0,2м; r 2 =5см=0,05м.
Найти : А.
Решение: Работа, совершаемая силами электростатического поля при перемещении заряда Q из точки поля, имеющей потенциал φ 1 , в точку с потенциалом φ 2 .
A 12 = q(φ 1 - φ 2)
При сближении одноимённых зарядов работу совершают внешние силы, поэтому работа этих сил равна по модулю, но противоположна по знаку работе кулоновских сил:
A= -q(φ 1 - φ 2)= q(φ 2 - φ 1). (1)
Потенциалы точек 1 и 2 электростатического поля
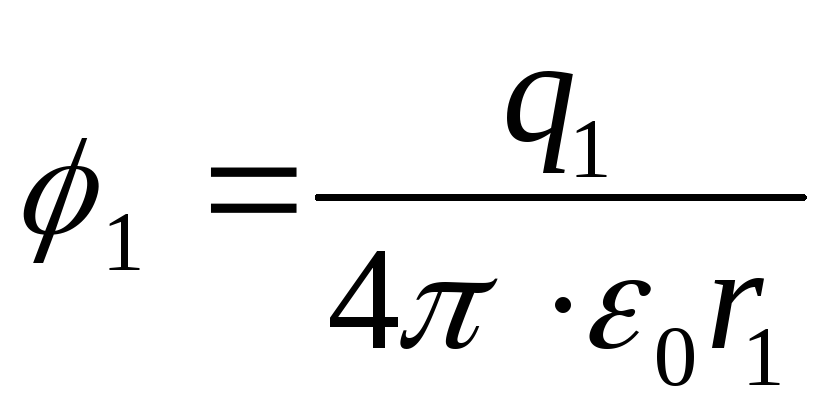 ;
;
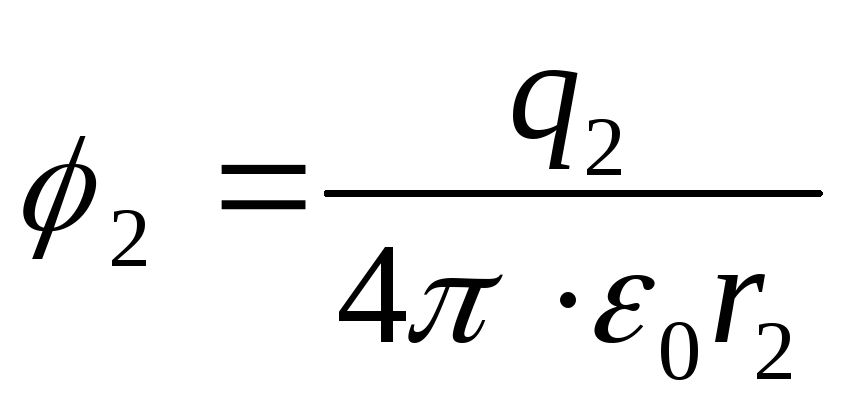 (2)
(2)
Подставив формулы (2) в выражение (1), найдём искомую работу, которую надо совершить, чтобы сблизить заряды,
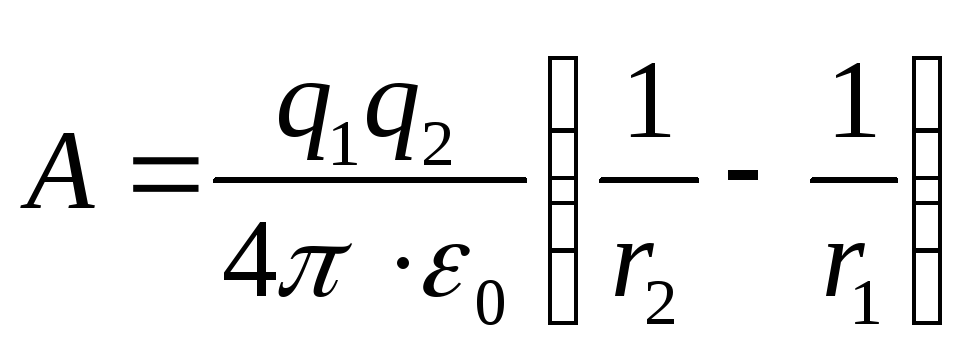
Ответ: А=1,35 мкДж.
Пример 12.4. Электростатическое поле создаётся положительно заряженной бесконечной нитью. Протон, двигаясь под действием электростатического поля вдоль линии напряжённости от нити с расстояния r 1 =2см до r 2 =10см, изменил свою скорость от υ 1 =1Мм/с до υ 2 =5Мм/с. Определите линейную плотность τ заряда нити..
Дано: q=1,6∙10 -19 Кл; m=1,67∙10 -27 кг; r 1 =2см=2∙10 -2 м; r 2 = 10см=0,1м; r 2 =5см=0,05м; υ 1 =1Мм/с=1∙10 6 м/с; до υ 2 =5Мм/с=5∙10 6 м/с.
Найти : τ .
Решение: Работа, совершаемая силами электростатического поля при перемещении протона из точки поля с потенциалом φ 1 в точку с потенциалом φ 2 идёт на увеличение кинетической энергии протона
q(φ 1 - φ 2)=ΔТ (1)
В случае нити электростатическое поле обладает осевой симметрией, поэтому
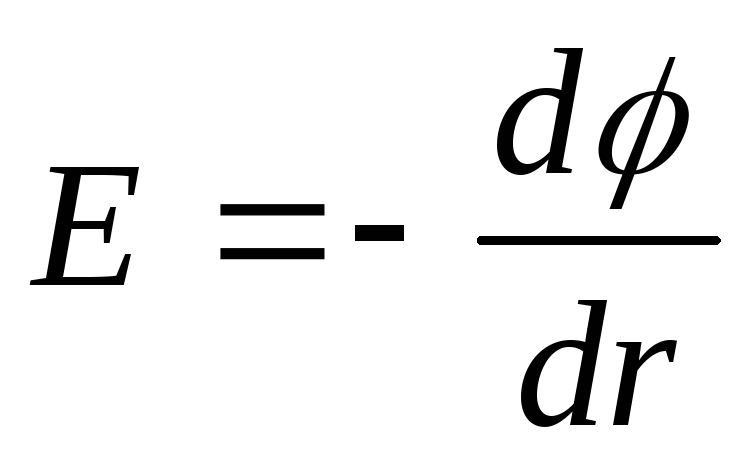 или dφ=-Edr,
или dφ=-Edr,
тогда разность потенциалов между двумя точками, находящимися на расстоянии r 1 и r 2 от нити,
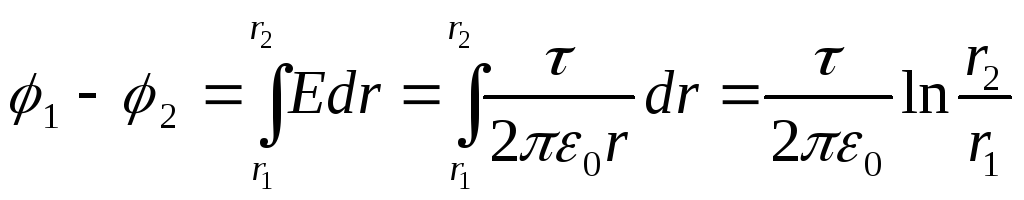
(учли, что
напряжённость поля, создаваемого
равномерно заряженной бесконечной
нитью,
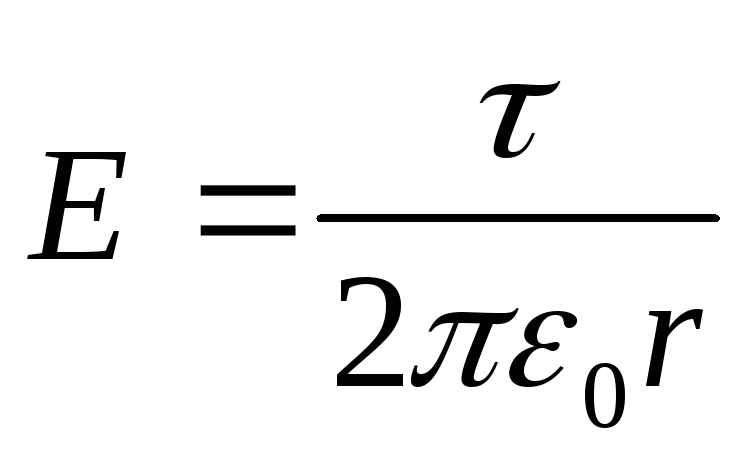 ).
).
Подставив выражение
(2) в формулу (1) и учитывая, что
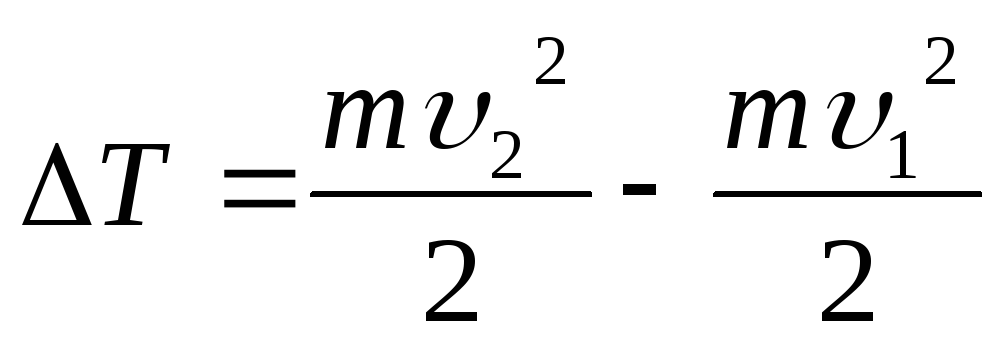 ,
получим
,
получим
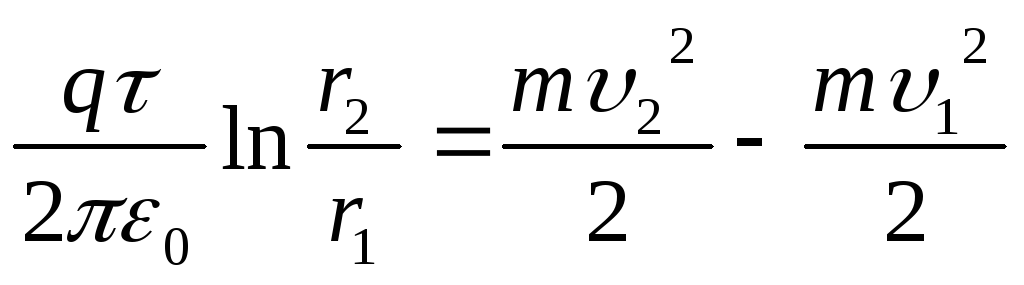
Откуда искомая линейная плотность заряда нити
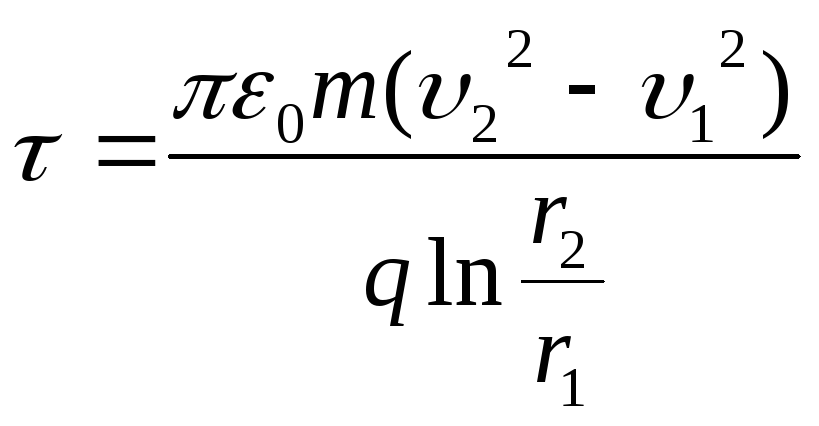
Ответ : τ = 4,33 мкКл/м.
Пример 12.5. Электростатическое поле создаётся в вакууме шаром радиусом R =8см, равномерно заряженными с объёмной плотностью ρ=10нКл/м 3 . Определите разность потенциалов между двумя точками этого поля, лежащими от центра шара на расстояниях: 1) r 1 =10см и r 2 =15см; 2) r 3 = 2см и r 4 =5см..
Дано: R=8см=8∙10 -2 м; ρ=10нКл/м 3 =10∙10 -9 нКл/м 3 ; r 1 =10см=10∙10 -2 м;
r 2 =15см=15∙10 -2 м; r 3 = 2см=2∙10 -2 м; r 4 =5см=5∙10 -2 м.
Найти : 1) φ 1 - φ 2 ; 2) φ 3 - φ 4 .
Решение: 1) Разность потенциалов между двумя точками, лежащими на расстоянии r 1 и r 2 от центра шара.
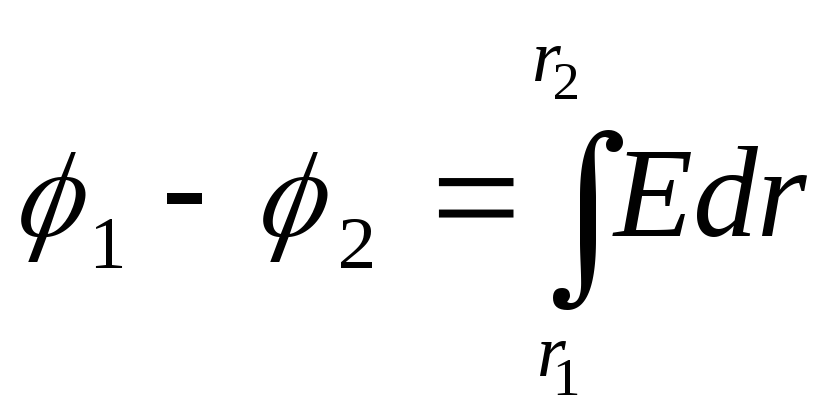 (1)
(1)
где
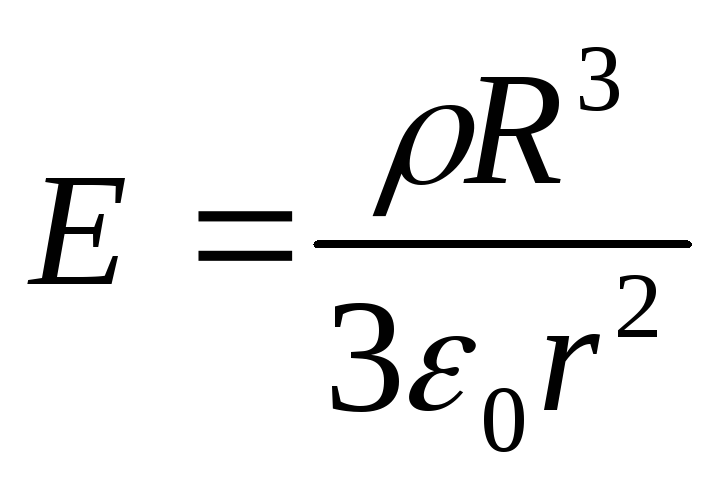 - напряжённость поля, создаваемого
равномерно заряженным с объёмной
плотностью ρ шаром, в любой точке, лежащей
вне шара на расстоянииr
от его центра.
- напряжённость поля, создаваемого
равномерно заряженным с объёмной
плотностью ρ шаром, в любой точке, лежащей
вне шара на расстоянииr
от его центра.
Подставив это выражение в формулу (1) и проинтегрировав, получим искомую разность потенциалов
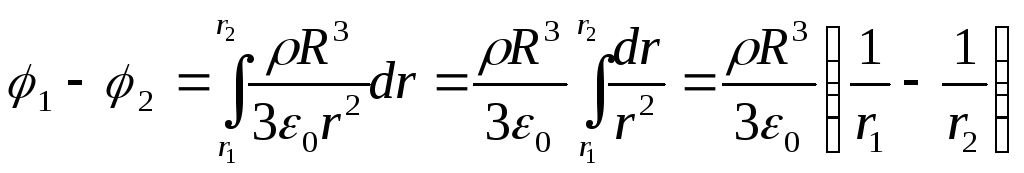
2) Разность потенциалов между двумя точками, лежащими на расстоянии r 3 и r 4 от центра шара,
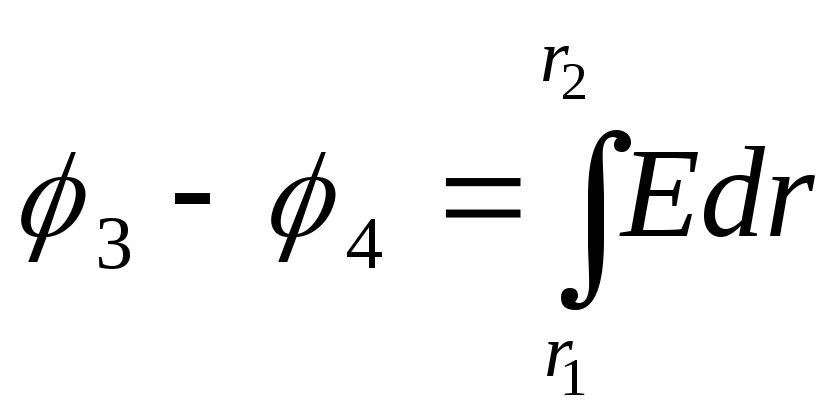 (2)
(2)
где
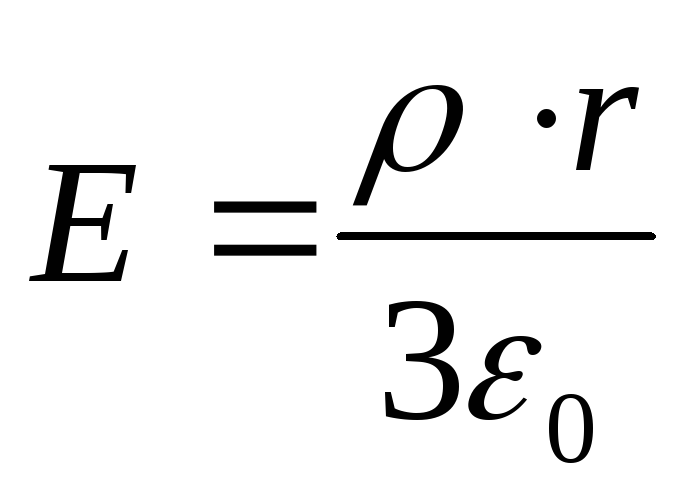 - напряжённость поля, создаваемого
равномерно заряженным с объёмной
плотностью ρ шаром, в любой точке, лежащей
внутри шара на расстоянииr
от его центра.
- напряжённость поля, создаваемого
равномерно заряженным с объёмной
плотностью ρ шаром, в любой точке, лежащей
внутри шара на расстоянииr
от его центра.
Подставив это выражение в формулу (2) и проинтегрировав, получим искомую разность потенциалов
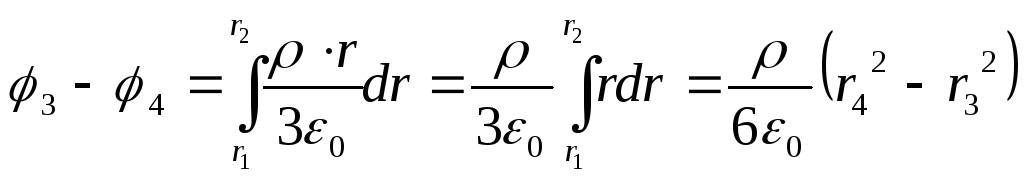
Ответ : 1) φ 1 - φ 2 =0,643 В; 2) φ 3 - φ 4 =0,395 В
Мы начнём с обсуждения потенциальной энергии, которую имеет заряд в электростатическом поле. Прежде всего необходимо вспомнить, при каких условиях можно вообще ввести понятие потенциальной энергии.
4.1 Консервативные силы
Сила называется консервативной (или потенциальной), если работа этой силы не зависит от формы траектории и определяется только начальным и конечным положением тела.
Пусть, например, тело под действием консервативной силы ~ переместилось из начальной
точки 1 в конечную точку 2 (рис. 16 ). Тогда работа силы~ зависит только от положения
самих точек 1 и 2, но не от траектории движения тела. Например, для траекторий 1 ! a ! 2 и 1 ! b ! 2 величина A будет одинаковой.
Рис. 16. К понятию консервативной силы
Отметим, что работа консервативной силы по любому замкнутому пути равна нулю. Действительно, давайте выйдем из точки 1 по траектории 1 ! a ! 2 и вернёмся назад по траектории 2 ! b ! 1. На первой траектории сила совершит работу A, а на второй траектории работа будет равна A. В итоге суммарная работа окажется нулевой.
Так вот, понятие потенциальной энергии можно ввести только в случае консервативной силы. Потенциальная энергия W это математическое выражение, зависящее от координат тела, такое, что работа силы равна изменению этого выражения со знаком минус:
Или, что то же самое:
A = (W2 W1 ) = W1 W2 :
Как видим, работа консервативной силы есть разность значений потенциальной энергии, вычисленных соответственно для начального и конечного положений тела.
Примеры консервативных сил вам хорошо известны. Например, сила тяжести является консервативной. Сила упругости пружины тоже консервативна. Именно поэтому мы можем говорить о потенциальной энергии тела, поднятого над землёй, или о потенциальной энергии деформированной пружины.
А вот сила трения не консервативна: работа силы трения зависит от формы траектории и не равна нулю на замкнутом пути. Поэтому не существует никакой ¾потенциальной энергии тела в поле силы трения¿.
![]()
4.2 Потенциальность электростатического поля
Оказывается, что сила, с которой электростатическое поле действует на заряженное тело, также является консервативной. Работа этой силы, совершаемая при перемещении заряда, называется работой электростатического поля. Имеем, таким образом, важнейший факт:
Работа электростатического поля не зависит от формы траектории, по которой перемещается заряд, и определяется лишь начальным и конечным положениями заряда. Работа поля по замкнутому пути равна нулю.
Этот факт называется также потенциальностью электростатического поля. Как и поле силы тяжести, электростатическое поле является потенциальным. Работа электростатического поля одинакова для всех путей, по которым заряд может двигаться из одной фиксированной точки пространства в другую.
Строгое математическое доказательство потенциальности электростатического поля выходит за рамки школьной программы. Однако ¾на физическом уровне строгости¿ мы можем убедиться в справедливости этого факта с помощью следующего простого рассуждения.
Нетрудно видеть, что если бы электростатическое поле не было потенциальным, то можно было бы построить вечный двигатель! В самом деле, тогда существовала бы замкнутая траектория, при перемещении заряда по которой поле совершало бы положительную работу (и при этом никаких изменений в окружающих телах не происходило бы). Крутим себе заряд по этой траектории, черпаем неограниченное количество энергии ниоткуда и все энергетические проблемы человечества решены:-) Но такого, увы, не наблюдается это вопиющим образом противоречит закону сохранения энергии.
Так как электростатическое поле потенциально, мы можем говорить о потенциальной энергии заряда в этом поле. Начнём с простого и важного случая.
4.3 Потенциальная энергия заряда в однородном поле
Потенциальная энергия тела, поднятого над землёй, равна mgh. Случай заряда в однородном поле оказывается очень похожим на эту механическую ситуацию.
Рассмотрим однородное электростатическое поле E, линии напряжённости которого направлены вдоль оси X (рис. 17 ). Пусть положительный заряд q перемещается вдоль силовой линии из точки 1 (с координатой x1 ) в точку 2 (с координатой x2 ).
0 x 1 | |||
Рис. 17. Перемещение заряда в однородном поле
Поле действует на заряд с силой ~ , которая направлена вдоль линий напряжённости. Работа
этой силы, как легко видеть, будет равна:
A = F (x2 x1 ) = qE(x2 x1 ):

Что изменится, если точки 1 и 2 не лежат на одной линии напряжённости? Оказывается, ничего! Формула для работы поля останется той же самой. Убедимся в этом с помощью рис. 18 .
0 x 1 | ||||
Рис. 18. Перемещение заряда в однородном поле
Двигаясь из точки 1 в точку 2, давайте выберем путь 1 ! 3 ! 2, где точка 3 лежит на одной силовой линии с точкой 1. Тогда работа A32 на участке 32 равна нулю ведь мы перемещаемся перпендикулярно силе. В результате получим:
A = A13 + A32 = A13 = qE(x2 x1 ):
Мы видим, что работа поля зависит лишь от абсцисс начального и конечного положений заряда. Запишем полученную формулу следующим образом:
A = qEx2 qEx1 = ((qEx2 ) (qEx1 )) = (W2 W1 ) = W:
Здесь W1 = qEx1 , W2 = qEx2 . Работа поля, в соответствии с формулой (8 ), оказывается равна изменению со знаком минус величины
Эта величина и есть потенциальная энергия заряда в однородном электростатическом поле. Через x обозначена абсцисса точки, в которой ищется потенциальная энергия. Нулевой уровень потенциальной энергии в данном случае соответствует началу координат x = 0 и на рисунках изображён пунктирной линией, перпендикулярной линиям напряжённости4 .
Напомним, что пока считается q > 0. Из формулы (9 ) следует, что при движении заряда вдоль силовой линии потенциальная энергия убывает с ростом x. Это естественно: ведь поле совершает положительную работу, разгоняя заряд, а кинетическая энергия заряда растёт за счёт убыли его потенциальной энергии.
Несложно показать, что формула (9 ) остаётся справедливой и для q < 0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.
Итак, важный вывод: в формуле для потенциальной энергии через q обозначается алгебраическая величина заряда (с учётом знака), а не его модуль.
4 На самом деле нулевой уровень потенциальной энергии можно выбирать где угодно. Иными словами, потенциальная энергия определена лишь с точностью до произвольной аддитивной постоянной C, т. е. W = qEx+C. Ничего страшного в такой неопределённости нет: физическим смыслом обладает на потенциальная энергия сама по себе, а разность потенциальных энергий, равная работе поля. В этой разности константа C сократится.
4.4 Потенциальная энергия взаимодействия точечных зарядов
Пусть два точечных заряда q1 и q2 находятся в вакууме на расстоянии r друг от друга. Можно показать, что потенциальная энергия их взаимодействия даётся формулой:
kq1 q2 | ||||
Мы принимаем формулу (10 ) без доказательства. Две особенности данной формулы следует обсудить.
Во-первых, где находится нулевой уровень потенциальной энергии? Ведь потенциальная энергия, как видно из формулы (10 ), в нуль обратиться не может. Но на самом деле нулевой уровень существует, и находится он на бесконечности. Иными словами, когда заряды расположены бесконечно далеко друг от друга, потенциальная энергия их взаимодействия полагается равной нулю (что логично в этом случае заряды уже ¾не взаимодействуют¿).
Во-вторых, q1 и q2 это снова алгебраические величины зарядов, т. е. заряды с учётом их знака.
Например, потенциальная энергия взаимодействия двух одноимённых зарядов будет положительной. Почему? Если мы отпустим их, они начнут разгоняться и удаляться друг от друга. Их кинетическая энергия возрастает, стало быть потенциальная энергия убывает. Но на бесконечности потенциальная энергия обращается в нуль, а раз она убывает к нулю, значит она является положительной.
А вот потенциальная энергия взаимодействия разноимённых зарядов оказывается отрицательной. Действительно, давайте удалим их на очень большое расстояние друг от друга так что потенциальная энергия равна нулю и отпустим. Заряды начнут разгоняться, сближаясь, и потенциальная энергия снова убывает. Но если она была нулём, то куда ей убывать? Только в сторону отрицательных значений.
Формула (10 ) помогает также вычислить потенциальную энергию системы зарядов, если число зарядов больше двух. Для этого нужно просуммировать энергии каждой пары зарядов. Мы не будем выписывать общую формулу; лучше проиллюстрируем сказанное простым примером, изображённым на рис.19 .
Рис. 19. Взаимодействие трёх зарядов
Если заряды q1 , q2 , q3 находятся в вершинах треугольника со сторонами a, b, c, то потенциальная энергия их взаимодействия равна:
kq1 q2 | kq2 q3 | kq1 q3 | |||||
4.5 Потенциал
Из формулы W = qEx мы видим, что потенциальная энергия заряда q в однородном поле прямо пропорциональна этому заряду.
То же самое мы видим из формулы W = kq1 q2 =r: потенциальная энергия заряда q1 , находящегося в поле точечного заряда q2 , прямо пропорциональна величине заряда q1 .
Работа
сил электрического поля, созданного
зарядом
,
по перемещению заряда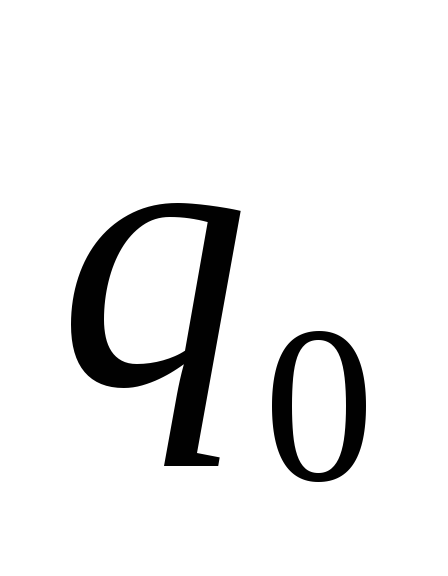 из точки 1 в точку 2 равна:
из точки 1 в точку 2 равна:
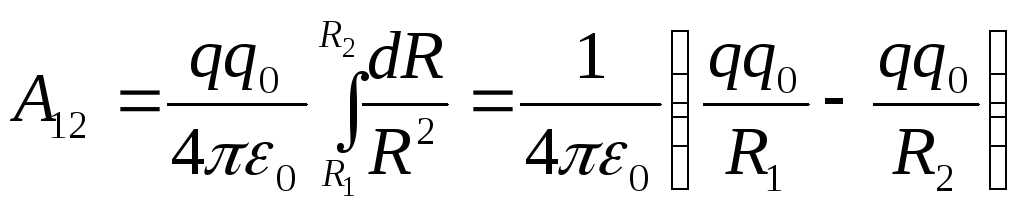 .
.
Работа сил консервативного поля равна убыли потенциальной энергии:
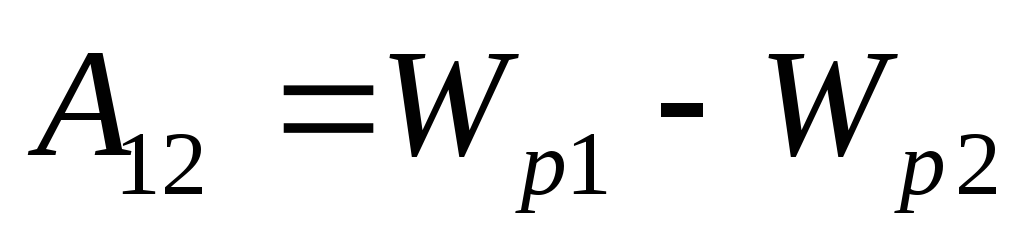 ,
,
тогда
потенциальная энергия заряда
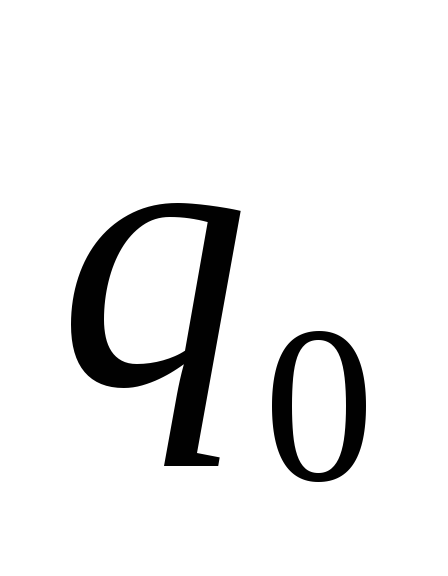 в поле заряда
в поле заряда равна:
равна:
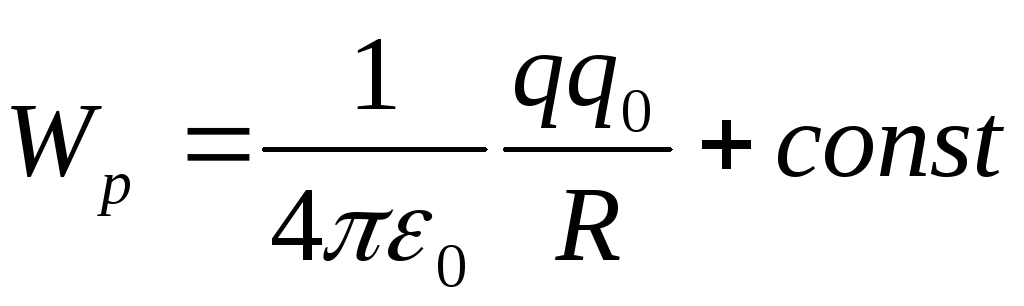 .
.
Значение
константы выбирается таким, чтобы при
удалении заряда на бесконечность (то
есть при
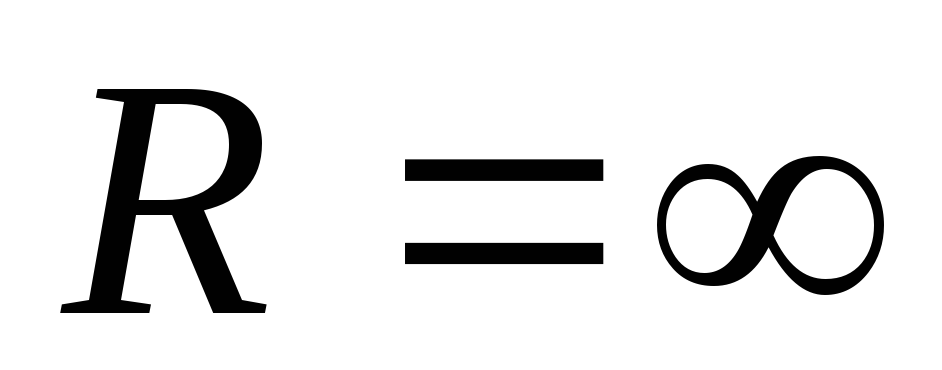 )
потенциальная энергия обратилась бы в
ноль, поэтому
)
потенциальная энергия обратилась бы в
ноль, поэтому
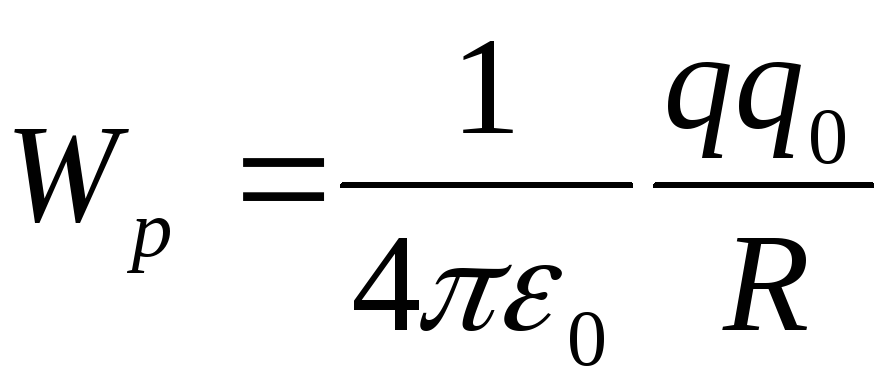 .
.
Ясно,
что разные пробные заряды
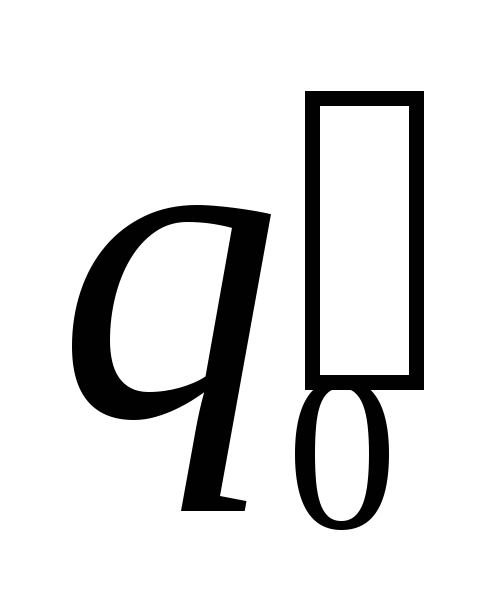 и
и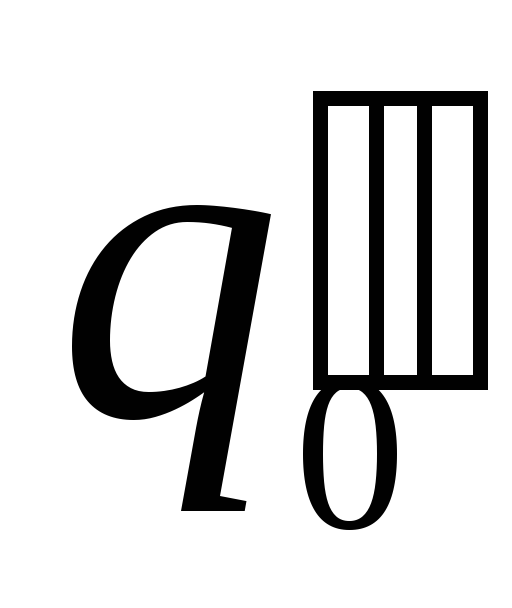 в одной и той же точке поля будут обладать
разной потенциальной энергией
в одной и той же точке поля будут обладать
разной потенциальной энергией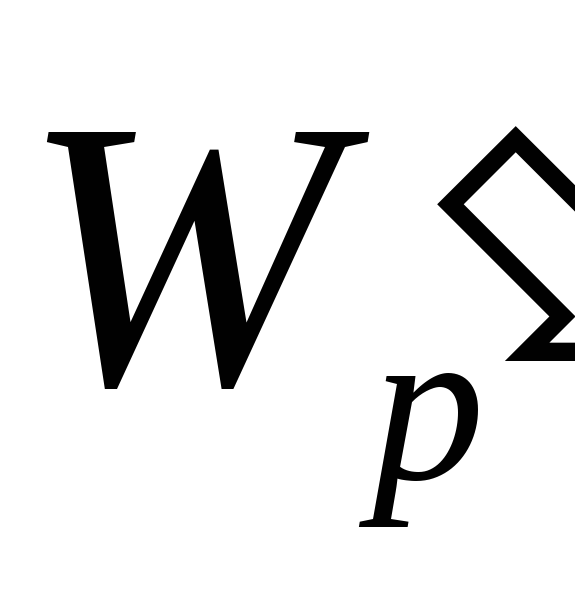 и
и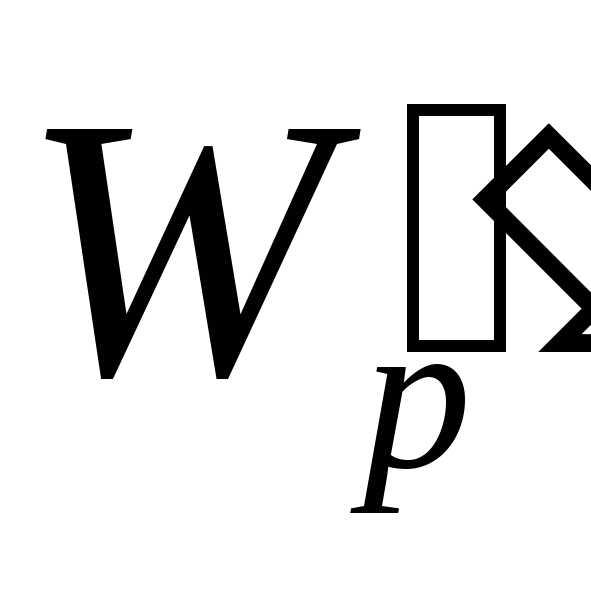 .
Однако отношение
.
Однако отношение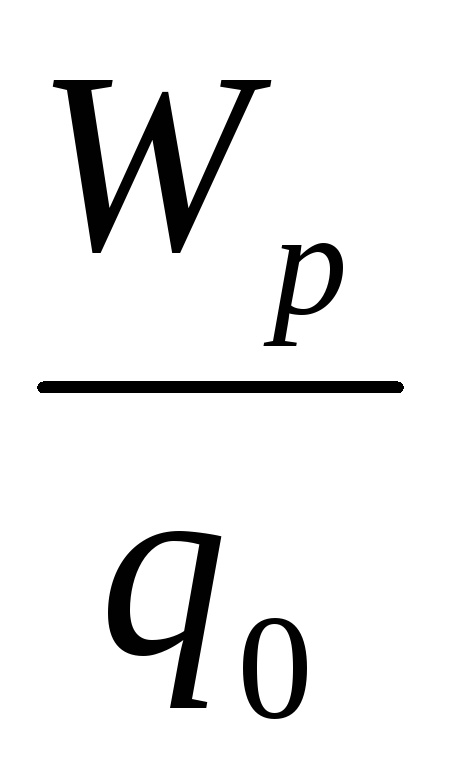 для всех пробных зарядов будет одинаково.
Величина
для всех пробных зарядов будет одинаково.
Величина
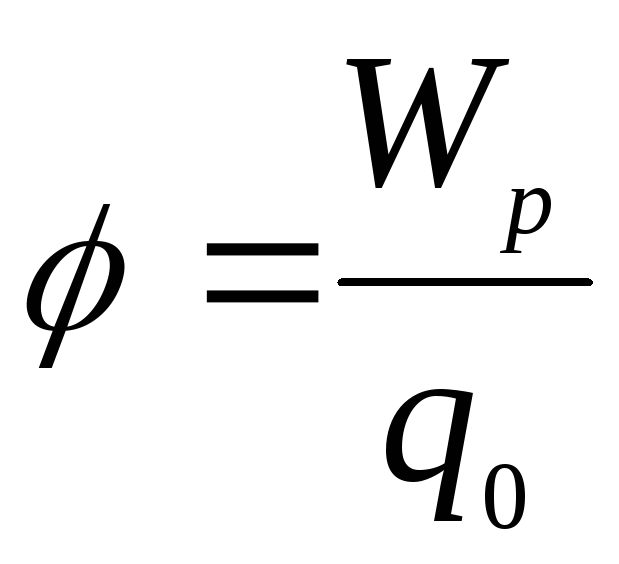
называется потенциалом электрического поля и является его энергетической характеристикой. Потенциал поля точечного заряда равен
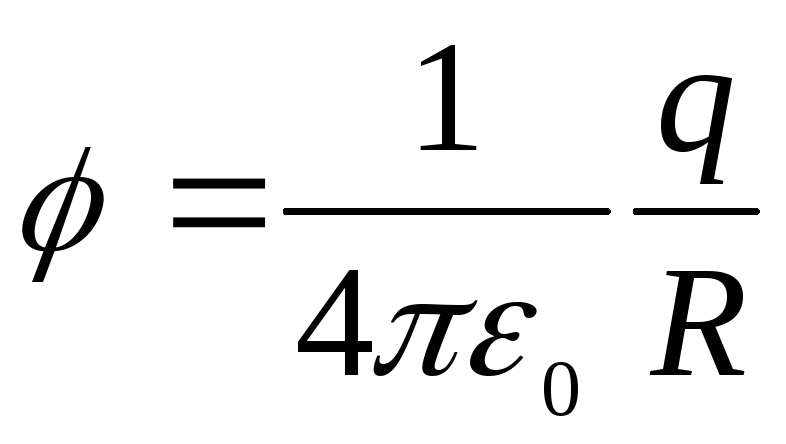 .
.
Если
поле создается системой
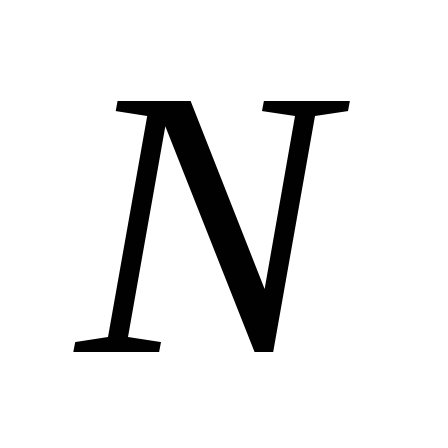 точечных зарядов, то
точечных зарядов, то
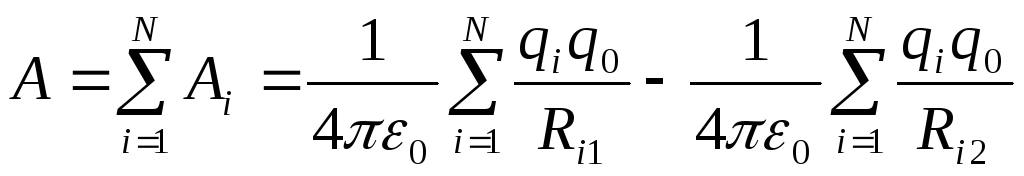 ,
,
где
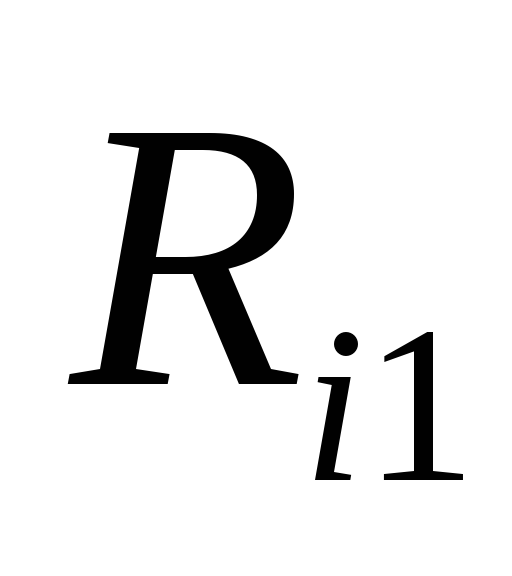 - расстояние от заряда
- расстояние от заряда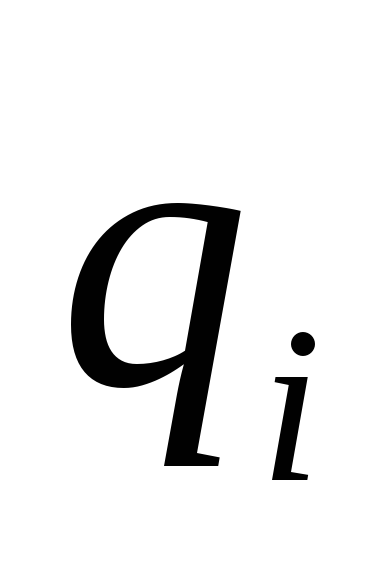 до начального положения заряда
до начального положения заряда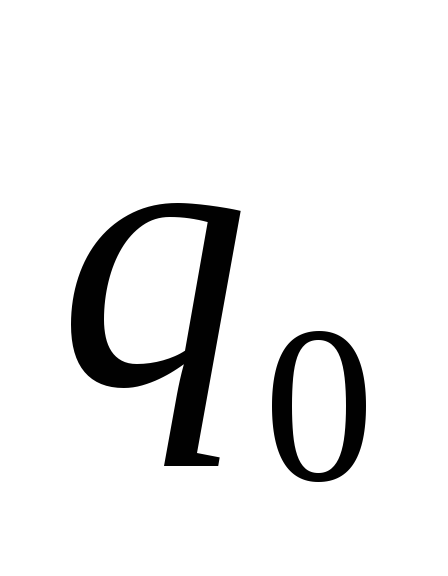 ,
,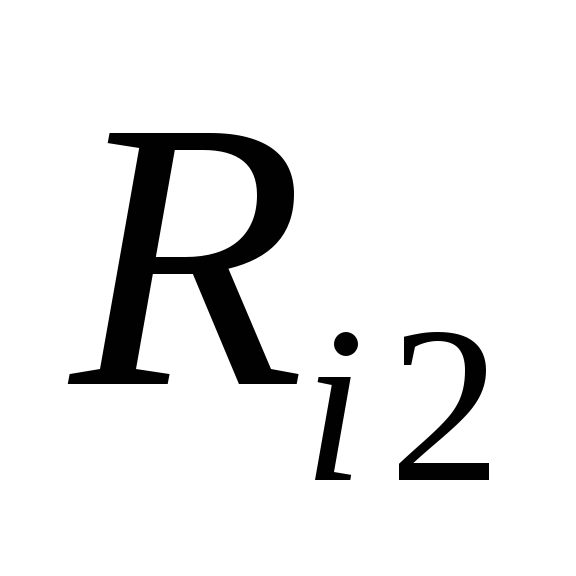 - расстояние от заряда
- расстояние от заряда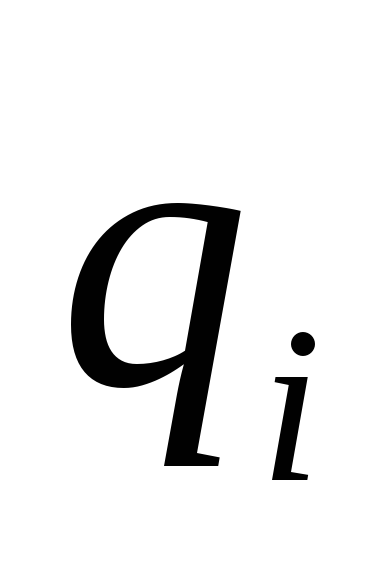 до конечного положения заряда
до конечного положения заряда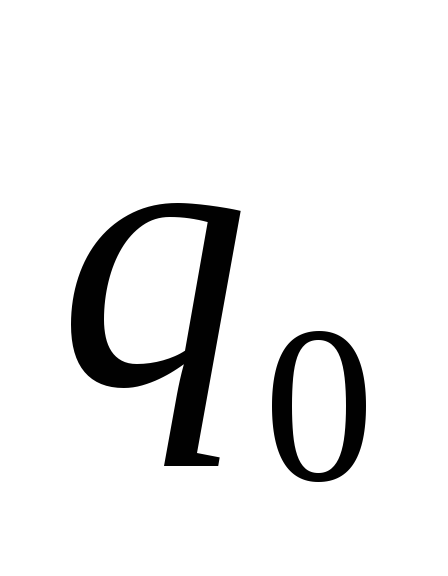 (заряд
(заряд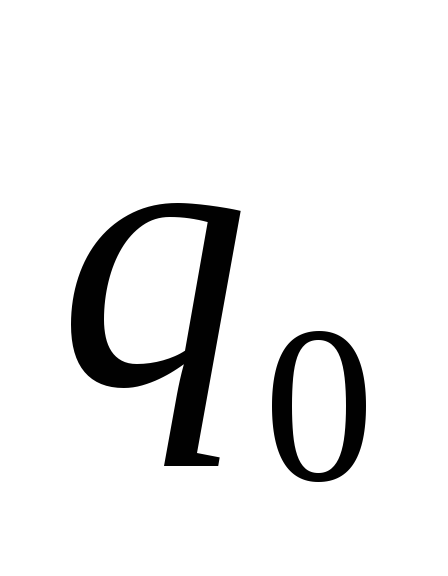 перемещается силами поля).
перемещается силами поля).
Тогда
потенциальная энергия заряда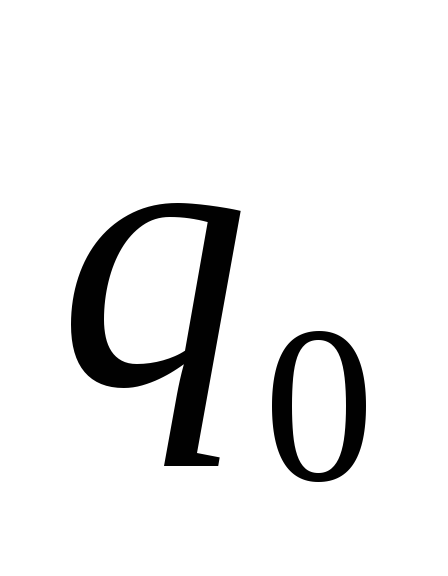 в поле системы зарядов:
в поле системы зарядов:
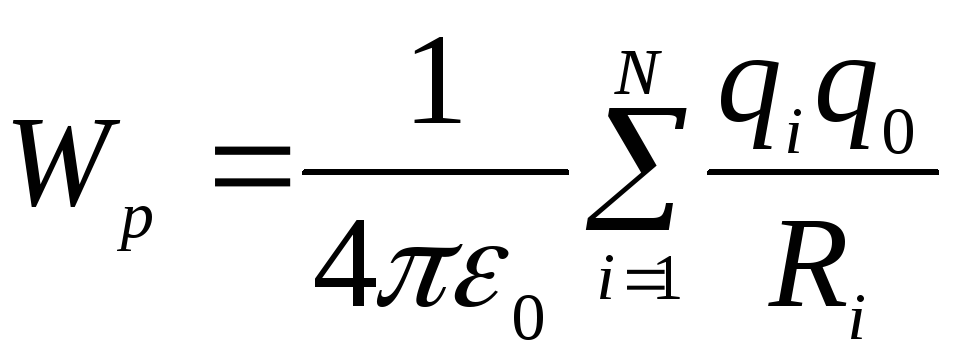 ,
,
а
потенциал
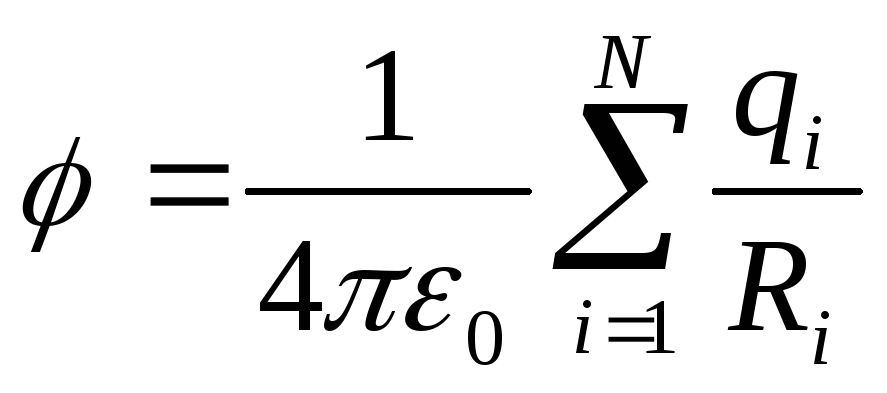
потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Зная
потенциал, можно найти потенциальную
энергию заряда
 в электрическом поле:
в электрическом поле:
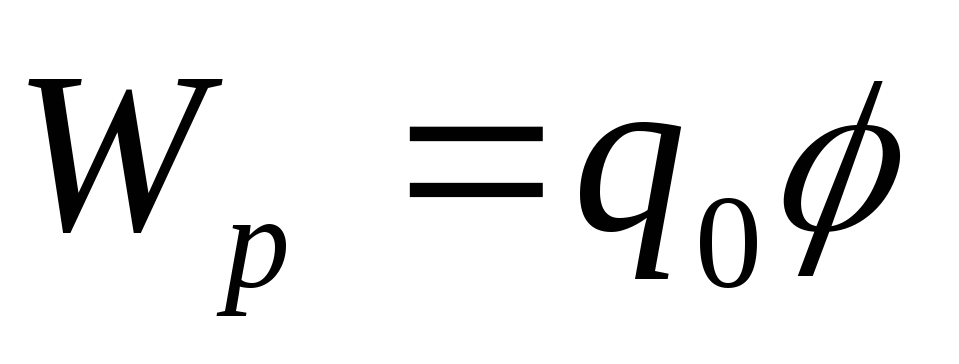 .
.
Работа поля над зарядом:
Работа равна убыли потенциала, умноженной на заряд.
Если заряд удаляется из точки на бесконечность, то работа сил поля равна
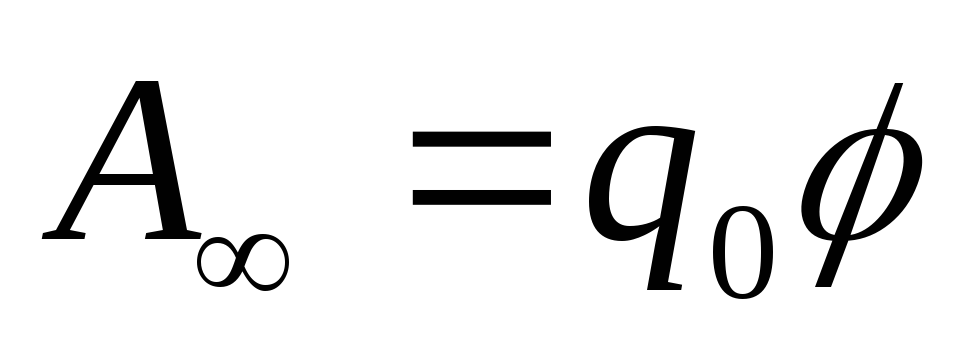
следовательно,
потенциал численно равен отношению
работы, которую совершают силы поля над
положительным зарядом при удалении его
из данной точки на бесконечность, к
величине этого заряда. Потенциал
измеряется в вольтах:
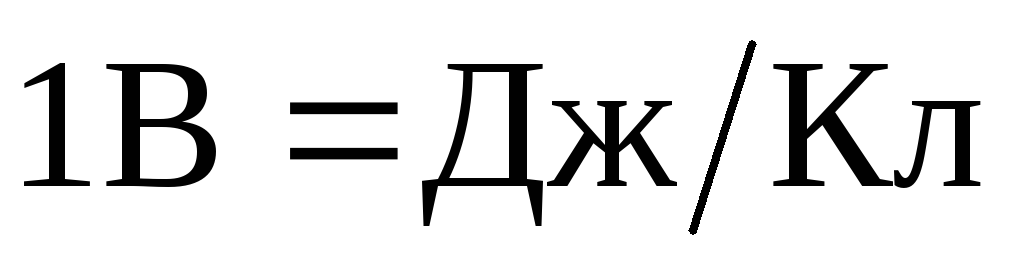 .
.
1.5.Связь между напряженностью и потенциалом
Электрическое
поле можно описывать либо с помощью
векторной величины
 (силовая характеристика), либо с помощью
скаляра
(силовая характеристика), либо с помощью
скаляра (энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
(энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
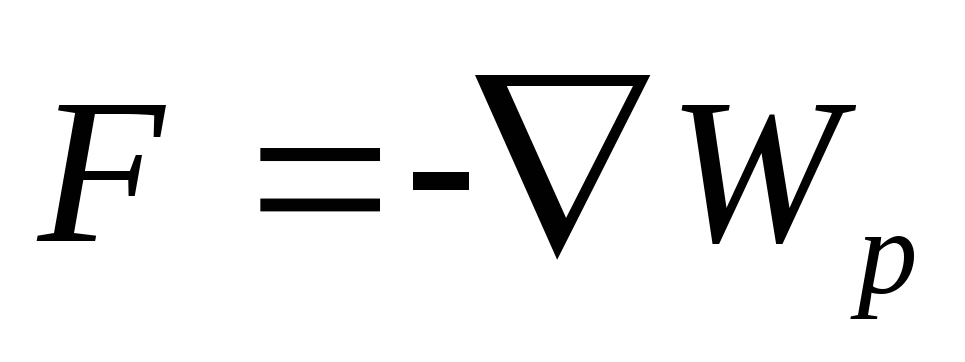 ,
,
где
 - оператор Набла,
- оператор Набла,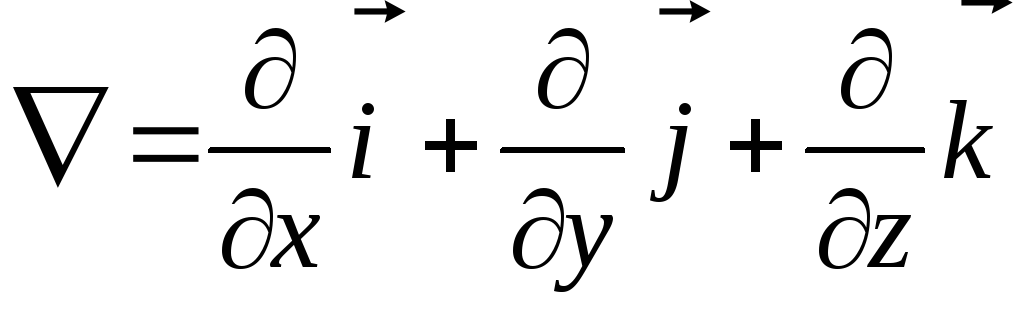 .
.
Для
заряженной частицы в электрическом
поле:
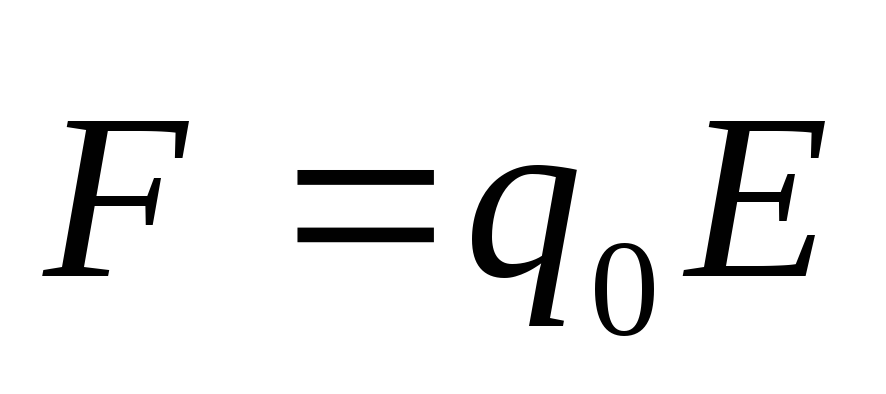 ,
,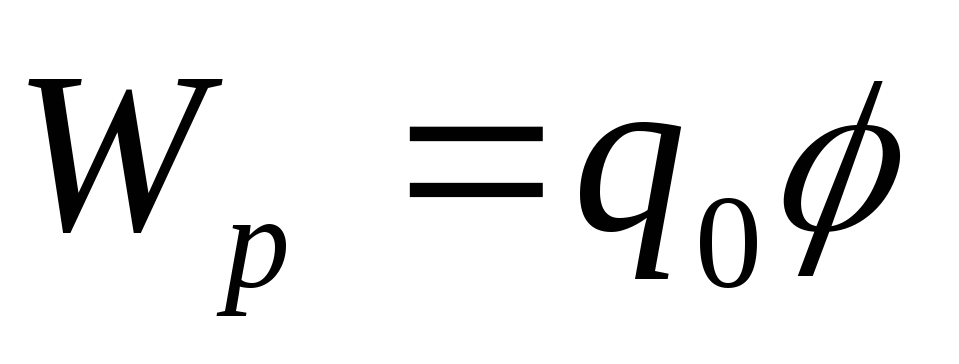 ,
тогда
,
тогда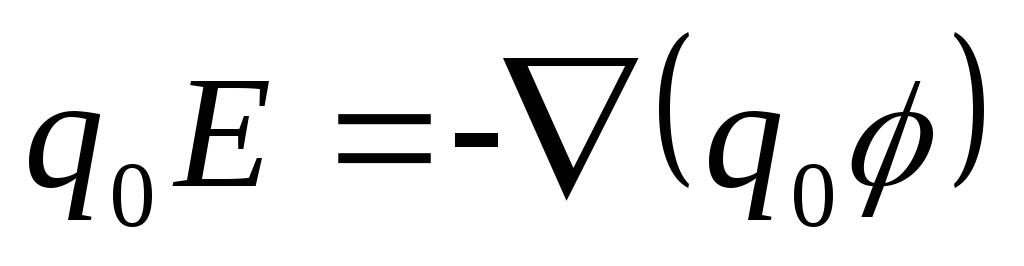 ,
, ,
тогда
,
тогда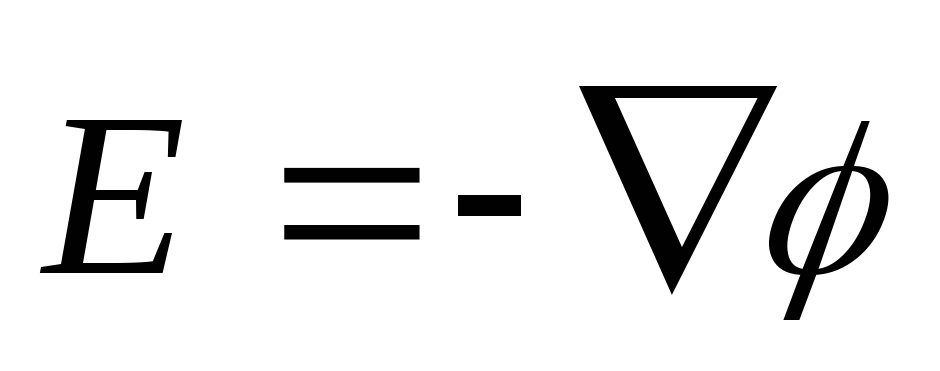 - связь напряженности и потенциала, или
- связь напряженности и потенциала, или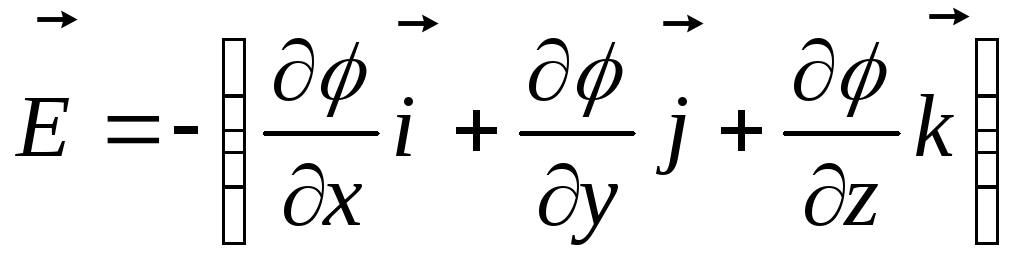 ,
или
,
или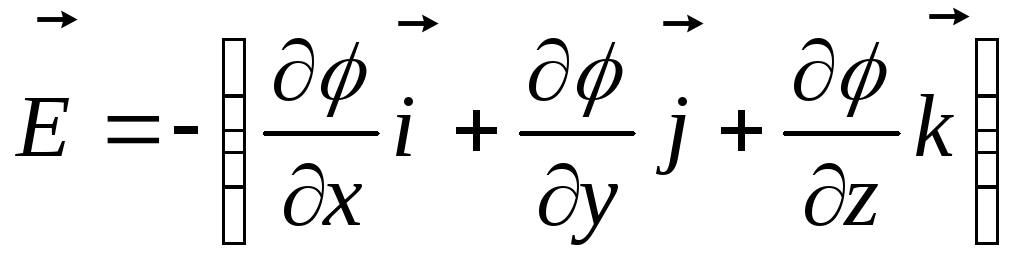 ,
или
,
или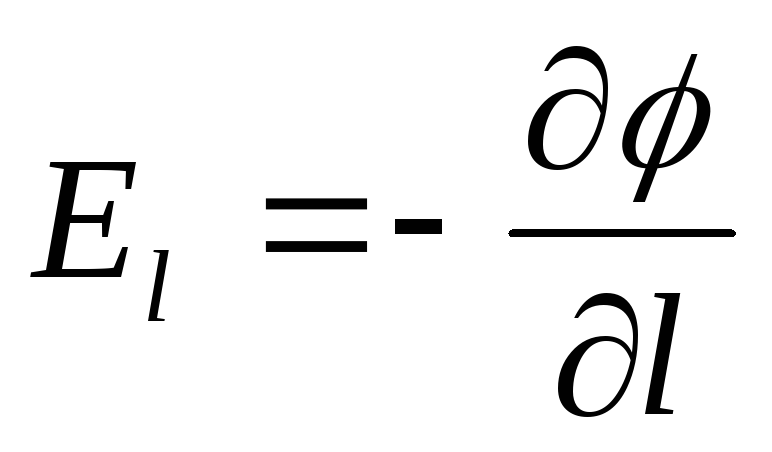 -
проекция
вектора
-
проекция
вектора
 на произвольное направление
на произвольное направление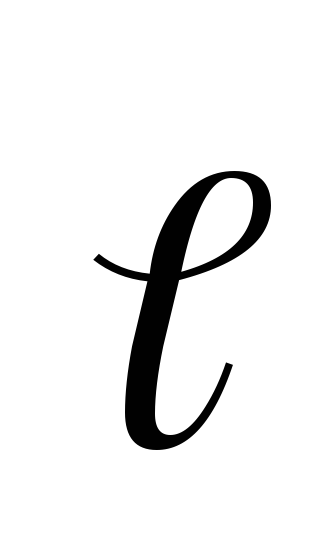 равна скорости убывания потенциала
равна скорости убывания потенциала вдоль направления
вдоль направления
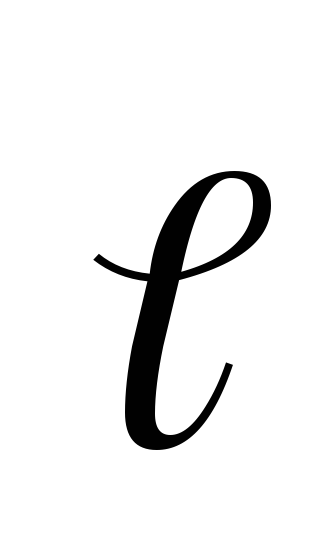 ,
или
,
или
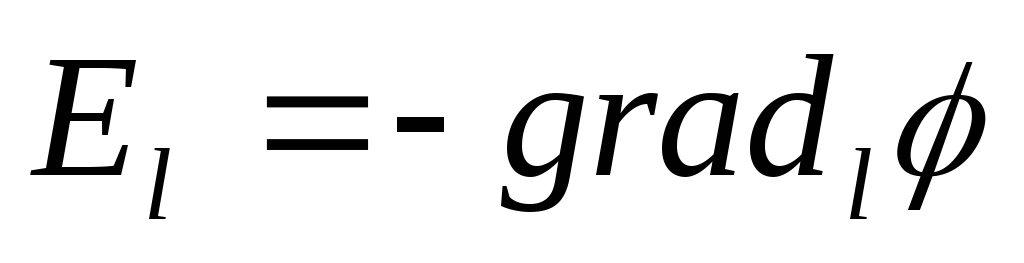 .
.
Так как градиент потенциала направлен в сторону его возрастания, а численная величина градиента является мерой быстроты этого возрастания, то можно сказать, что напряженность электрического поля есть мера быстроты спадания потенциала, или, просто, что она равна спаду потенциала.
Вернемся к
определению работы поля:
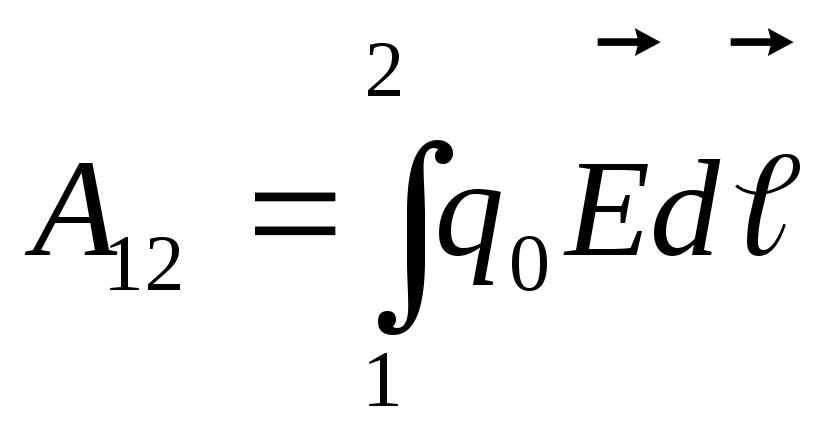 ,
,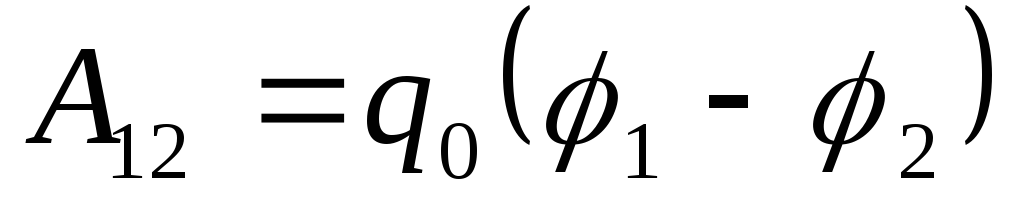 ,
отсюда циркуляция вектора
,
отсюда циркуляция вектора
 на
участке 1=2
равна
на
участке 1=2
равна
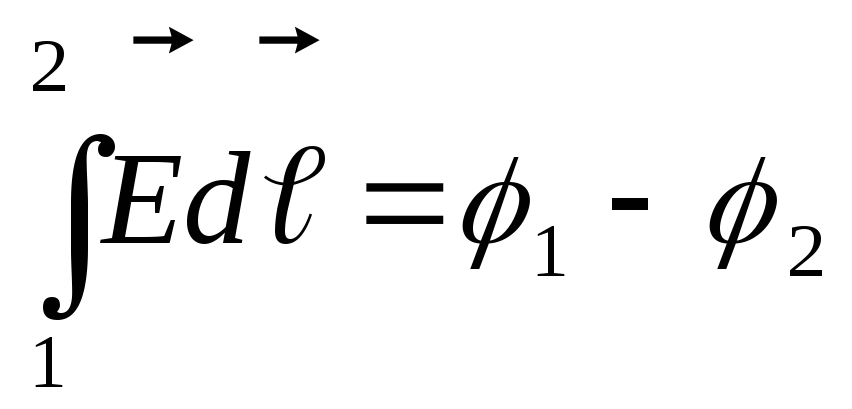 .
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
.
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
Для
обхода по замкнутому контуру:
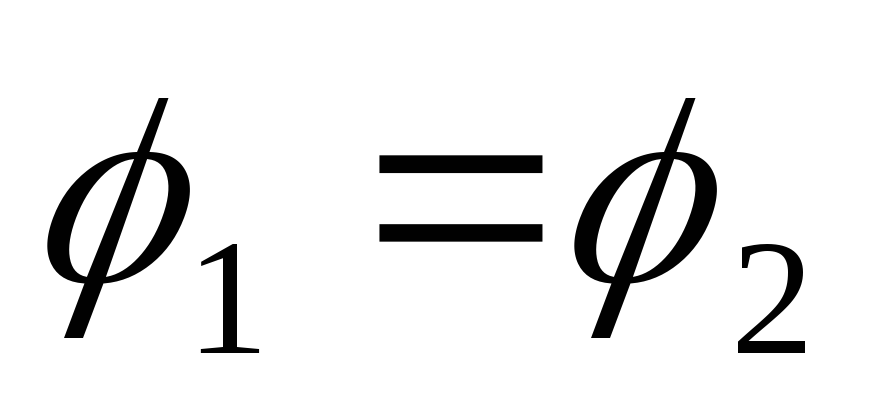 и
и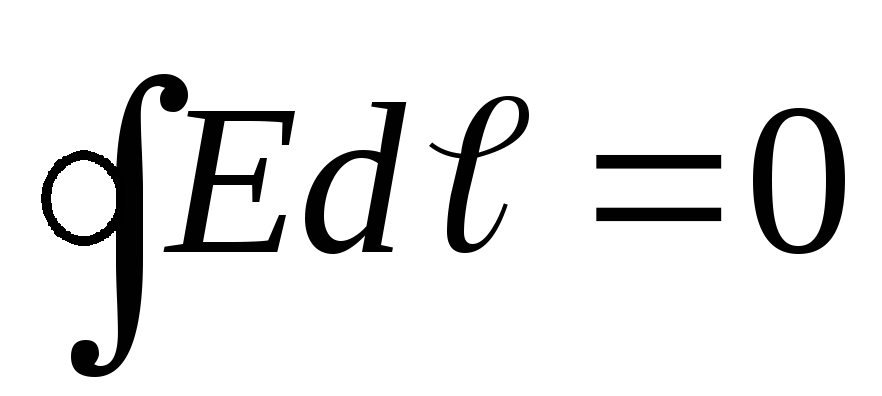 - пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
- пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
1.6. Эквипотенциальные поверхности
Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью:
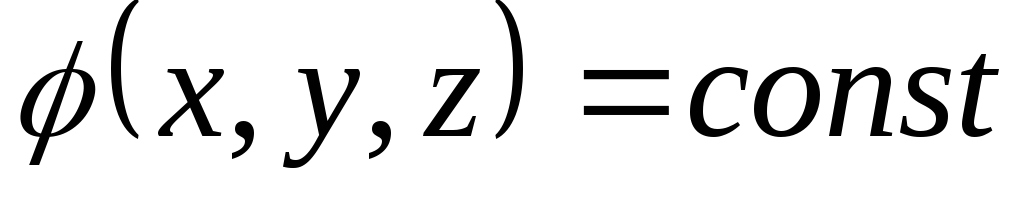
Уравнение эквипотенциальной поверхности.
При
перемещении по эквипотенциальной
поверхности на отрезок
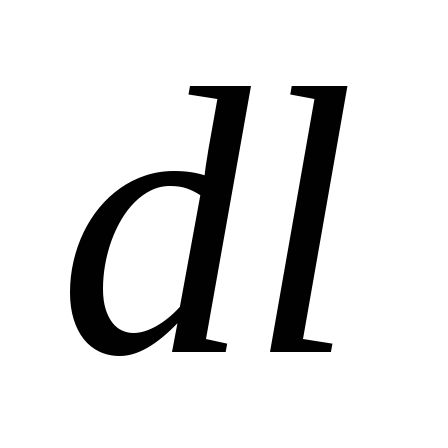 потенциал не изменяется
потенциал не изменяется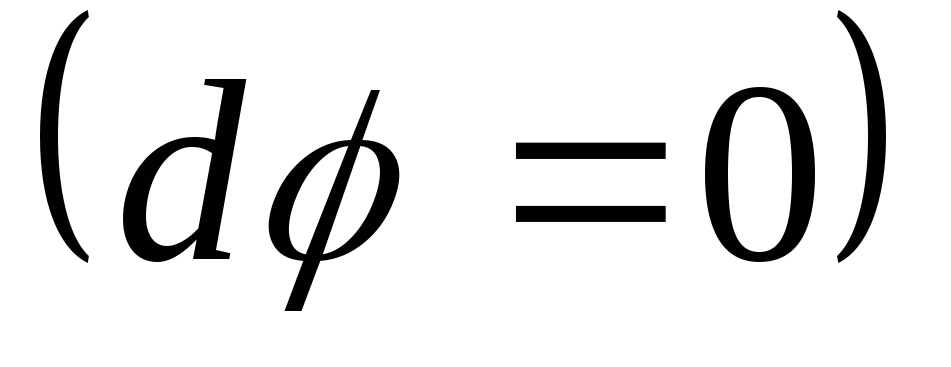 .
Таким образом, касательная к поверхности
составляющая вектора
.
Таким образом, касательная к поверхности
составляющая вектора равна нулю. Тогда вектор
равна нулю. Тогда вектор направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
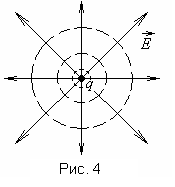 Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше
Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше ,
тем больше
,
тем больше .
.
Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.
Рассмотрим эквипотенциальную поверхность точечного заряда. Потенциал точечного заряда (рис.1.4)
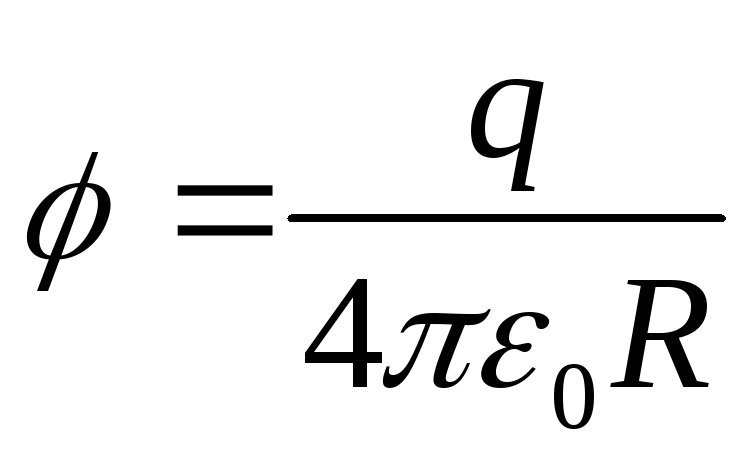 .
.
Таким
образом, эквипотенциальная поверхность
этого заряда будет сферой радиуса
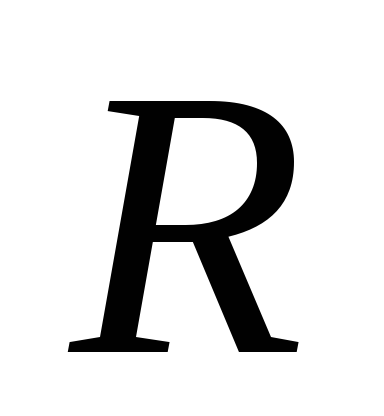 с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он
с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он
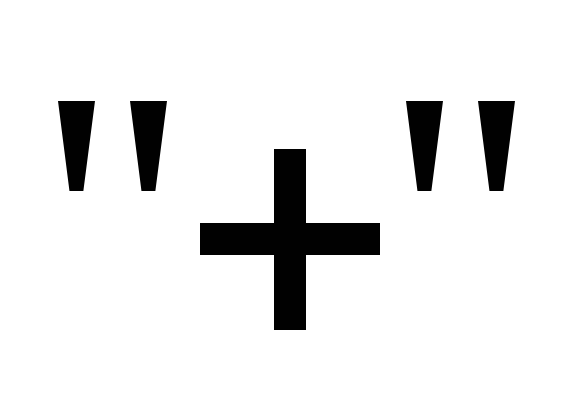 ,
или сходятся к заряду, если он “-”. То
есть вектор
,
или сходятся к заряду, если он “-”. То
есть вектор перпендикулярен эквипотенциальным
поверхностям.
перпендикулярен эквипотенциальным
поверхностям.
Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:
где W п1 и W п2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q , изменение потенциальной энергии равно
![]() .
.
При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r 1 и r 2 от заряда Q ,
Если поле создано системой точечных зарядов Q 1 , Q 2 ,¼ , Q n , то изменение потенциальной энергии заряда q в этом поле:
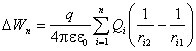 .
.
Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q , а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q , находящегося в электрическом поле, созданном другим точечным зарядом Q , получим
![]() ,
,
где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥ ), тогда постоянная C = 0 и предыдущее выражение принимает вид
При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную . В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q :
![]() .
.
Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q i (i = 1, 2, ... , n ). Энергия взаимодействия всех n зарядов определится соотношением
![]() ,
,
где r ij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.
Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля , определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W п / q , откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).
Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e :
Принцип суперпозиции. Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q 1, Q 2 ¼ , Q n имеем
![]() ,
,
где r i - расстояние от точки поля, обладающей потенциалом j , до заряда Q i . Если заряд произвольным образом распределен в пространстве, то
![]() ,
,
где r - расстояние от элементарного объема dx , dy , dz до точки (x , y , z ), где определяется потенциал; V - объем пространства, в котором распределен заряд.
Потенциал и работа сил электрического поля.
Основываясь на определении потенциала, можно показать, что работа
сил электрического поля при перемещении точечного заряда q
из одной точки поля в другую равна произведению величины этого заряда
на разность потенциалов в начальной и конечной точках пути, A
=
q
(j
1
-
j
2
)
.
Если по аналогии с потенциальной энергией считать, что в точках,
бесконечно удалённых от электрических зарядов - источников поля, потенциал
равен нулю, то работу сил электрического поля при перемещении заряда q
из точки 1 в бесконечность можно представить как A
¥
=
q
j
1 .
Таким образом, потенциал â данной точке электростатического
поля - это физическая величина, численно равная работе,
совершаемой силами электрического поля при перемещении единичного положительного
точечного заряда из данной точки поля в бесконечно удаленную
: j
= A
¥
/ q
.
В некоторых случаях потенциал электрического поля нагляднее определяется
как физическая величина, численно равная работе
внешних сил против сил электрического поля при перемещении единичного
положительного точечного заряда из бесконечности в данную точку
. Последнее
определение удобно записать следующим образом:
В современной науке и технике, особенно при описании явлений, происходящих в микромире, часто используется единица работы и энергии, называемая электрон-вольтом (эВ). Это работа, совершаемая при перемещении заряда, равного заряду электрона, между двумя точками с разностью потенциалов 1 В: 1 эВ = 1,60× 10 - 1 9 Кл× 1 В = 1,60× 10 - 1 9 Дж.
Вопросы
1) Дайте определение потенциала данной точки поля и разности потенциалов двух точек поля.
2) Приведите графики зависимостей напряженности поля и потенциала от расстояния для равномерно заряженной сферической поверхности. Дайте их объяснение и обоснование.



