Курс лекций по физике стоячие волны. Образовательный портал тгу
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн по отдельности. Это вытекающее из опыта утверждение называется принципом суперпозиции (наложения) волн .
В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, волны называются когерентными. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга. Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной.
Стоячая волна - это волна, которая образуется при наложении двух волн с одинаковой амплитудой и частотой, когда волны движутся навстречу друг другу.
Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна налагаясь друг на друга, дают стоячую волну.
Напишем уравнения двух плоских волн, распространяющихся вдоль оси x в противоположных направлениях:
Сложив эти уравнения и преобразовав результат по формуле для суммы косинусов, получим:
Чтобы
упростить это уравнение, выберем начало
отсчета x
так, чтобы разность
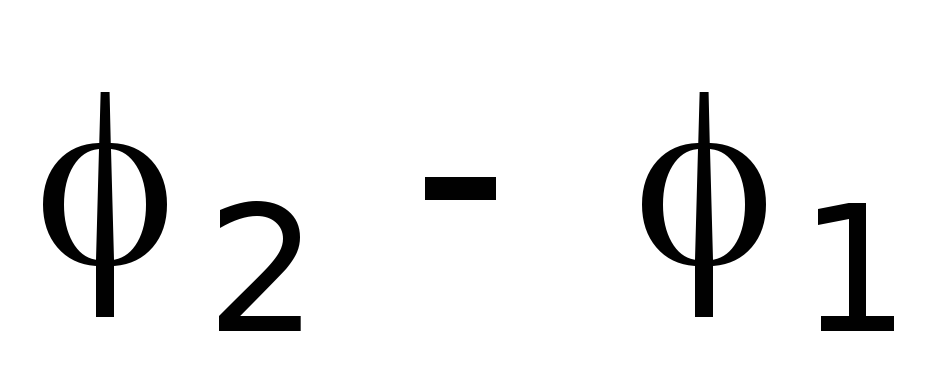 стала равной нулю, а начало отсчета t
- так, чтобы оказалась равной нулю сумма
стала равной нулю, а начало отсчета t
- так, чтобы оказалась равной нулю сумма
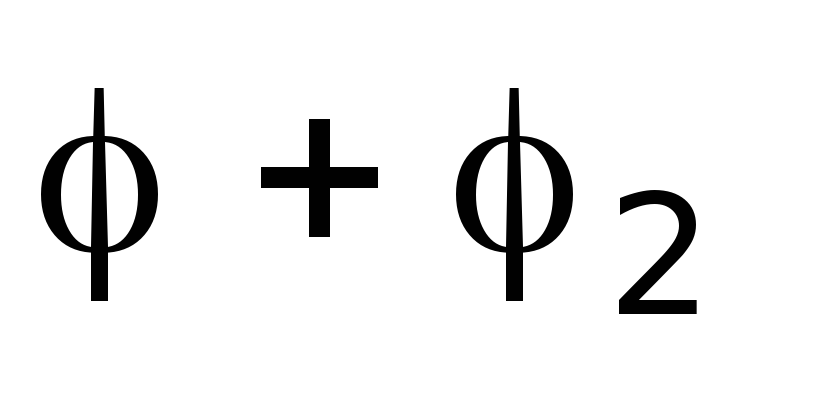 .Тогда
.Тогда
- уравнение стоячей волны .
Заменив
волновое число к
его
значением
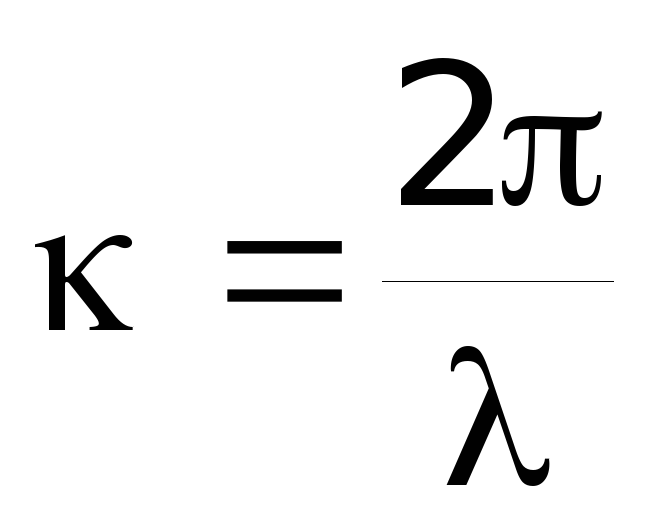 ,
получим
уравнение стоячей волны,
удобное для анализа колебаний частиц
в стоячей волне:
,
получим
уравнение стоячей волны,
удобное для анализа колебаний частиц
в стоячей волне:
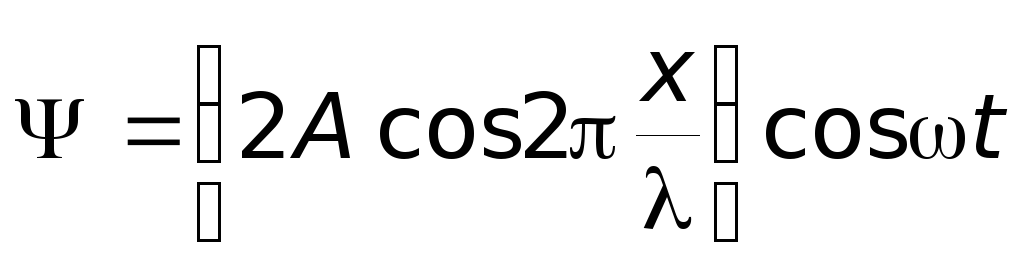 .
.
Из этого уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда колебаний зависит от x :
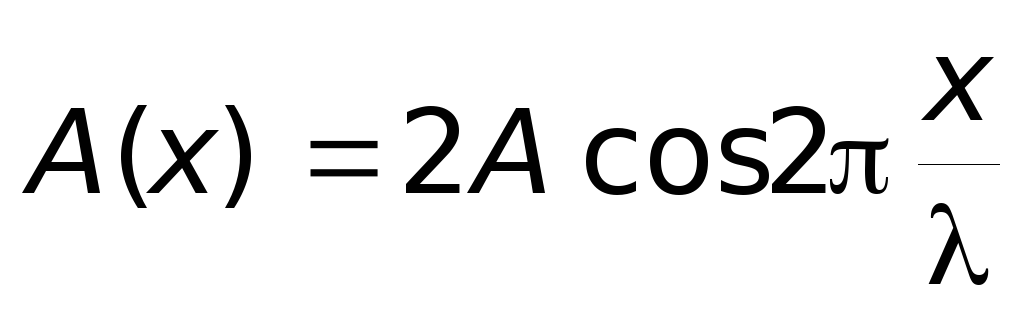 .
.
В точках, координаты которых удовлетворяют условию
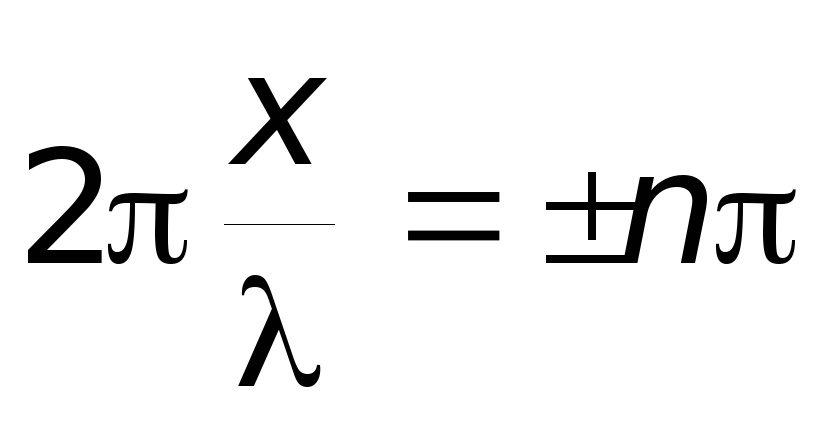
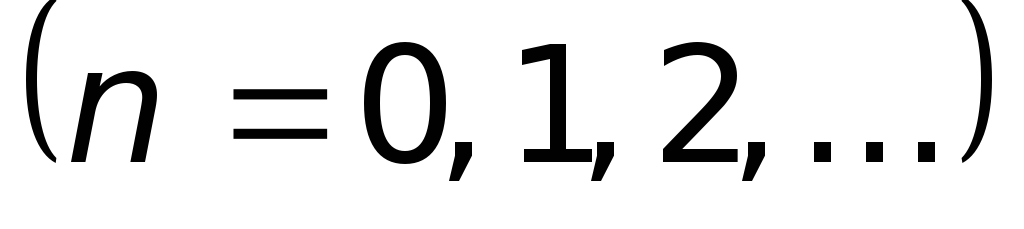 ,
,
амплитуда колебаний достигает максимального значения. Эти точки называются пучностями стоячей волны. Значения координат пучностей равны:
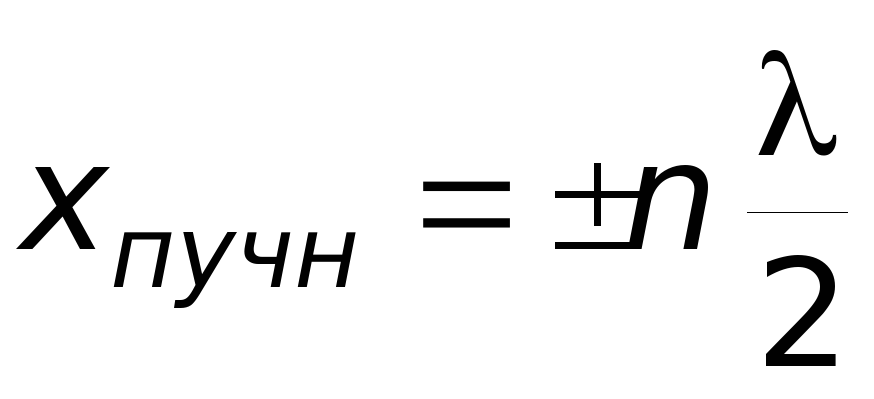
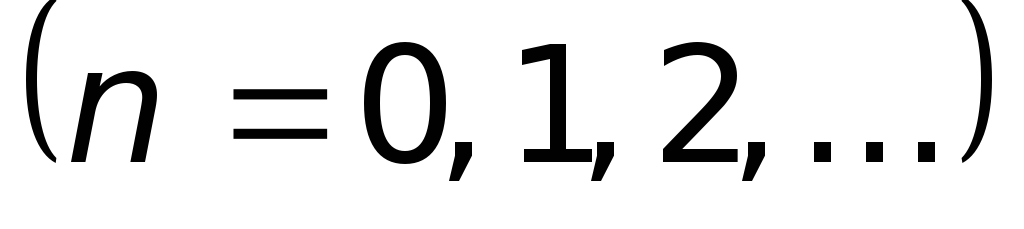 .
.
В точках, координаты которых удовлетворяют условию:
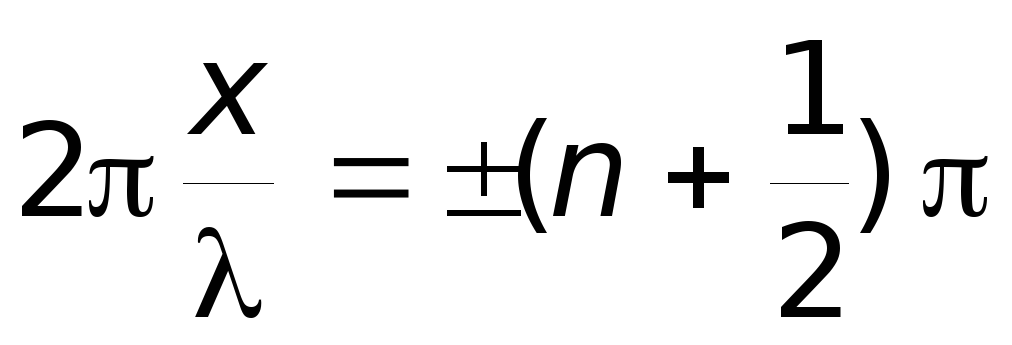
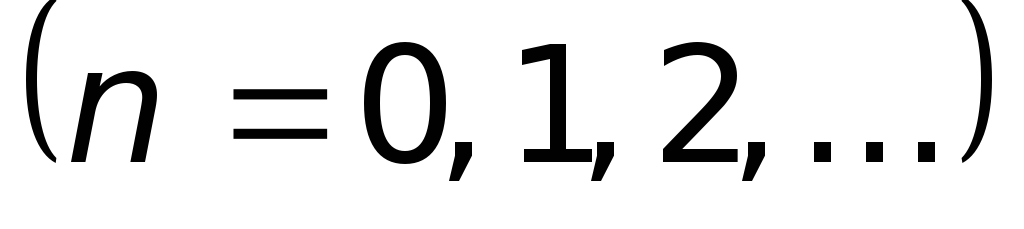 ,
,
амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют значения:
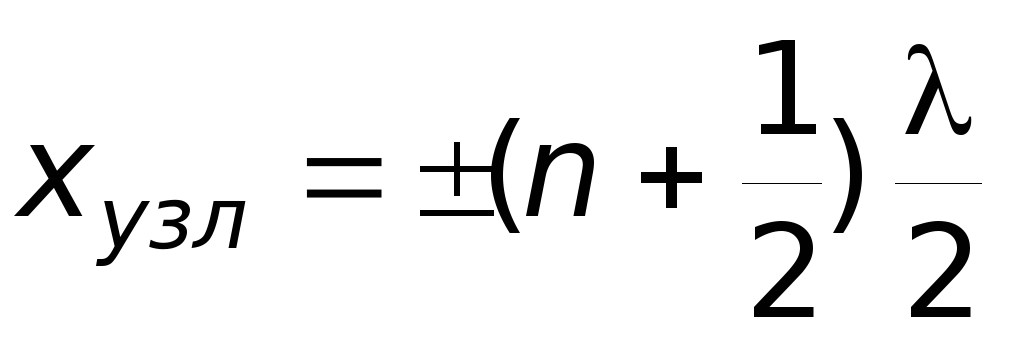
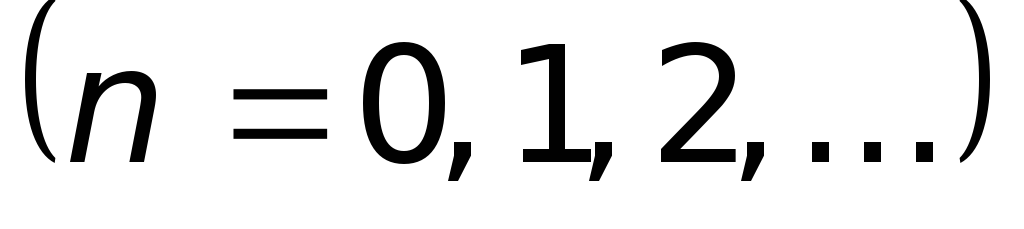 .
.
Из этих формул следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно . Пучности и узлы сдвинуты друг относительно друга на четверть длины волны.
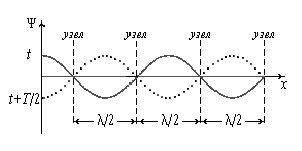
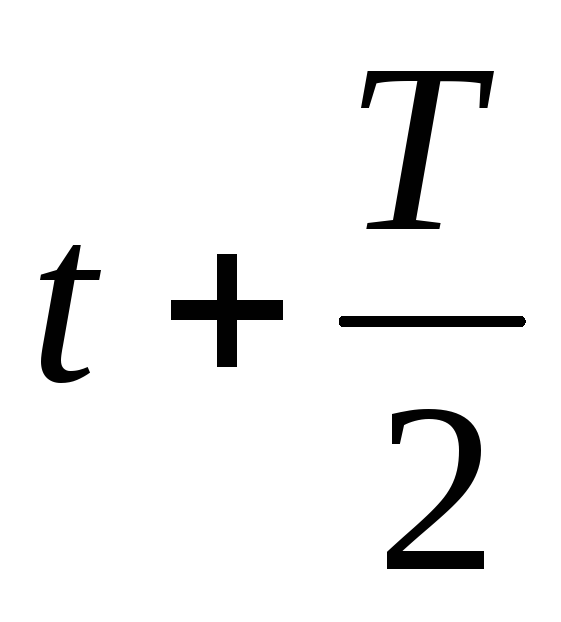 (пунктирная кривая). Как видно из рисунка
точки, лежащие по разные стороны от
узла, колеблются в противофазе. Все
точки, заключенные между двумя соседними
узлами, колеблются синфазно (т.е. в
одинаковой фазе).
(пунктирная кривая). Как видно из рисунка
точки, лежащие по разные стороны от
узла, колеблются в противофазе. Все
точки, заключенные между двумя соседними
узлами, колеблются синфазно (т.е. в
одинаковой фазе).Стоячая волна не переносит энергию. Дважды за период происходит превращение энергии стоячей волны то полностью в потенциальную, сосредоточенную в основном вблизи узлов волны, то полностью в кинетическую, сосредоточенную в основном вблизи пучностей волны. В результате происходит переход энергии от каждого узла к соседним пучностям и обратно. Средний по времени поток энергии в любом сечении волны равен нулю.
Стоячие волны образуются при наложении двух одина-ковых волн, бегущих навстречу друг другу. Все, наверное, ви-дели стоячие волны в гитарных струнах. Когда в каком-либо месте оттягивают и отпускают струну, в разные стороны на-чинают разбегаться упругие поперечные волны, которые за-тем отражаются от концов струны и, накладываясь друг на друга, образуют стоячие волны (если при распространении и отражении нет затухания). Как это происходит?
При сложе-нии двух синусоидальных волн с одинаковыми частотой и ам-плитудой, но распространяющихся в разных направлениях оси x, получаем возмущение, которое описывается функцией
F(x, t) = f 0 sin(ωt — kx + φ 1) + f 0 sin(ωt + kx + φ 2) = 2 f 0 cos(kx + (φ 2 — φ 1) / 2) + (φ 1 + φ 2) / 2).
Это и есть уравнение стоячей волны . В каждой точке стоя-чей волны колебания осуществляются по гармоническому закону:
F(x, t) = F 0 sin (ωt + (φ 1 + φ 2) / 2.
Амплитуда колеба-ний
| F 0 | = 2 f 0 | cos(kx + (φ 2 — φ 1) / 2)|
зависит от координа-ты x . В точках, где kx + Δφ / 2 = (n + 1 / 2)π (n — целое чис-ло, Δφ = φ 1 — φ 2), амплитуда F 0 = 0. Такие точки называют узлами стоячей волны , колебания в них отсутствуют. Точ-ки, для которых амплитуда колебаний | F 0 | = 2 f 0 максималь-на, называют пучностями стоячей волны . Расстояние Δx между соседними узлами (или соседними пучностями) рав-но половине длины бегущих волн, из которых образовалась стоячая волна:
Δx = π / k = λ / 2.
В точках между двумя соседними узлами колебания проис-ходят в одинаковой фазе, а амплитуда изменяется от нуля до максимума (в пучности, которая расположена посереди-не между узлами) и опять до нуля. Материал с сайта
При переходе через узел фаза колебаний изменяется на π, так как меняется знак F 0 . В стоячей волне возмущение сре-ды обращается в нуль одновременно во всех точках, и одно-временно во всех точках возмущение достигает максималь-ного по величине значения. Так, звучащая струна через каждый полупериод выпрямляется, а через четверть перио-да после выпрямления принимает «наиболее изогнутую» форму.
Если наблюдать колебания только в одной точке, то невозможно сказать, какая волна — бегущая или стоя-чая — вызвала эти колеба-ния. Но если следить за ко-лебаниями в нескольких точках, то картины колеба-ний в бегущей и стоячей волнах будут совершенно различны. В плоской бегу-щей волне колебания в разных точках происхо-дят с одинаковой амплиту-дой, но в различных фазах. В стоячей волне колебания в разных точках происхо-дят с разными амплитуда-ми, но в одинаковой фазе. Поэтому при наблюдении «целой картины» спутать бегущую и стоячую волны, конечно, невозможно.
На этой странице материал по темам:
Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудойОчень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная, налагаясь друг на друга, дают стоячую волну.
Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях:
Складывая вместе оба уравнения и преобразовывая результат по формуле для суммы косинусов, получаем:
Заменив волновое число k его значением выражению для можно придать следующий вид:
амплитуда колебаний достигает максимального значений 2а . Эти точки называются пучностями стоячей волны. Из условия (84.2) получаются значения координат пучностей:
Из формул (84.3) и (84.4) следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно . Пучности и узлы сдвинуты друг относительно друга на четверть длины волны.
Обратимся снова к уравнению (84.1). Множитель при переходе через нулевое значение меняет знак. В соответствии с этим фаза колебаний по разные стороны от узла отличается на , т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе. Все точки, заключенные между двумя соседними узлами, колеблются синфазно (т.е. в одной и той же фазе).(84.6)
Уравнение (84.5) описывает стоячую волну деформации, а (84.6) - стоячую волну скорости. Из вида этих уравнении следует, что узлы и пучности скорости совпадают с узлами и пучностями смещения; узлы же и пучности деформации совпадают соответственно с пучностями и узлами скорости и смещения (рис. 205).
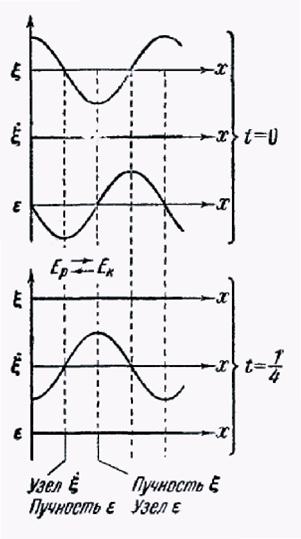
В то время, как и достигают максимальных значений, обращается в нуль, и наоборот. Соответственно дважды за период происходит превращение энергии стоячей волны то полностью в потенциальную, сосредоточенную в основном вблизи узлов волны (где находятся пучности деформации), то полностью в кинетическую, сосредоточенную в основном вблизи пучностей волны (где находятся пучности скорости). В результате происходит переход энергии от каждого узла к соседним с ним пучностям и обратно. Средний поток энергии в любом сечении волны равен нулю.
Стоячие волны образуются в результате интерференции двух встречных плоских волн одинаковой частоты ω и амплитуды А.
Представим себе, что в точке S (рис.7.4) находится вибратор, от которого вдоль луча SO распространяется плоская волна. Достигнув преграды в точке О, волна отразится и пойдёт в обратном направлении, т.е. вдоль луча распространяются две бегущие плоские волны: прямая и обратная. Эти две волны когерентны, так как рождены одним и тем же источником и, накладываясь друг на друга, будут интерферировать между собой.
Возникающее в результате интерференции колебательное состояние среды и называется стоячей волной.
Запишем уравнение прямой и обратной бегущей волны:
прямая -
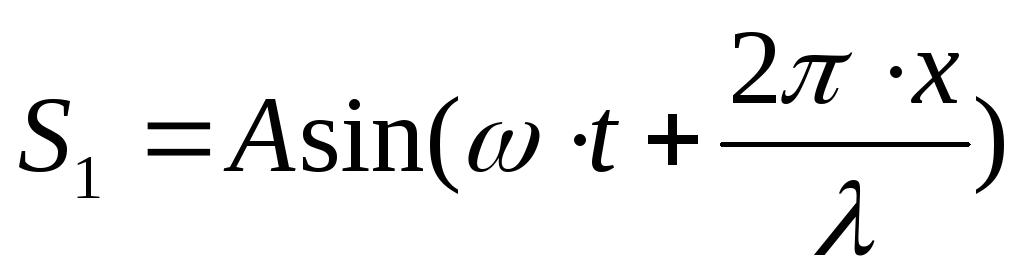 ;обратная
-
;обратная
-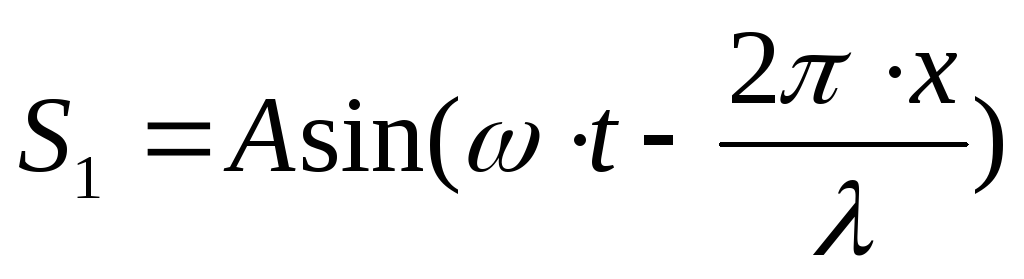
где S 1 и S 2 – смещение произвольной точки на луче SO. С учётом формулы для синуса суммы результирующее смещение равно
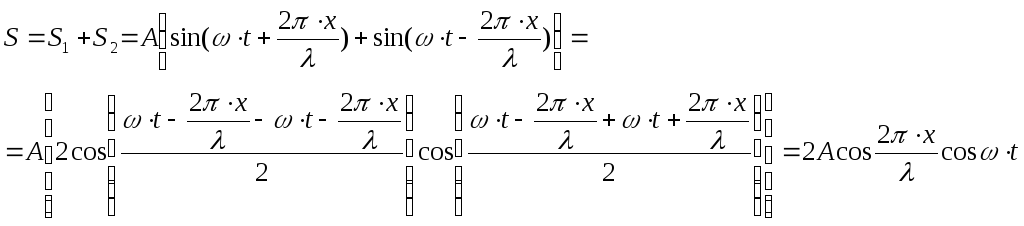
Таким образом, уравнение стоячей волны имеет вид
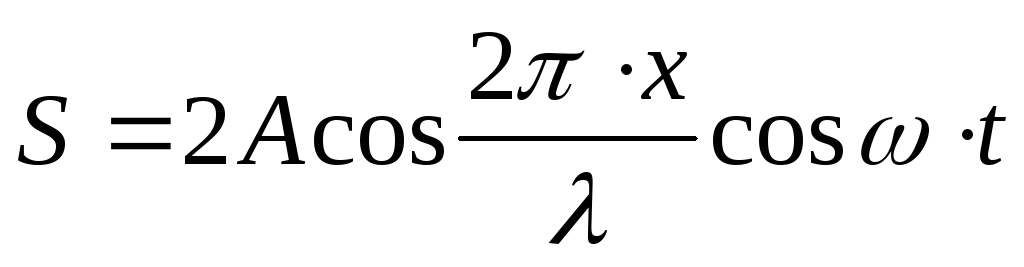 (7.17)
(7.17)
Множитель cosωt
показывает, что все точки среды на луче
SО совершают простые гармонические
колебания с частотой
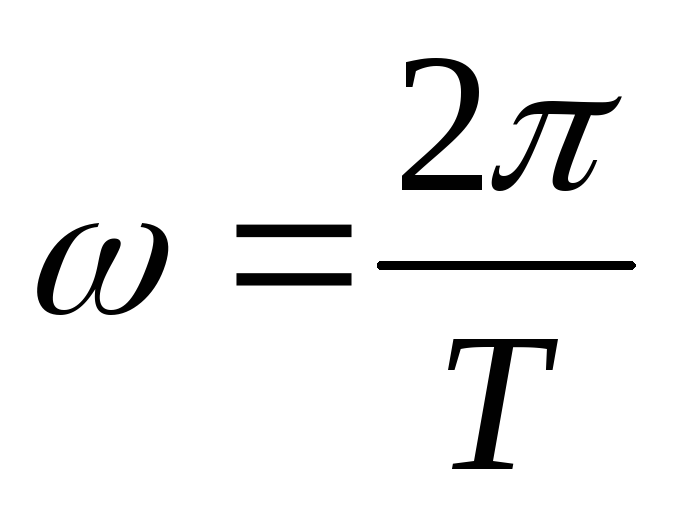 .
Выражение
.
Выражение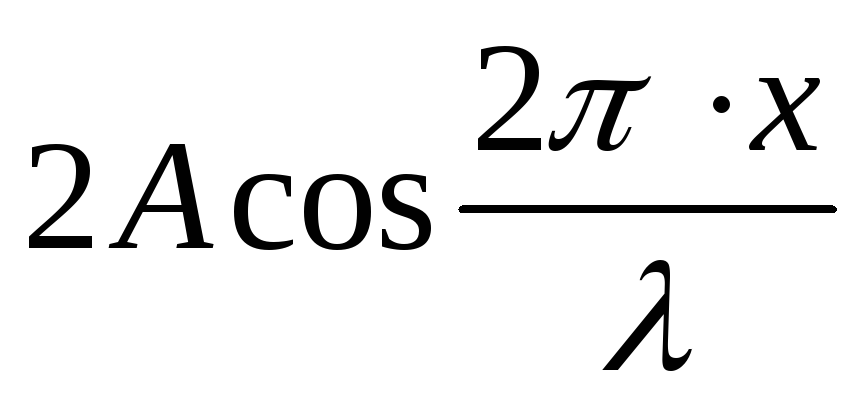 называется амплитудой стоячей волны.
Как видно, амплитуда определяется
положением точки на лучеSO
(х).
называется амплитудой стоячей волны.
Как видно, амплитуда определяется
положением точки на лучеSO
(х).
Максимальное значение амплитуды будут иметь точки, для которых
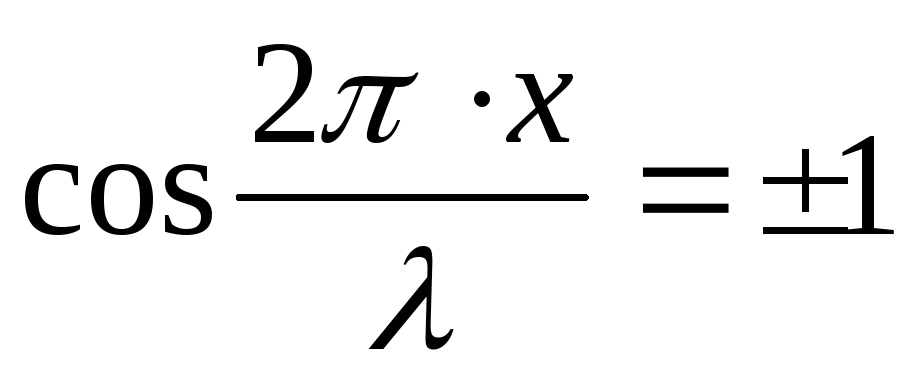 или
или
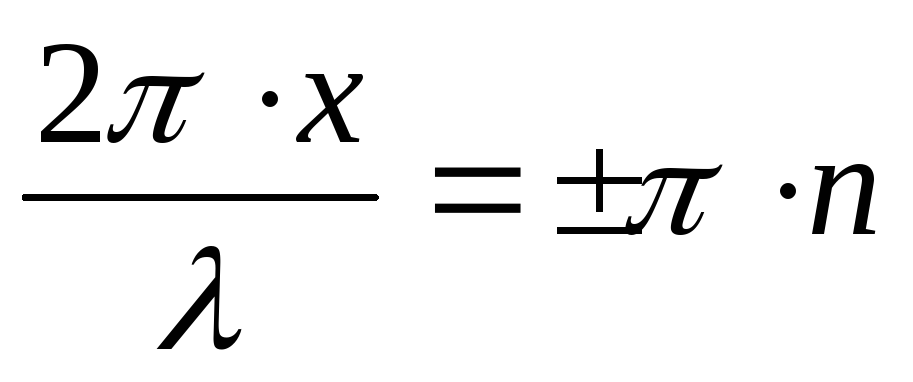 (n
= 0, 1, 2,….)
(n
= 0, 1, 2,….)
откуда
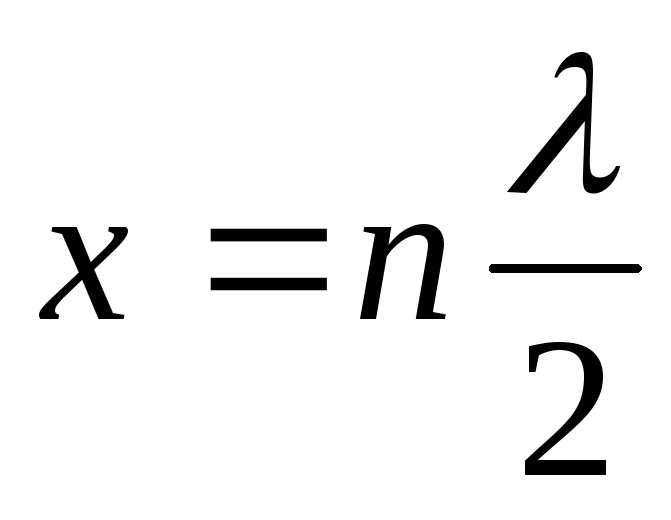 ,
или
,
или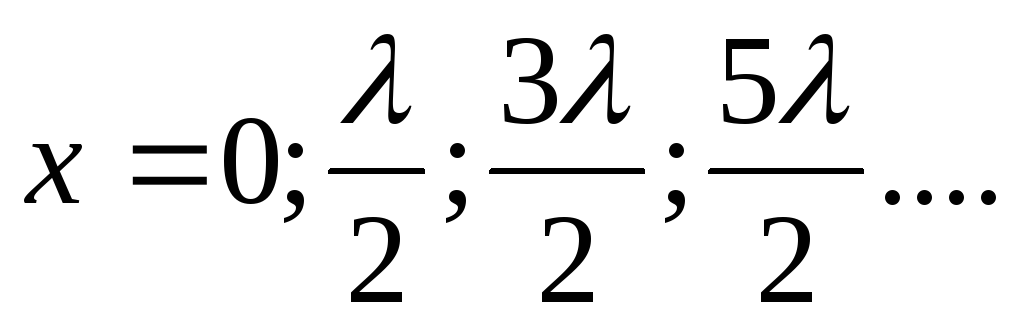 (7.18)
(7.18)
пучностями стоячей волны .
Минимальное значение , равное нулю, будут иметь те точки для которых
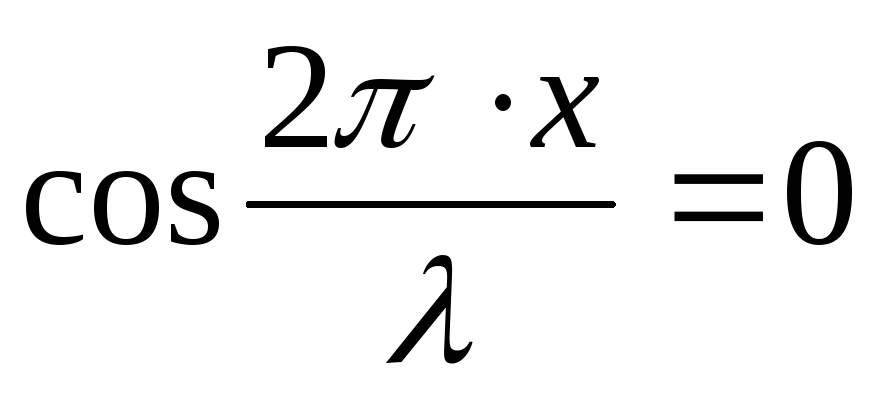 или
или
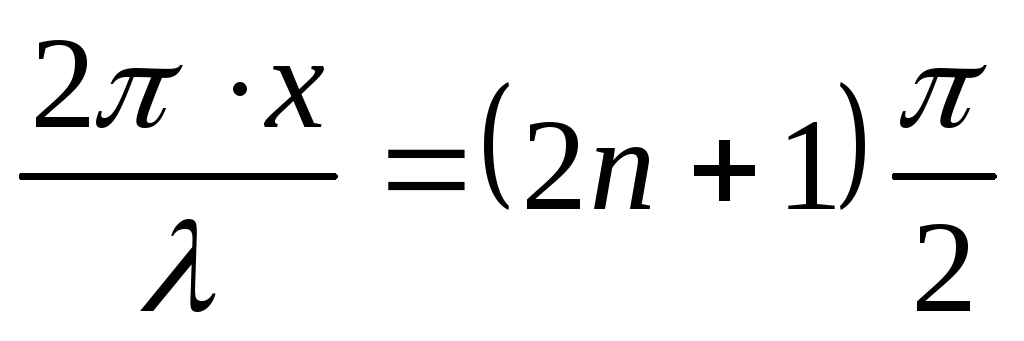 (n
= 0, 1, 2,….)
(n
= 0, 1, 2,….)
откуда
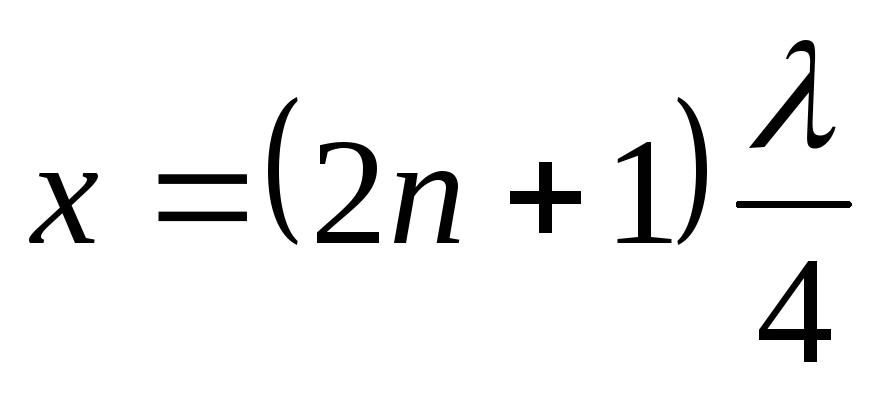 или
или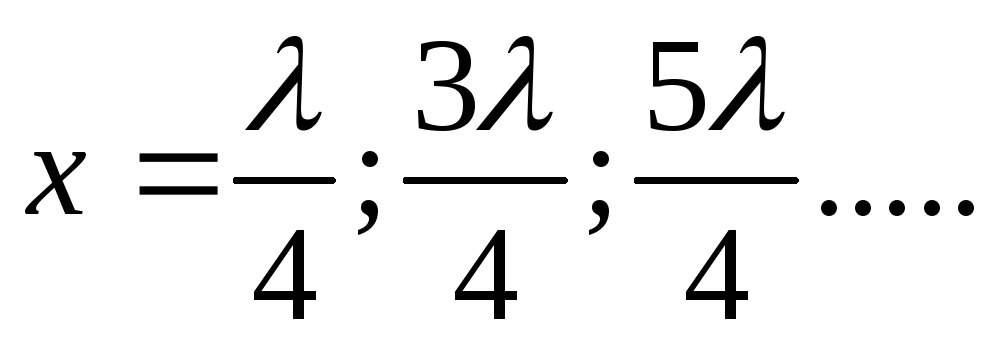 (7.19)
(7.19)
Точки, имеющие такие координаты, называют узлами стоячей волны . Сопоставляя выражения (7.18) и (7.19), видим, что расстояние между соседними пучностями и соседними узлами равно λ/2.
Н а
рисунке сплошной линией изображено
смещение колеблющихся точек среды в
некоторый момент времени, пунктирной
кривой – положение этих же точек через
Т/2. Каждая точка совершает колебания с
амплитудой, определяемой её расстоянием
от вибратора (х).
а
рисунке сплошной линией изображено
смещение колеблющихся точек среды в
некоторый момент времени, пунктирной
кривой – положение этих же точек через
Т/2. Каждая точка совершает колебания с
амплитудой, определяемой её расстоянием
от вибратора (х).
В отличие от бегущей волны в стоячей волне не происходит переноса энергии. Энергия просто переходит из потенциальной (при максимальном смещении точек среды от положения равновесия) в кинетическую (при прохождении точками положения равновесия)в пределах между узлами, остающимися неподвижными.
 Все точки стоячей
волны в пределах между узлами колеблются
в одинаковой фазе, а по разные стороны
от узла – в противофазе.
Все точки стоячей
волны в пределах между узлами колеблются
в одинаковой фазе, а по разные стороны
от узла – в противофазе.
Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.
Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.
Примеры решения задач
Пример . Определите скорость распространения звука в воде, если длина волны равна 2м, а частота колебаний источника ν=725Гц. Определите также наименьшее расстояние между точками среды, колеблющимися в одинаковой фазе.
Дано : λ=2м; ν=725Гц.
Найти : υ; х.
Решение . Длина волны равна расстоянию, на которое распространяется определённая фаза волны за период Т, т.е.
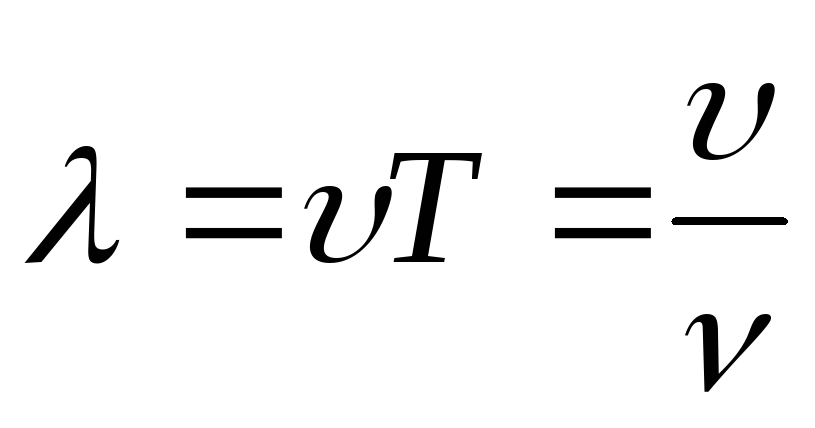 ,
,
где υ – скорость волны; ν - частота колебаний.
Тогда искомая скорость
Длина волны – расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе. Следовательно, искомое наименьшее расстояние между точками среды, колеблющимися в одинаковой фазы, равно длине волны, т.е.
Ответ: υ=1450 м/с; х=2м.
Пример . Определите, во сколько раз изменится длина ультразвуковой волны при переходе её из меди в сталь, если скорость распространения ультразвука в меди и стали соответственно равны υ 1 =3,6км/с и υ 2 =5,5 км/с.
Дано : υ 1 =3,6км/с=3,6∙10 3 м/с. и υ 2 =5,5 км/с =5,5∙10 3 м/с.
Найти
: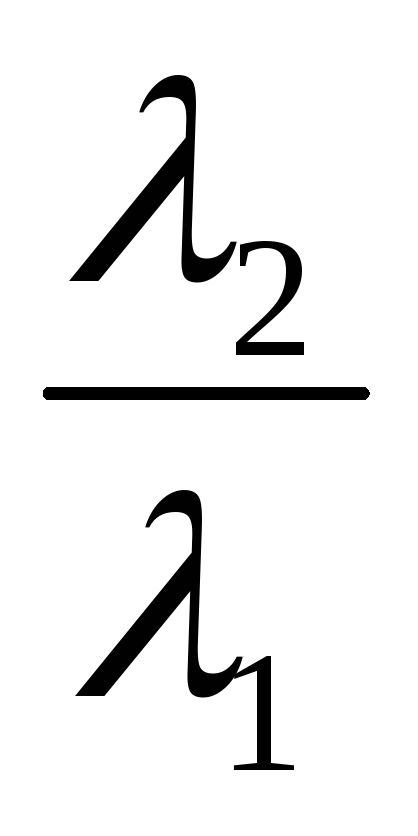 .
.
Решение . При распространении волн частота колебаний не изменяется при переходе их одной среды в другую (она зависит только от свойств источника волн), т.е. ν 1 = ν 2 = ν.
Связь длины волны с частотой ν:
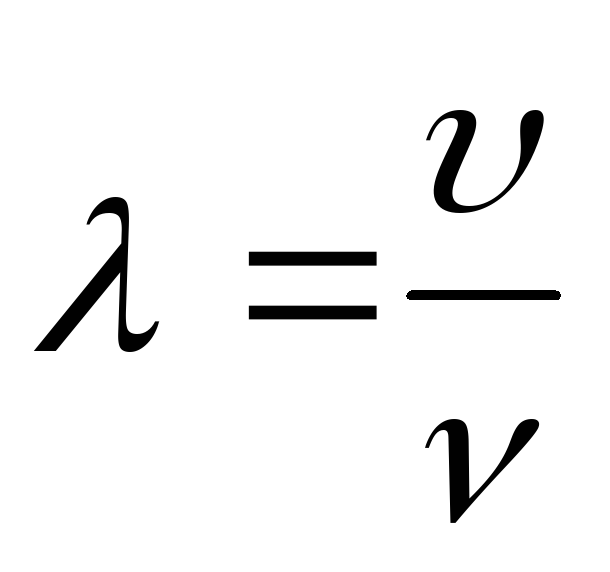 ,
(1)
,
(1)
где υ – скорость волны.
Искомое отношение, согласно (1),
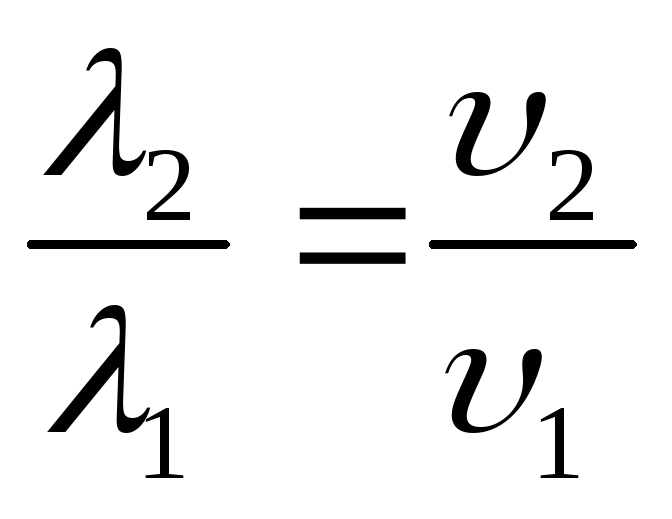 .
.
Вычисляя,
получаем
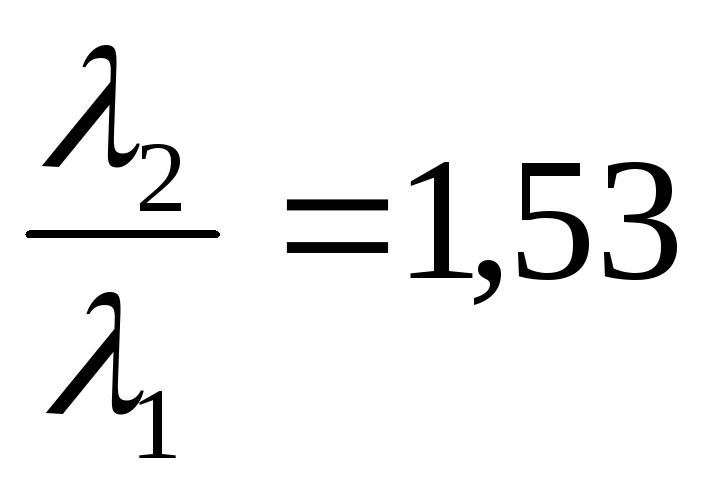 (увеличится в 1.53 раза).
(увеличится в 1.53 раза).
Ответ
:
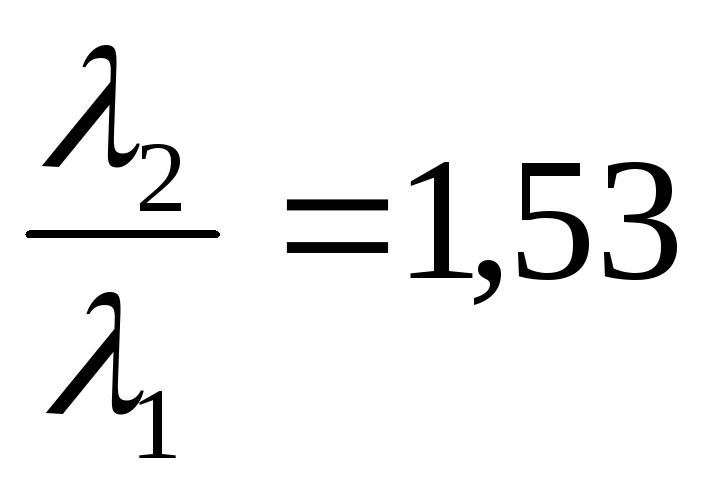
Пример
.
Один
конец упругого стержня соединён с
источником гармонических колебаний,
подчиняющихся закону
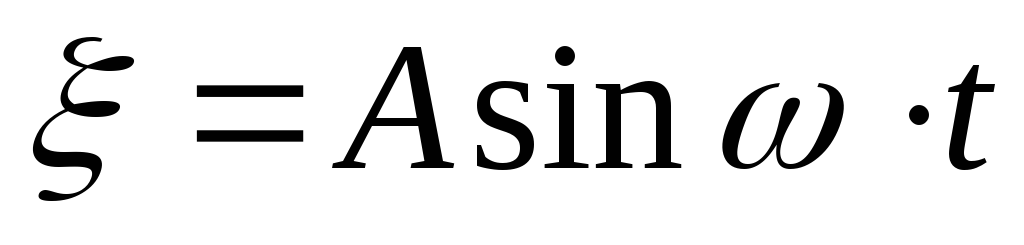 ,
а другой конец жёстко закреплён. Учитывая,
то отражение в месте закрепления стержня
происходит от более плотной среды,
определите: 1) уравнение стоячей волны;
2) координаты узлов; 3) координаты
пучностей.
,
а другой конец жёстко закреплён. Учитывая,
то отражение в месте закрепления стержня
происходит от более плотной среды,
определите: 1) уравнение стоячей волны;
2) координаты узлов; 3) координаты
пучностей.
Дано
:
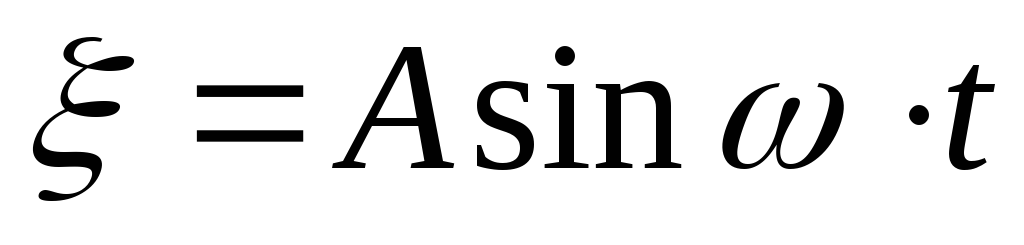 .
.
Найти : 1) ξ (x, t); 2) х у; 3) х n .
Решение . Уравнение падающей волны
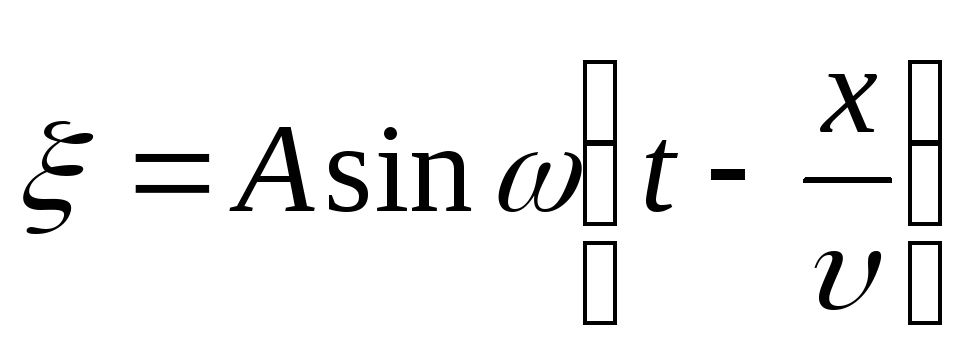 ,
(1)
,
(1)
где А – амплитуда волны; ω - циклическая частота; υ - скорость волны.
Согласно условию задачи, отражение в месте закрепления стержня происходит от более плотной среды, поэтому волна меняет фазу на противоположную, и уравнение отражённой волны
Сложив уравнения (1) и (2), получим уравнение стоячей волны
(учли
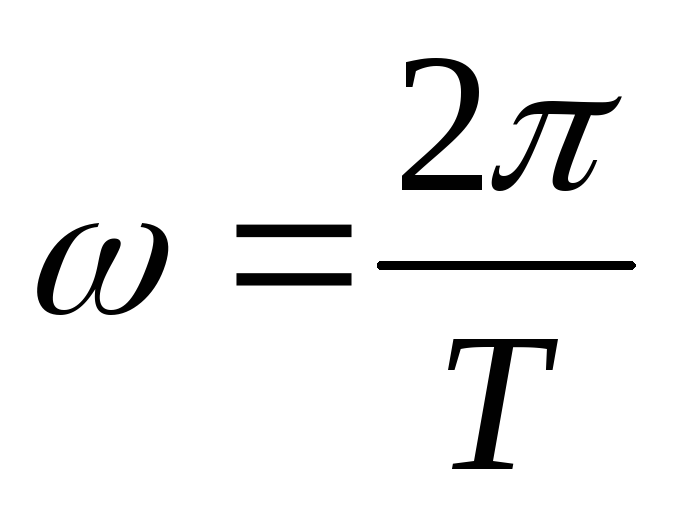 ;
λ=υТ).
;
λ=υТ).
В точках среды, где
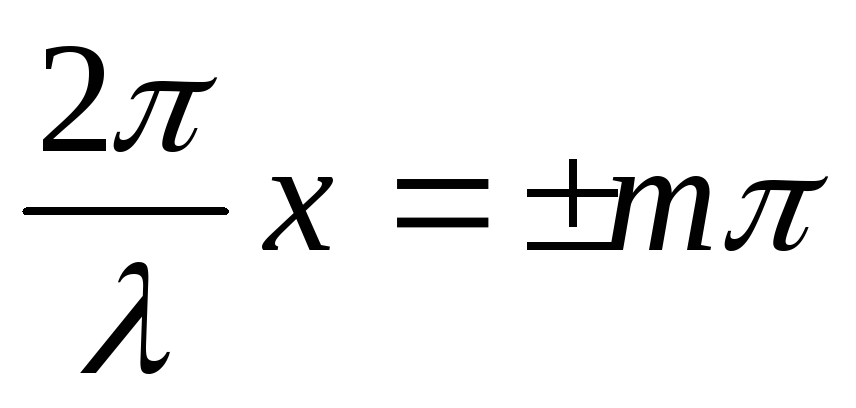 (m=0,
1, 2,….) (3)
(m=0,
1, 2,….) (3)
Амплитуда колебаний обращается в нуль (наблюдаются узлы), в точках среды, где
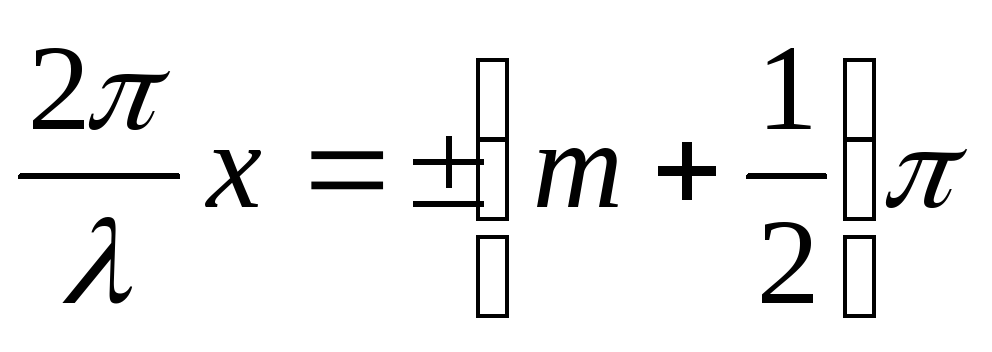 (m=0,
1, 2,….) (4)
(m=0,
1, 2,….) (4)
Амплитуда колебаний достигает максимального значения, равного 2А (наблюдаются пучности). Искомые координаты узлов и пучностей находим из выражений (3) и (4):
координаты
узлов
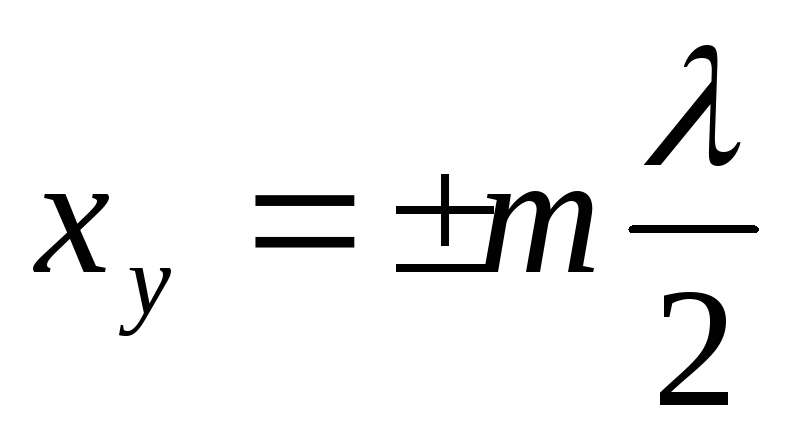 (m=0,
1, 2,….);
(m=0,
1, 2,….);
координаты
пучностей
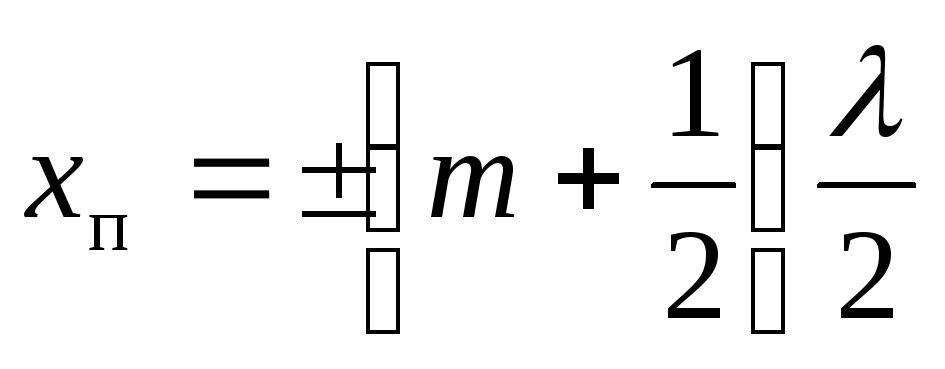 (m=0,
1, 2,….).
(m=0,
1, 2,….).
Ответ
:
1)
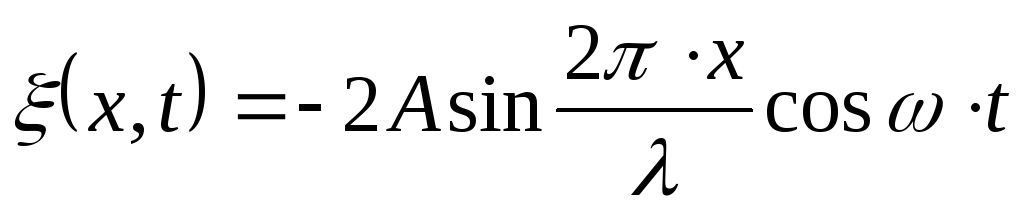 ;
;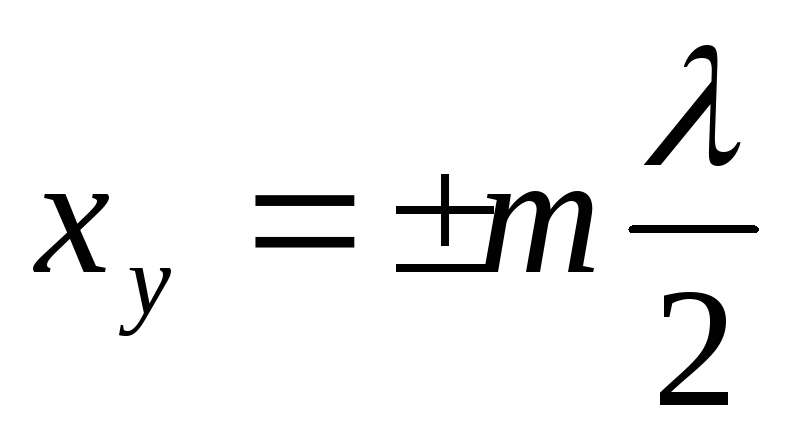 (m=0,
1, 2,….);
(m=0,
1, 2,….);
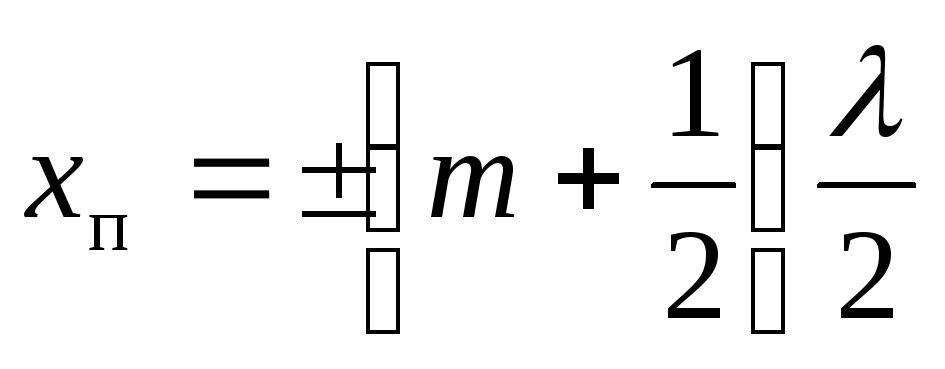 (m=0,
1, 2,….).
(m=0,
1, 2,….).
Пример . Расстояние между соседними узлами стоячей волны, создаваемый камертоном в воздухе ℓ =42см. Принимая скорость звука в воздухе υ=332 м/с, определите частоту колебаний ν камертона.
Дано : ℓ =42см=0,42м; υ=332 м/с.
Найти : ν.
Решение
.
В стоячеё волне расстояние между двумя
соседними узлами равно
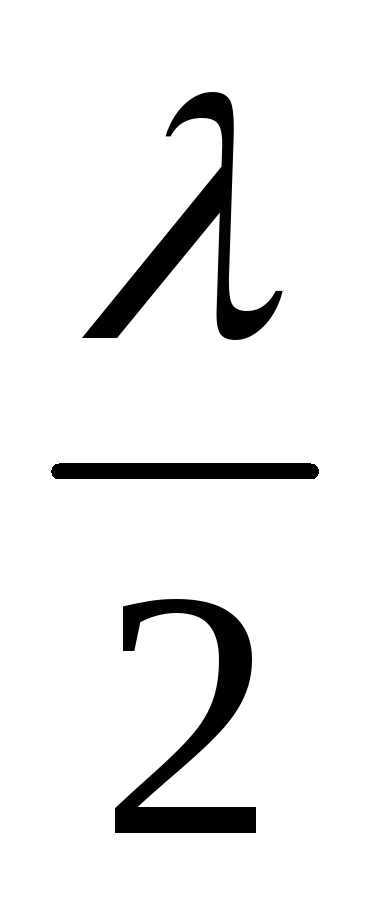 .
Следовательно, ℓ=
.
Следовательно, ℓ=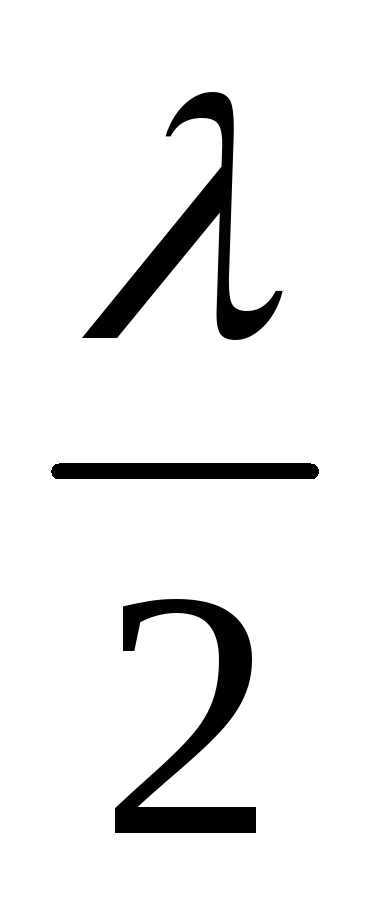 , откуда длина бегущей волны
, откуда длина бегущей волны
Связь
между длиной волны и частотой
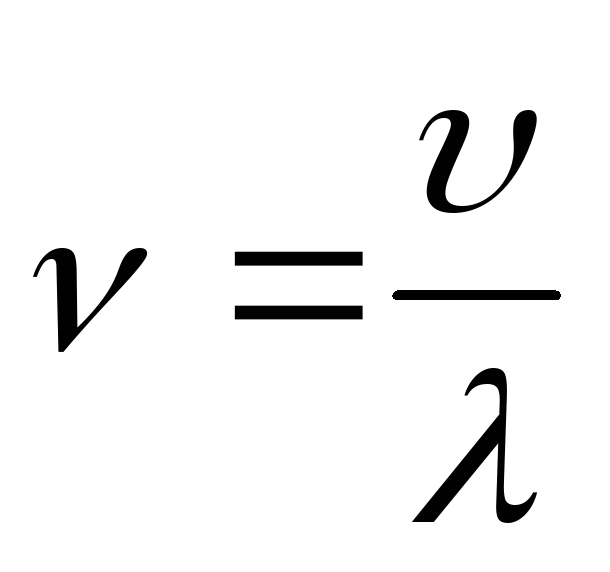 .
Подставив в эту формулу значение (1),
получим искомую частоту колебаний
камертона
.
Подставив в эту формулу значение (1),
получим искомую частоту колебаний
камертона
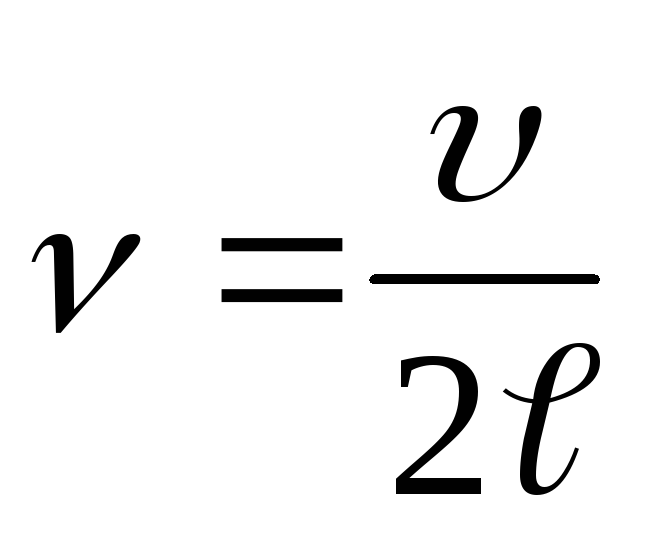 .
.
Ответ : ν=395 Гц.
Пример . Труба длиной ℓ = 50см заполнена воздухом и открыта с одного конца. Принимая скорость υ звука равной 340 м/с, определите, при какой наименьшей частоте в трубе будет возникать стоячая звуковая волна. Принимая скорость звука в воздухе υ=332 м/с, определите частоту колебаний ν камертона.
Дано : ℓ =50см=0,5м; υ=340 м/с.
Найти : ν 0 .
Решение. Частота будет минимальной при условии, что длина стоячей волны максимальна.
В открытой с одного конца трубе на открытой части будет пучность (отражение от менее плотной среды), а на закрытой части – узел (отражение от более плотной среды). Поэтому в трубе уложится четверть длины волны:
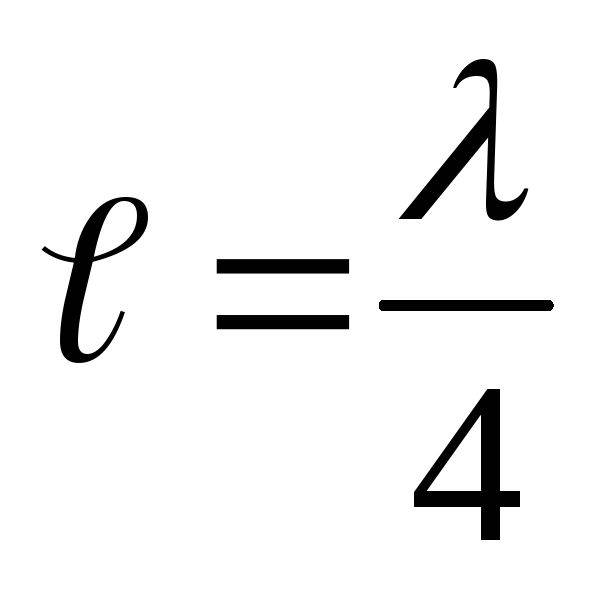
Учитывая,
что длина волны
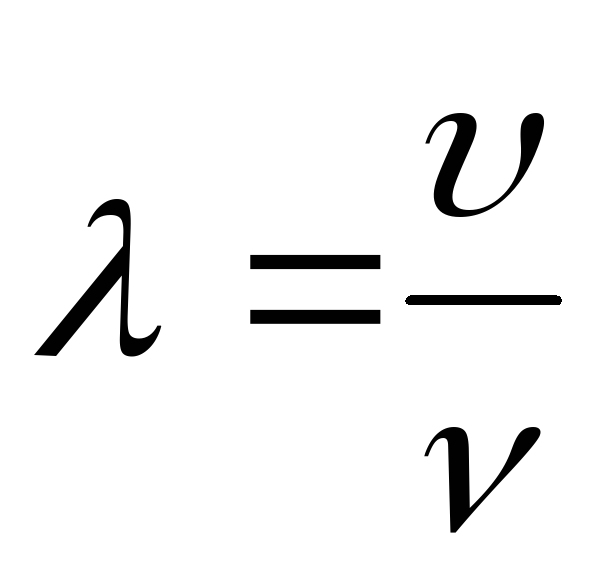 ,
можем записать
,
можем записать
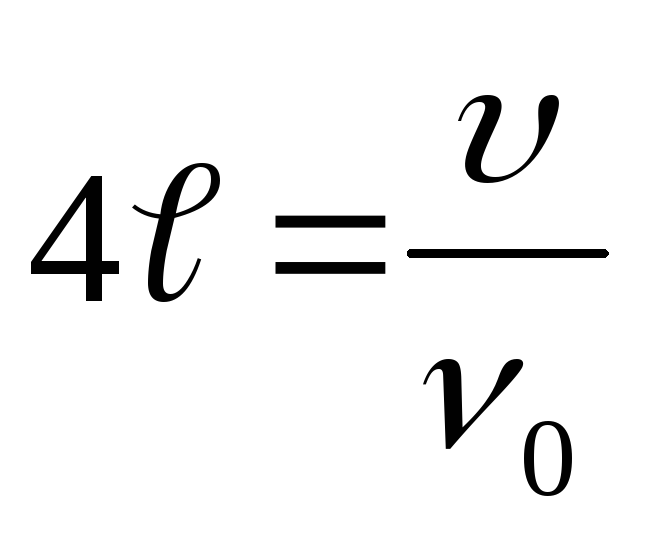 ,
,
Откуда искомая наименьшая частота
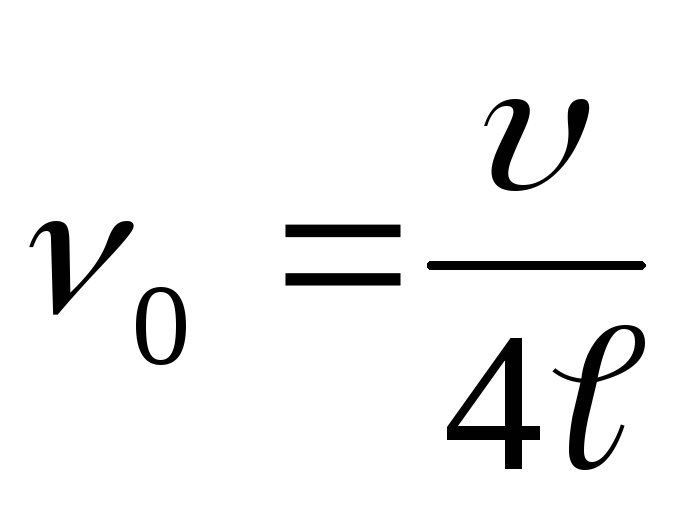 .
.
Ответ : ν 0 =170 Гц.
Пример . Два электропоезда движутся навстречу друг другу со скоростями υ 1 =20 м/с и υ 2 =10 м/с. Первый поезд даёт свисток, высота тона которого соответствует частоте ν 0 =600 Гц. Определите частоту, воспринимаемую пассажиром второго перед встречей поездов и после их встречи. Скорость звука принять равной υ=332 м/с.
Дано : υ 1 =20 м/с; υ 2 =10 м/с; ν 0 =600 Гц; υ=332 м/с.
Найти: ν ; ν".
Решение. Согласно общей формуле, описывающей эффект Доплера в акустике, частота звука, воспринимаемая движущимся приёмником,
![]() ,
(1)
,
(1)
где ν 0 - частота звука, посылаемая источником; υ пр - скорость движения приёмника; υ ист - скорость движения источника. Если источник и приёмник приближаются друг к другу, то берётся верхний знак, если удаляются – нижний знак.
Согласно обозначениями, данным в задаче (υ пр =υ 2 и υ ист =υ 1) и приведённым выше пояснениями, из формулы (1) искомые частоты, воспринимаемые пассажиром второго поезда:
Перед встречей поездов (электропоезда сближаются):
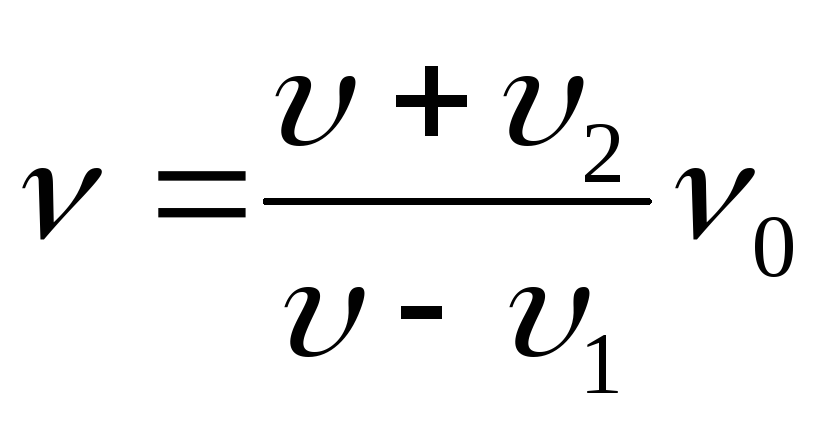 ;
;
После встречи поездов (поезда удаляются друг от друга):
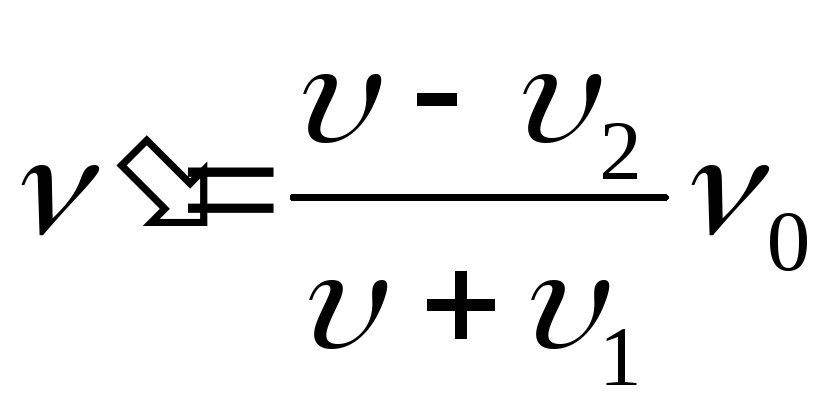
Ответ: ν=658 Гц; ν" =549 Гц.
Лекция № 14
Очень важный случай интерференции наблюдается при наложении плоских волн с одинаковой амплитудой. Возникающий в результате этого колебательный процесс принято называть стоячей волной .
Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.
Рассмотрим результат интерференции двух синусоидальных плоских волн одинаковой амплитуды, распространяющихся в противоположных направлениях.
Для простоты рассуждений допустим, что обе волны вызывают в начале координат колебания в одинаковой фазе. Уравнения этих колебаний имеют вид:
![]() ;
;
![]() .
.
Складывая оба уравнения и преобразовывая результат, по формуле для суммы синусов получим:
![]() - уравнение стоячей волны
.
- уравнение стоячей волны
.
Сравнивая это уравнение с уравнением гармонических колебаний, мы видим, что амплитуда результирующих колебаний равна
![]() .
.
Так как , а , то . Тогда
![]() .
.
В точках среды, где , колебания отсутствуют, ᴛ.ᴇ. . Эти точки называются узлами стоячей волны .
В точках, где , амплитуда колебаний имеет наибольшее значение, равное . Эти точки называются пучностями стоячей волны . Координаты пучностей находятся из условия , т.к. , то .
Аналогично координаты узлов находятся из условия
![]() .
.
![]() .
.
Из формул координат узлов и пучностей следует, что расстояние между соседними пучностями, также как и расстояния между соседними узлами, равно . Пучности и узлы сдвинуты друг относительно друга на четверть длины волны.
Сравним характер колебаний в стоячей и бегущей волне. В бегущей волне каждая точка совершает колебания, амплитуда которых не отличается от амплитуды других точек. Но колебания различных точек происходят с различными фазами .
В стоячей волне все частицы среды, находящиеся между двумя соседними узлами колеблются в одной и той же фазе, но с разными амплитудами. При переходе через узел фаза колебаний скачкообразно изменяется на , т.к. изменяется знак .
Графически стоячая волна должна быть изображена следующим образом:
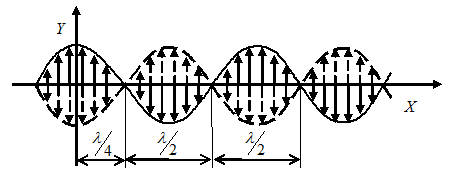 В момент времени, когда , все точки среды имеют макси-мальные смещения, на-правление которых опре-деляется знаком . Эти смещения показаны на рисунке сплошными стрелками.
В момент времени, когда , все точки среды имеют макси-мальные смещения, на-правление которых опре-деляется знаком . Эти смещения показаны на рисунке сплошными стрелками.
Спустя четверть периода, когда , смещения всех точек равны нулю. Частицы проходят через линию с различными скоростями.
Спустя еще четверть периода, когда , частицы опять будут иметь максимальные смещения, но противоположного направления (пунктирные стрелки).
При описании колебательных процессов в упругих системах за колеблющуюся величину можно принять не только смещение, но и скорость частиц, а также и величину относительной деформации среды.
Стоит сказать, что для нахождения закона изменения скорости стоячей волны продифференцируем по уравнение смещения стоячей волны и для нахождения закона изменения деформации продифференцируем по уравнение стоячей волны.
![]()
![]() .
.
Анализируя эти уравнения, мы видим, что узлы и пучности скорости совпадают с узлами и пучностями смещения; узлы и пучности деформации совпадают соответственно с пучностями и узлами скорости и смещения.
Колебания струны
В закрепленной с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причем в местах закрепления струны должны располагаться узлы. По этой причине в струне возбуждаются только такие колебания, половина длины которых укладывается на длине струны целое число раз.
Отсюда вытекает условие
где - длина струны.
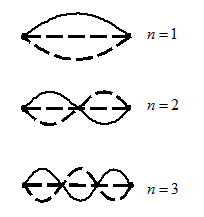 Или иначе . Этим длинам волн соответствуют частоты
Или иначе . Этим длинам волн соответствуют частоты ![]() , где - фазовая скорость волны. Величина ее определяется силой натяжения струны и ее массой.
, где - фазовая скорость волны. Величина ее определяется силой натяжения струны и ее массой.
При - основная частота.
При - собственные частоты колебаний струны или обертоны .
Эффект Допплера
Пусть в упругой среде на некотором расстоянии от источника колебаний располагается приемник колебаний. Когда источник колебаний и приемник неподвижны относительно среды, то частота колебаний, воспринимаемых приемником, будет равна частоте колебаний источника. В случае если же источник колебаний или приемник, или оба одновременно, движутся относительно среды, то частота колебаний, воспринимаемых приемником, может оказаться отличной от частоты колебаний источника. Это явление принято называть эффектом Допплера .
Рассмотрим простейшие случаи, когда источник волн и наблюдатель движутся относительно среды вдоль одной прямой:
1. Источник звука движется относительно среды со скоростью , приемник звука покоится.
![]() В этом случае за период колебаний звуковая волна отойдет от источ-ника на расстояние , а сам источник сместится на расстояние рав-ное .
В этом случае за период колебаний звуковая волна отойдет от источ-ника на расстояние , а сам источник сместится на расстояние рав-ное .
В случае если источник удалять от приемника, ᴛ.ᴇ. двигать в направлении обратном направлению распространения волны, то длина волны .
В случае если источник звука приближать к приемнику, ᴛ.ᴇ. двигать в направлении распространения волны, то .
Частота звука воспринимаемая приемником равна
Подставим вместо их значения для обоих случаев:
С учетом того, что , где - частота колебаний источника, равенство примет вид:
Разделим и числитель и знаменатель этой дроби на , тогда
2. Источник звука неподвижен, а приемник движется относительно среды со скоростью .
В этом случае длина волны в среде не изменяется и по-прежнему равна . Вместе с тем две последовательные амплитуды, отличающиеся по времени на один период колебаний , дойдя до движущегося приемника, будут отличаться по времени в моменты встречи волны с приемником на отрезок времени , величина которого больше или меньше в зависимости от того, удаляется или приближается приемник к источнику звука. За время звук распространяется на расстояние , а приемник сместится на расстояние . Сумма этих величин и дает нам длину волны :
Период колебаний, воспринимаемых приемником , связан с частотой этих колебаний соотношением
Подставив вместо его выражение из равенства (1), поучим
![]() .
.
Т.к. , где - частота колебаний источника, а , то
3. Источник и приемник звука движутся относительно среды. Соединяя результаты, полученные в двух предыдущих случаях, получим
Звуковые волны
В случае если упругие волны, распространяющиеся в воздухе, имеют частоту в пределах от 20 до 20000 Гц, то, достигнув человеческого уха, они вызывают ощущение звука. По этой причине волны лежащие в данном диапазоне частот называются звуковыми. Упругие волны с частотой менее 20 Гц называются инфразвуком . Волны с частотой более 20000 Гц называются ультразвуком . Ультразвуки и инфразвуки человеческое ухо не слышит.
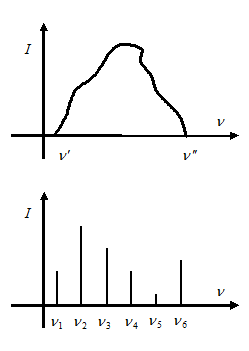 Звуковые ощущения характеризуются высотой звука, тембром и громкостью. Высота звука определяется частотой колебаний. При этом источник звука испускает не одну, а целый спектр частот. Набор частот колебаний, присутствующих в данном звуке, принято называть его акустическим спектром
. Энергия колебания распределяется между всеми частотами акустического спектра. Высота звука определяется по одной – основной частоте, в случае если на долю этой частоты приходится значительно большее количество энергии, чем на долю других частот.
Звуковые ощущения характеризуются высотой звука, тембром и громкостью. Высота звука определяется частотой колебаний. При этом источник звука испускает не одну, а целый спектр частот. Набор частот колебаний, присутствующих в данном звуке, принято называть его акустическим спектром
. Энергия колебания распределяется между всеми частотами акустического спектра. Высота звука определяется по одной – основной частоте, в случае если на долю этой частоты приходится значительно большее количество энергии, чем на долю других частот.
В случае если спектр состоит из множества частот, находящихся в интервале частот от до , то такой спектр принято называть сплошным (пример - шум).
В случае если спектр состоит из набора колебаний дискретных частот, то такой спектр принято называть линейчатым (пример – музыкальные звуки).
Акустический спектр звука исходя из своего характера и от распределения энергии между частотами определяет своеобразие звукового ощущения, называемое тембром звука. Различные музыкальные инструменты имеют различный акустический спектр, ᴛ.ᴇ. отличаются тембром звука.
Интенсивность звука характеризуется раз-личными величинами: колебаниями частиц среды, их скоростями, силами давления, напряжениями в них и др.
Она характеризует амплитуду колебаний каждой из этих величин. При этом, поскольку эти величины взаимосвязаны, целесообразно ввести единую энергетическую характеристику. Такая характеристика для волн любого типа была предложена в 1877 году. Н.А. Умовым.
И носит название вектора Умова
Для звукового поля вектор Умова носит название силы звука.
Сила звука является физической характеристикой интенсивности звука. Мы оцениваем ее субъективно, как громкость звука. Человеческое ухо воспринимает звуки, сила которых превышает неĸᴏᴛᴏᴩᴏᴇ минимальное значение, различное для различных частот. Это значение принято называть порогом слышимости звука. Важно заметить, что для средних частот порядка Гц порог слышимости порядка .При очень большой силе звука порядка звук воспринимается кроме уха органами осязания, а в ушах вызывает болевое ощущение.
Значение интенсивности, при котором это происходит, принято называть порогом болевого ощущения . Порог болевого ощущения, также как и порог слышимости, зависит от частоты.
Человек обладает довольно сложным аппаратом для восприятия звуков. Звуковые колебания собираются ушной раковиной и через слуховой канал воздействуют на барабанную перепонку. Колебания ее передаются в небольшую полость, называемую улиткой. Внутри улитки расположено большое количество волокон, имеющих различную длину и натяжение и, следовательно, различные собственные частоты колебаний. При действии звука каждое из волокон резонирует на тот тон, частота которого совпадает с собственной частотой волокна. Набор резонансных частот в слуховом аппарате и определяет область воспринимаемых нами звуковых колебаний.
Субъективно оцениваемая нашим ухом громкость возрастает гораздо медленнее, чем интенсивность звуковых волн. В то время, как интенсивность возрастает в геометрической прогрессии – громкость возрастает в арифметической прогрессии. На этом основании уровень громкости определяется как логарифм отношения интенсивности данного звука к интенсивности, принятой за исходную
То после прохождения участка длиной , сила звука будет равна
где - коэффициент поглощения звука.
Величина коэффициента поглощения звука возрастает пропорционально квадрату частоты звука, в связи с этим низкие звуки распространяются дальше высоких.
В архитектурной акустике для больших помещений существенную роль играет реверберация или гулкость помещений. Звуки, испытывая многократные отражения от ограждающих поверхностей, воспринимаются слушателем в течении некоторого довольно большого промежутка времени. Это увеличивает силу доходящего до нас звука, однако, при чересчур длительной реверберации отдельные звуки накладываются друг на друга и речь перестает восприниматься членораздельно. По этой причине стены залов покрывают специальными звукопоглощающими материалами для уменьшения реверберации.
Источником звуковых колебаний может служить любое колеблющееся тело: язычок звонка, камертон, струна скрипки, столб воздуха в духовых инструментах и т.д. эти же тела могут служить и приемниками звука, когда они приходят в движение под действием колебаний окружающей среды.
Ультразвук
Чтобы получить направленную, ᴛ.ᴇ. близко к плоской, волну размеры излучателя должны быть во много раз больше длины волны. Звуковые волны в воздухе имеют длину до 15 м, в жидких и твердых телах длина волны еще больше. По этой причине построить излучатель, который создавал бы направленную волну подобной длины, практически не представляется возможным.
Ультразвуковые колебания имеют частоту свыше 20000 Гц, в связи с этим длина волны их очень мала. С уменьшением длины волны уменьшается также роль дифракции в процессе распространения волн. По этой причине ультразвуковые волны бывают получены в виде направленных пучков, подобных пучкам света.
Для возбуждения ультразвуковых волн используют два явления: обратный пьезоэлектрический эффект и магнитострикцию .
Обратный пьезоэлектрический эффект состоит в том, что пластинка некоторых кристаллов (сегнетовой соли, кварца, титаната бария и др.) под действием электрического поля слегка деформируется. Поместив ее между металлическими обкладками, на которые подается переменное напряжение, можно вызвать вынужденные колебания пластинки. Эти колебания передаются окружающей среде и порождают в ней ультразвуковую волну.
Магнитострикция состоит по сути в том, что ферромагнитные вещества (железо, никель, их сплавы и т.д.) под действием магнитного поля деформируются. По этой причине, поместив ферромагнитный стержень в переменное магнитное поле, можно возбудить механические колебания.
Высокие значения акустических скоростей и ускорений, а также хорошо разработанные методы изучения и приема ультразвуковых колебаний, позволили использовать их для решения многих технических задач. Перечислим некоторые из них.
В 1928 ᴦ. советский ученый С.Я.Соколов предложил использовать ультразвук для целей дефектоскопии, ᴛ.ᴇ. для обнаружения скрытых внутренних дефектов типа раковин, трещин, рыхлот, шлаковых включений и др.
Размещено на реф.рф
в металлических изделиях. В случае если размеры дефекта превышают длину волны ультразвука, то ультразвуковой импульс отражается от дефекта и возвращается обратно. Посылая в изделие ультразвуковые импульсы, и регистрируя отраженные эхосигналы, можно не только обнаруживать наличие дефектов в изделиях, но и судить о размерах и месте расположения этих дефектов. Сегодня данный метод широко используется в промышленности.
Направленные ультразвуковые пучки нашли широкое применение для целей локации, ᴛ.ᴇ. для обнаружения в воде предметов и определения расстояния до них. Впервые идея ультразвуковой локации была выказана выдающимся французским физиком П.Ланжевеном и разработана им во время первой мировой войны для обнаружения подводных лодок. Сегодня принципы гидролокации используются для обнаружения айсбергов, косяков рыбы и т.д. этими методами должна быть также определена глубина моря под днищем корабля (эхолот).
Ультразвуковые волны большой амплитуды широко применяются в настоящее время в технике для механической обработки твердых материалов, очистки мелких предметов (деталей часовых механизмов, трубопроводов и т.д.), помещенных в жидкость, обезгаживания и т.д.
Создавая при своем прохождении сильные пульсации давления в среде, ультразвуковые волны обуславливают целый ряд специфических явлений: измельчение (диспергирование) частиц, взвешенных в жидкости, образование эмульсий, ускорение процессов диффузии, активацию химических реакций, воздействие на биологические объекты и т.д.
Стоячие волны - понятие и виды. Классификация и особенности категории "Стоячие волны" 2014, 2015.



