Интерференция сообщение. Интерференция - что такое? Что такое интерференция и дифракция
Интерференция - одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков - все это проявление интерференции света.
Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И.Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 3.7.1). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 3.7.2).
Ньютон не смог с точки зрения корпускулярной теории объяснить, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов.
Такой опыт несложно повторить в домашних условиях.
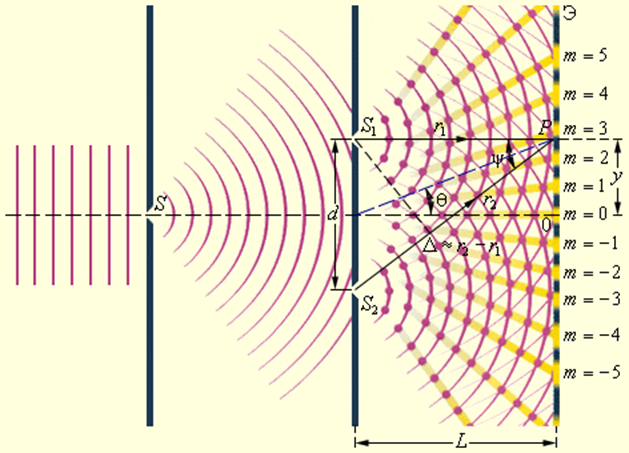
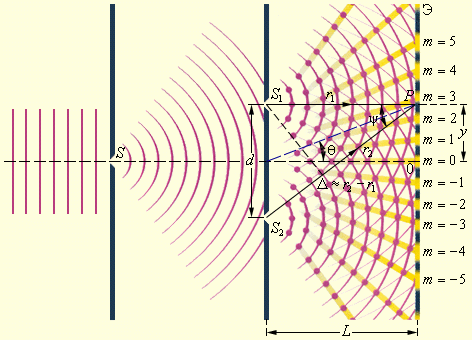
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S , падал на экран с двумя близко расположенными щелями S 1 и S 2 (рис. 3.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S 1 и S 2 , перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
|
|
|
Рисунок 3.7.3. Схема интерференционного опыта Юнга |
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S 1 и S 2 , которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S . При симметричном расположении щелей вторичные волны, испускаемые источниками S 1 и S 2 , находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r 1 и r 2 . Следовательно, фазы колебаний, создаваемых волнами от источников S 1 и S 2 в точке P , вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S 1 и S 2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции .
Монохроматическая (или синусоидальная) волна , распространяющаяся в направлении радиус-вектора , записывается в виде
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью : I = A 2 .
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P :
где Δ = r 2 - r 1 - так называемая разность хода .
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = m λ (m = 0, ±1, ±2, ...). При этом I max = (a 1 + a 2) 2 > I 1 + I 2 . Интерференционный минимум (темная полоса) достигается при Δ = m λ + λ / 2. Минимальное значение интенсивности I min = (a 1 - a 2) 2 < I 1 + I 2 . На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
В частности, если I 1 = I 2 = I 0 , т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
|
I = 2I 0 (1 + cos k Δ). |
В этом случае I max = 4I 0 , I min = 0.
Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.
Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:
![]()
При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl , т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,
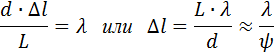
где ψ - угол схождения «лучей» в точке наблюдения P . Выполним количественную оценку. Допустим, что расстояние d между щелями S 1 и S 2 равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 10 5 нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика.
Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек.
В эксперименте Ньютона (рис. 3.7.1) при нормальном падении волны на плоскую поверхность линзы разность хода приблизительно равна удвоенной толщине 2h воздушного промежутка между линзой и плоскостью. Для случая, когда радиус кривизны R линзы велик по сравнению с h , можно приближенно получить:
где r - смещение от оси симметрии. При написании выражения для разности хода следует также учесть, что волны 1 и 2 отражаются при разных условиях. Первая волна отражается от границы стекло-воздух, а вторая - от границы воздух-стекло. Во втором случае происходит изменение фазы колебаний отраженной волны на π, что эквивалентно увеличению разности хода на λ / 2. Поэтому
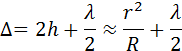
При r = 0, то есть в центре (точка соприкосновения) Δ = λ / 2; поэтому в центре колец Ньютона всегда наблюдается интерференционный минимум - темное пятно. Радиусы r m последующих темных колец определяются выражением
![]()
Эта формула позволяет экспериментально определить длину волны света λ, если известен радиус кривизны R линзы.
Проблема когерентности волн . Теория Юнга позволила объяснить интерференционные явления, возникающие при сложении двух монохроматических волн одной и той же частоты. Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), в каких - интенсивности волн, т. е. квадраты напряженностей полей? Теория интерференции монохроматических волн не может дать ответа на этот вопрос.
Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический (или случайный) характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10 -8 с). Результирующее излучение источника в каждый момент времени состоит из вкладов огромного числа атомов. Через время порядка τ вся совокупность излучающих атомов обновляется. Поэтому суммарное излучение будет иметь другую амплитуду и, что особенно важно, другую фазу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ. Отдельные «обрывки» излучения длительности τ называются цугами . Цуги имеют пространственную длину, равную c τ, где c - скорость света. Колебания в разных цугах не согласованы между собой. Таким образом, реальная световая волна представляет собой последовательность волновых цугов с беспорядочно меняющейся фазой . Принято говорить, что колебания в разных цугах некогерентны . Интервал времени τ, в течение которого фаза колебаний остается приблизительно постоянной, называют временем когерентности .
Интерференция может возникнуть только при сложении когерентных колебаний, т. е. колебаний, относящихся к одному и тому же цугу. Хотя фазы каждого из этих колебаний также подвержены случайным изменениям во времени, но эти изменения одинаковы, поэтому разность фаз когерентных колебаний остается постоянной. В этом случае наблюдается устойчивая интерференционная картина и, следовательно, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз оказывается случайной функцией времени. Интерференционные полосы испытывают беспорядочные перемещения из стороны в сторону, и за время Δt их регистрации, которая в оптических экспериментах значительно больше времени когерентности (Δt >> τ), происходит полное усреднение. Регистрирующее устройство (глаз, фотопластинка, фотоэлемент) зафиксирует в точке наблюдения усредненное значение интенсивности, равное сумме интенсивностей I 1 + I 2 обоих колебаний. В этом случае выполняется закон сложения интенсивностей.
Таким образом, интерференция может возникнуть только при сложении когерентных колебаний. Волны, создающие в точке наблюдения когерентные колебания, также называются когерентными. Волны от двух независимых источников некогерентны и не могут дать интерференции. Т. Юнг интуитивно угадал, что для получения интерференции света нужно волну от источника разделить на две когерентные волны и затем наблюдать на экране результат их сложения. Так делается во всех интерференционных схемах. Однако, даже в этом случае интерференционная картина исчезает, если разность хода Δ превысит длину когерентности c τ.
Знаете ли Вы,
что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, "мысленный эксперимент" фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей "мысленных экспериментов" является обман слушателя или читателя путем замены настоящего физического эксперимента его "куклой" - фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, "мысленными экспериментами" привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие "фантики" от настоящих ценностей.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Опыт Юнга является первым интерференционным опытом, получившим объяснение на основе волновой теории. В опыте Юнга свет от источника проходит через две близко расположенные щели. Световые пучки, расширяясь из-за дифракции, падают на удаленный экран. В области перекрытия световых пучков возникают интерференционные полосы.
Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.
Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рисунок 6). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рисунок 7).
Ньютон не смог с точки зрения корпускулярной теории объяснить, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов.
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S , падал на экран с двумя близко расположенными щелями S 1 и S 2 (рисунок 8). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S 1 и S 2 , перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
|
|
|
Рисунок 8 Схема интерференционного опыта Юнга |
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S 1 и S 2 , которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S . При симметричном расположении щелей вторичные волны, испускаемые источниками S 1 и S 2 , находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r 1 и r 2 . Следовательно, фазы колебаний, создаваемых волнами от источников S 1 и S 2 в точке P , вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S 1 и S 2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции .
Монохроматическая (или синусоидальная) волна , распространяющаяся в направлении радиус-вектора , записывается в виде
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью : I = A 2 .
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P :
|
|
где Δ = r 2 – r 1 – так называемая разность хода .
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = m λ (m = 0, ±1, ±2, ...). При этом I max = (a 1 + a 2) 2 > I 1 + I 2 . Интерференционный минимум (темная полоса) достигается при Δ = m λ + λ / 2. Минимальное значение интенсивности I min = (a 1 – a 2) 2 < I 1 + I 2 . На рисунке 9 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
В частности, если I 1 = I 2 = I 0 , т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
|
При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl , т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,
где ψ – угол схождения «лучей» в точке наблюдения P . Выполним количественную оценку. Допустим, что расстояние d между щелями S 1 и S 2 равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 10 5 нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика. Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек. В эксперименте Ньютона (рисунок 6) при нормальном падении волны на плоскую поверхность линзы разность хода приблизительно равна удвоенной толщине 2h воздушного промежутка между линзой и плоскостью. Для случая, когда радиус кривизны R линзы велик по сравнению с h, можно приближенно получить:
где r – смещение от оси симметрии. При написании выражения для разности хода следует также учесть, что волны 1 и 2 отражаются при разных условиях. Первая волна отражается от границы стекло–воздух, а вторая – от границы воздух–стекло. Во втором случае происходит изменение фазы колебаний отраженной волны на π, что эквивалентно увеличению разности хода на λ / 2. Поэтому
При r = 0, то есть в центре (точка соприкосновения) Δ = λ / 2; поэтому в центре колец Ньютона всегда наблюдается интерференционный минимум – темное пятно. Радиусы r m последующих темных колец определяются выражением
Эта формула позволяет экспериментально определить длину волны света λ, если известен радиус кривизны R линзы. Проблема когерентности волн. Теория Юнга позволила объяснить интерференционные явления, возникающие при сложении двух монохроматических волн одной и той же частоты. Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), в каких – интенсивности волн, т. е. квадраты напряженностей полей? Теория интерференции монохроматических волн не может дать ответа на этот вопрос. Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический (или случайный) характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10 –8 с). Результирующее излучение источника в каждый момент времени состоит из вкладов огромного числа атомов. Через время порядка τ вся совокупность излучающих атомов обновляется. Поэтому суммарное излучение будет иметь другую амплитуду и, что особенно важно, другую фазу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ. Отдельные «обрывки» излучения длительности τ называются цугами . Цуги имеют пространственную длину, равную c τ, где c – скорость света. Колебания в разных цугах не согласованы между собой. Таким образом, реальная световая волна представляет собой последовательность волновых цугов с беспорядочно меняющейся фазой . Принято говорить, что колебания в разных цугах некогерентны . Интервал времени τ, в течение которого фаза колебаний остается приблизительно постоянной, называют временем когерентности . Интерференция может возникнуть только при сложении когерентных колебаний, т. е. колебаний, относящихся к одному и тому же цугу. Хотя фазы каждого из этих колебаний также подвержены случайным изменениям во времени, но эти изменения одинаковы, поэтому разность фаз когерентных колебаний остается постоянной. В этом случае наблюдается устойчивая интерференционная картина и, следовательно, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз оказывается случайной функцией времени. Интерференционные полосы испытывают беспорядочные перемещения из стороны в сторону, и за время Δt их регистрации, которая в оптических экспериментах значительно больше времени когерентности (Δt >> τ), происходит полное усреднение. Регистрирующее устройство (глаз, фотопластинка, фотоэлемент) зафиксирует в точке наблюдения усредненное значение интенсивности, равное сумме интенсивностей I 1 + I 2 обоих колебаний. В этом случае выполняется закон сложения интенсивностей. Таким образом, интерференция может возникнуть только при сложении когерентных колебаний. Для возникновения интерференции волн необходимо, чтобы волны имели одинаковую частоту и разность фаз колебаний полей в этих волнах оставалась постоянной во времени. В этом случае интерференционная картина не размывается со временем и не перемещается в пространстве. Волны, удовлетворяющие указанным условиям, называются когерентными. Самый простой способ получения когерентных волн – расщепление волны от какого-то монохроматического источника на две или несколько волн (эти волны будут когерентны, если при расщеплении, например, при отражении от зеркала, не вносится неконтролируемая разность фаз). Затем можно разными способами заставить каждую из волн пройти разный путь. Это можно сделать, либо заставив два луча пройти разные расстояния в пространстве (как в опыте Юнга), либо заставив лучи пройти одно и то же расстояние, но в средах с разным показателем преломления, изменив тем самым скорость света. В обоих случаях возникает определенная постоянная разность хода лучей, приводящая при совмещении этих лучей к интерференционной картине. Волны от двух независимых источников некогерентны и не могут дать интерференции. Т. Юнг интуитивно угадал, что для получения интерференции света нужно волну от источника разделить на две когерентные волны и затем наблюдать на экране результат их сложения. Так делается во всех интерференционных схемах. Однако, даже в этом случае интерференционная картина исчезает, если разность хода Δ превысит длину когерентности c τ. |
В этой статье рассматривается такое явление физики, как интерференция: что такое, когда возникает и как применяется. Также подробно рассказывается о смежном понятии волновой физики - дифракции.
Виды волн
Когда в книге или в разговоре возникает слово «волна», то, как правило, сразу представляется море: синий простор, безмерная даль, одна за другой на берег набегают соленые валы. Житель степей представит себе другой вид: безбрежный простор травы, она колышется под ласковым ветерком. Кто-то еще вспомнит волны, рассматривая складки тяжелой портьеры или трепетание флага в солнечный день. Математик подумает о синусоиде, любитель радио - об электромагнитных колебаниях. Все они имеют различную природу и относятся к разным видам. Но неоспоримо одно: волна - это состояние отклонения от равновесия, превращения какого-то «гладкого» закона в колебательный. Именно для них применимо такое явление, как интерференция. Что такое и как она возникает, рассмотрим чуть позже. Сначала разберёмся, какими бывают волны. Перечислим следующие виды:
- механические;
- химические;
- электромагнитные;
- гравитационные;
- спиновые;
- вероятностные.
С точки зрения физики, волны переносят энергию. Но случается, что перемещается и масса. Отвечая на вопрос о том, что такое интерференция в физике, следует отметить, что она характерна для волн абсолютно любой природы.
Признаки различия волн
Как ни странно, но единого определения волны не существует. Их виды настолько разнообразны, что только типов классификации более десятка. По каким же признакам различают волны?
- По способу распространения в среде (бегущие или стоячие).
- По характеру самой и солитоны отличны именно по этому признаку).
- По типу распределения в среде (продольные, поперечные).
- По степени линейности (линейные или нелинейные).
- По свойствам среды, в которой они распространяются (дискретные, непрерывные).
- По форме (плоские, сферические, спиральные).
- По особенностям физической среды распространения (механические, электромагнитные, гравитационные).
- По направлению колебания частиц среды (волны сжатия или сдвига).
- По времени, которое требуется на возбуждение среды (одиночные, монохроматические, волновой пакет).
И к любому типу этих возмущений среды применима интерференция. Что такое особенное содержится в этом понятии и почему именно это явление делает наш мир таким, какой он есть, расскажем после приведения характеристик волны.
Характеристики волны
Вне зависимости от типа и вида волн, у них всех есть общие характеристики. Вот список:
- Гребень - это своего рода максимум. Для волн сжатия это место наибольшей плотности среды. Представляет собой наибольшее положительное отклонение колебания от состояния равновесия.
- Ложбина (в некоторых случаях долина) - это обратное гребню понятие. Минимум, наибольшее отрицательное отклонение от состояния равновесия.
- Временная периодичность, или частота - это время, за которое волна пройдет от одного максимума к другому.
- Пространственная периодичность, или длина волны - это расстояние между соседними пиками.
- Амплитуда - это высота пиков. Именно данное определение понадобится, чтобы разобраться, что такое интерференция волн.
Мы очень подробно рассмотрели волну, ее характеристики и различные классификации, ибо понятие «интерференция» невозможно объяснить без четкого понимания такого явления, как возмущение среды. Напоминаем, что интерференция имеет смысл только для волн.
Взаимодействие волн

Теперь мы вплотную подошли к понятию «интерференция»: что такое, когда возникает и как ее определить. Все перечисленные выше виды, типы и характеристики волн относились к идеальному случаю. Это были описания «сферического коня в вакууме», то есть неких теоретических конструкций, невозможных в реальном мире. Но на практике все пространство вокруг пронизано различными волнами. Свет, звук, тепло, радио, химические процессы - это периодические колебания среды. И все эти волны взаимодействуют. Надо отметить одну особенность: чтобы они могли повлиять друг на друга, у них должны быть схожие характеристики.
Волны звука никоим образом не смогут интерферировать со светом, а радиоволны никак не взаимодействуют с ветром. Конечно, влияние все равно есть, но оно настолько мало, что его действие просто не учитывается. Другими словами, при объяснении, что такое интерференция света, предполагается, что один фотон влияет на другой при встрече. Итак, подробнее.
Интерференция

Для многих видов волн действует принцип суперпозиции: встречаясь в одной точке пространства, они взаимодействуют. Обмен энергией отображается на изменении амплитуды. Закон взаимодействия следующий: если встречаются в одной точке два максимума, то в конечной волне интенсивность максимума увеличивается вдвое; если встречаются максимум и минимум, то итоговая амплитуда обращается в ноль. Это и есть наглядный ответ на вопрос о том, что такое интерференция света и звука. По сути, это явление наложения.
Интерференция волн с разными характеристиками
Описанное выше событие представляет встречу двух одинаковых волн в линейном пространстве. Однако две встречные волны могут иметь разные частоты, амплитуды, длины. Как представить итоговую картину в таком случае? Ответ кроется в том, что результат будет не совсем похож на волну. То есть строгий порядок чередования максимумов и минимумов будет нарушен: в какой-то момент амплитуда будет максимальной, в следующий - уже меньше, потом встретятся максимум и минимум и результат обратится в ноль. Однако, какими бы сильными ни были различия двух волн, амплитуда все равно рано или поздно повторится. В математике принято говорить о бесконечности, но в реальности силы трения и инерция могут остановить само существование результирующей волны до того, как картина пиков, долин и равнин повторится.
Интерференция волн, встречающихся под углом

Но, помимо собственных характеристик, у реальных волн может различаться положение в пространстве. Например, при рассмотрении вопроса о том, что такое интерференция звука, это необходимо учитывать. Представьте: идет мальчик и дует в свистульку. Он посылает звуковую волну впереди себя. А мимо него проезжает другой мальчик на велосипеде и звенит в звонок, чтобы пешеход посторонился. В месте встречи этих двух звуковых волн они пересекаются под некоторым углом. Как рассчитать амплитуду и форму конечного колебания воздуха, который долетит, например, до ближайшей торговки семечками бабушки Маши? Тут в силу вступает векторная составляющая звуковой волны. И складывать или вычитать в данном случае надо не только величины амплитуды, но и векторы распространения этих колебаний. Надеемся, что бабушка Маша при этом не будет сильно кричать на шумящих ребят.
Интерференция света с разной поляризацией
Бывает и так, что в одной точке встречаются фотоны разной поляризации. В этом случае тоже следует учитывать векторную составляющую электромагнитных колебаний. Если они не взаимно перпендикулярны или один из пучков света имеет круговую или эллиптическую поляризацию, то взаимодействие вполне возможно. На этом принципе строится несколько способов определения оптической чистоты кристаллов: в перпендикулярно поляризованных пучках не должно быть никакого взаимодействия. Если картина искажается, то кристалл неидеален, он изменяет поляризацию пучков, а значит, выращен неправильно.
Интерференция и дифракция

Взаимодействие двух пучков света приводит к их интерференции, в итоге наблюдатель видит ряд светлых (максимумов) и темных (минимумов) полос или колец. А вот взаимодействие света и вещества сопровождается другим явлением - дифракцией. Оно основано на том, что свет разной длины волны иначе преломляется средой. Например, если длина волны 300 нанометров, то угол отклонения составляет 10 градусов, а если 500 нанометров - уже 12. Таким образом, когда на призму из кварца падает свет от солнечного луча, красный преломляется не так, как фиолетовый (их длины волн различаются), и наблюдатель видит радугу. Это ответ на вопрос о том, что такое интерференция и дифракция света и чем они отличаются. Если направить на ту же призму монохроматическое излучение от лазера, никакой радуги не будет, так как нет фотонов различной длины волны. Просто луч отклонится от первоначального направления распространения на некоторый угол, и все.
Применение явления интерференции на практике

Возможностей получить практическую пользу из этого сугубо теоретического явления очень много. Здесь будут перечислены лишь основные из них:
- Исследование качества кристаллов. Чуть выше мы рассказывали об этом.
- Выявление погрешностей линз. Часто они должны быть отшлифованы в идеальной сферической форме. Наличие каких-либо дефектов обнаруживают именно с помощью явления интерференции.
- Определение толщины пленок. В некоторых видах производства очень много значит постоянная толщина пленки, например пластиковой. Определить ее качество позволяет именно явление интерференции вместе с дифракцией.
- Просветление оптики. Очки, линзы фотоаппаратов и микроскопов покрывают тонкой пленкой. Таким образом, электромагнитные волны определенной длины просто отражаются и накладываются сами на себя, уменьшая помехи. Чаще всего просветление делается в зеленой части оптического спектра, так как именно эту область человеческий глаз воспринимает лучше всего.
- Изучение космоса. Зная законы интерференции, астрономы способны разделить спектры двух близко расположенных звезд и определить их составы и расстояние до Земли.
- Теоретические исследования. Когда-то именно с помощью явления интерференции удалось доказать волновую природу элементарных частиц, таких как электроны и протоны. Этим была подтверждена гипотеза корпускулярно-волнового дуализма микромира и положено начало квантовой эре.
Надеемся, что с данной статьёй ваши познания о наложении когерентных (испускаемых источниками, имеющими постоянную разность фаз и одинаковую частоту) волн значительно расширились. Это явление и называется интерференцией.

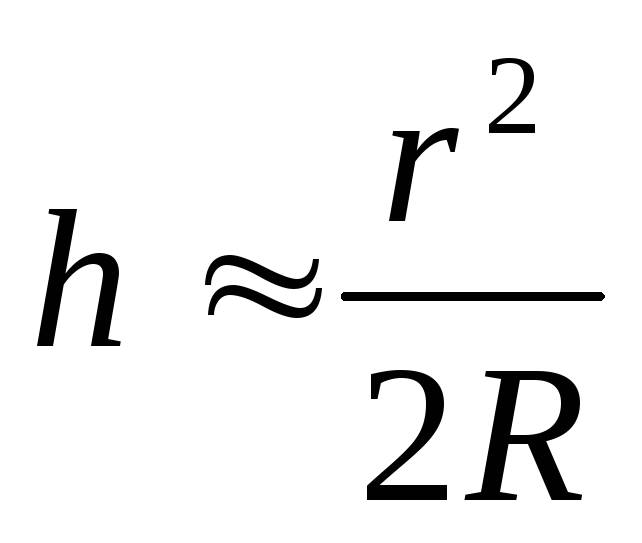 (6)
(6)
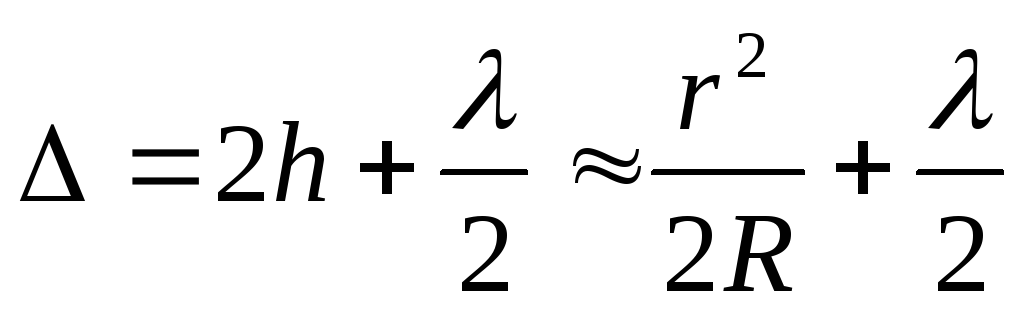 (7)
(7)
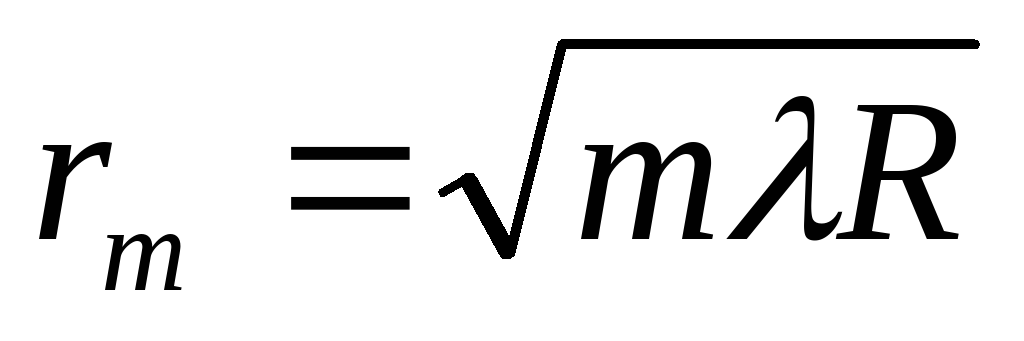 (8)
(8)


