Энергия конденсатора равна
Электроемкостью (емкостью) C уединенного изолированного проводника называется физическая величина, равная отношению изменения заряда проводника q к изменению его потенциала f: C = Dq/Df.
Электроемкость уединенного проводника зависит только от его формы и размеров, а также от окружающей его диэлектрической среды (e). Единица измерения емкости в системе СИ называется Фарадой. Фарада (Ф) - это емкость такого уединенного проводника, потенциал которого повышается на 1 Вольт при сообщении ему заряда в 1 Кулон. 1 Ф = 1 Кл/1 В.
Конденсатором называют систему двух разноименно заряженных проводников, разделенных диэлектриком (например, воздухом). Свойство конденсаторов накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется величиной, называемой электроемкостью конденсатора. Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U: C = Q/U.
В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.
Соединение конденсаторов в батареи. На практике конденсаторы часто соединяют в батареи - последовательно или параллельно.
При параллельном соединении напряжение на всех обкладках одинаковое U1 = U2 = U3 = U = e, а емкость батареи равняется сумме емкостей отдельных конденсаторов C = C1 + C2 + C3.
При последовательном соединении заряд на обкладках всех конденсаторов одинаков Q1 = Q2 = Q3, а напряжение батареи равняется сумме напряжений отдельных конденсаторов U = U1 + U2 + U3.
Емкость всей системы последовательно соединенных конденсаторов рассчитывается из соотношения: 1/C = U/Q = 1/C1 + 1/C2 + 1/C3.
Емкость батареи последовательно соединенных конденсаторов всегда меньше, чем емкость каждого из этих конденсаторов в отдельности. Энергия электростатического поля. Энергия заряженного плоского конденсатора Eк равна работе A, которая была затрачена при его зарядке, или совершается при его разрядке. A = CU2/2 = Q2/2С = QU/2 = Eк. Поскольку напряжение на конденсаторе может быть рассчитано из соотношения: U = E*d, где E - напряженность поля между обкладками конденсатора, d - расстояние между пластинами конденсатора, то энергия заряженного конденсатора равна: Eк = CU2/2 = ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2, где V - объем пространства между обкладками конденсатора. Энергия заряженного конденсатора сосредоточена в его электрическом поле.
|
Тип конденсатора |
Формула для расчета емкости |
Примечания |
Схематическое изображение |
|
Плоский конденсатор |
S - площадь пластины; d - расстояние между пластинами. | ||
|
Сферический конденсатор |
C = 4pee0R1R2/(R2 - R1) |
R2 и R1 - радиусы внешней и внутренней обкладок. | |
|
Цилиндрический конденсатор |
C = 2pee0h/ln(R2/R1) |
h - высота цилиндров. |
Как и любая система заряженных тел, конденсатор обладает энергией. Вычислить энергию заряженного плоского конденсатора с однородным полем внутри него несложно. Энергия заряженного конденсатора. Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта работа равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, содержащую лампу накаливания, рассчитанную на напряжение в несколько вольт (рис.14.37 ). При разрядке конденсатора лампа вспыхивает. Энергия конденсатора превращается в тепло и энергию света.
Выведем формулу для энергии плоского конденсатора. Напряженность поля, созданного зарядом одной из пластин, равна Е/2 , где Е -напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q , распределенный по поверхности другой пластины (рис.14.38 ). Согласно формуле (14.14) для потенциальной энергии заряда в однородном поле энергия конденсатора равна:
где q - заряд конденсатора, а d - расстояние между пластинами. Так как Ed=U , где U - разность потенциалов между обкладками конденсатора, то его энергия равна:
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную. Заменив в формуле (14.25) разность потенциалов или заряд с помощью выражения (14.22) для электроемкости конденсатора, получим:
W=qU/2=q^2/ 2C=CU^2/ 2
Можно доказать, что эти формулы справедливы для любого конденсатора, а не только для плоского. Энергия электрического поля. Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электрическом поле этих тел. Значит, энергия может быть выражена через основную характеристику поля - напряженность . Так как напряженность электрического поля прямо пропорциональна разности потенциалов (U=Ed , то согласно формуле W=qU/2=q^2/ 2C=CU^2/ 2
энергия конденсатора прямопропорциональна квадрату напряженности электрического поля внутри него: W~E^2. Применение конденсаторов . Зависимость электроемкости конденсатора от расстояния между его пластинами используется при создании одного из типов клавиатур компьютера. На тыльной стороне каждой клавиши располагается одна пластина конденсатора, а на плате, расположенной под клавишами, - другая. Нажатие клавиши изменяет емкость конденсатора. Электронная схема, подключенная к этому конденсатору, преобразует сигнал в соответствующий код, передаваемый в компьютер. Энергия конденсатора обычно не очень велика - не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, аккумуляторы в качестве источников электрической энергии. Но это совсем не означает, что конденсаторы как накопители энергии не получили практического применения. Они имеют одно важное свойство: конденсаторы могут накапливать энергию более или менее длительное время, а при разрядке через цепь с малым сопротивлением они отдают энергию почти мгновенно. Именно это свойство широко используют на практике. Лампа-вспышка, применяемая в фотографии , питается электрическим током разряда конденсатора, заряжаемого предварительно специальной батареей. Возбуждение квантовых источников света - лазеров осуществляется с помощью газоразрядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроемкости. Однако основное применение конденсаторы находят в радиотехнике. Энергия конденсатора пропорциональна его электроемкости и квадрату напряжения между пластинами. Вся эта энергия сосредоточена в электрическом поле. Энергия поля пропорциональна квадрату напряженности поля.
В заряженном конденсаторе обкладки име-ют разноименные заряды и взаимодейст-вуют между собой благодаря электричес-кому полю, которое сосредоточено в прост-ранстве между обкладками. О телах, между которыми существует взаимодействие, гово-рят, что они имеют потенциальную энер-гию. Следовательно, можно говорить и об энергии заряженного конденсатора .
Обкладки заряженного конден-сатора взаимодействуют между собой.
Наличие энергии у заряженного конден-сатора можно подтвердить опытами.
Возьмем конденсатор достаточно боль-шой емкости, источник тока, лампочку на-кала и составим электрическую цепь, схема которой изображена на рис. 4.82. Переведем переключатель S в положение 1 и зарядим конденсатор до определенной разности по-тенциалов от источника GB. Если после этого перевести переключатель в положение 2, то можно наблюдать кратковременную вспышку света вследствие накала нити лам-почки. Наблюдаемое явление можно объяс-нить тем, что заряженный конденсатор имел энергию , за счет которой была выполнена работа по накалу спирали лампочки.
В соответствии с законом сохранения энер-гии работа, выполненная при разрядке кон-денсатора, равняется работе, выполненной при его зарядке. Расчет этой работы и, соответственно, потенциальной энергии кон-денсатора осложнен особенностями процес-са зарядки конденсатора. Пластины его за-ряжаются и разряжаются постепенно. Зави-симость заряда Q конденсатора от времени при зарядке показана на графике (рис. 4.83). Заряд не только увеличивается постепенно, но и скорость его изменения не остается постоянной. Итак, вести расчеты на осно-вании формулы A = qEd нельзя, поскольку напряженность электрического поля не остается постоянной. Разность потенциалов также изменяется от нуля до максимально-го значения. На рис. 4.84 показано, что разность потенциалов изменяется про-порционально заряду конденсатора. Такая зависимость характерна для силы упругос-ти, которая зависит от удлинения пружины (рис. 4.85).
Воспользовавшись таким подобием, мож-но сделать вывод, что энергия заряженного конденсатора будет равна
W = Q Δφ / 2. Материал с сайта
Эта энергия равна работе по зарядке конденсатора, которая численно равна пло-щади заштрихованного треугольника на гра-фике рис. 4.84.
Учитывая, что Q = C Δφ , получим
W = C(Δφ) 2 / 2.
А если учесть связь разности потенциалов с зарядом Δφ = Q / C , то потенциальная энер-гия конденсатора может быть вычислена по формуле
W = (Q / 2) . (Q / C) = Q 2 / 2 C.
На этой странице материал по темам:
Энергия заряженного конденсатора шпора
Энергия заряженного конденсатора
Какие физические величины определяют энергию конденсатора
Самостоятельная работа по теме электроемкость плоского конденсатора
Як визначити енергію конденсатора за допомогою графіка
Вопросы по этому материалу:
Пусть потенциал обкладки конденсатора, на которой находится заряд равен а потенциал обкладки, на которой находится заряд , равен Тогда каждый из элементарных зарядов на которые можно разделить заряд находится в точке с потенциалом а каждый из зарядов, на которые можно разделить заряд , в точке с потенциалом .
Согласно формуле (28.1) энергия такой системы зарядов равна
Воспользовавшись соотношением (27.2), можно написать три выражения для энергии заряженного конденсатора:
![]()
Формулы (29.2) отличаются от формул (28.3) только заменой на
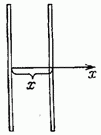
С помощью выражения для потенциальной энергии можно найти силу, с которой пластины плоского конденсатора притягивают друг друга. Допустим, что расстояние между пластинами может меняться. Свяжем начало оси х с левой пластиной (рис. 29.1). Тогда координата х второй пластины будет определять зазор d между обкладками. Согласно формулам (27.3) и (29.2)
![]()
Продифференцируем это выражение по х, полагая заряд на обкладках неизменным (конденсатор отключен от источника напряжения). В результате получим проекцию на ось х силы, действующей на правую пластину:
![]()
Модуль этого выражения дает величину силы, с которой обкладки притягивают друг друга:
Теперь попытаемся вычислить силу притяжения между обкладками плоского конденсатора как произведение напряженности поля, создаваемого одной из обкладок, на заряд, сосредоточенный на другой. Согласно формуле (14.3) напряженность поля, создаваемого одной обкладкой, равна
![]()
Диэлектрик ослабляет поле в зазоре в раз, но это имеет место только внутри диэлектрика (см. формулу (20.2) и связанный с нею текст). Заряды на обкладках располагаются вне диэлектрика и поэтому находятся под действием поля напряженности (29.4).
Умножив заряд обкладки q на эту напряженность, получим для силы выражение
Формулы (29.3) и (29.5) не совпадают. С опытом согласуется значение силы (29.3), получающееся из выражения для энергии. Это объясняется тем, что, кроме «электрической» силы (29.5), на обкладки действуют со стороны диэлектрика механические силы, стремящиеся их раздвинуть (см. § 22; отметим, что мы имеем в виду жидкий или газообразный диэлектрик). У края обкладок имеется рассеянное поле, убывающее по величине при удалении от краев (рис. 29.2). Молекулы диэлектрика, обладая дипольным моментом, испытывают дйствие силы, втягивающей их в область более сильного поля (см. формулу (9.16)). В результате давление между обкладками повышается и появляется сила, ослабляющая действие силы (29.5) в раз.
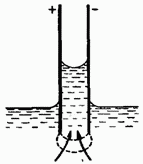
Если заряженный конденсатор с воздушным зазором частично погрузить в жидкий диэлектрик, наблюдается втягивание диэлектрика в пространство между пластинами (рис. 29.3). Это явление объясняется следующим образом. -Диэлектрическая проницаемость воздуха практически равна единице. Поэтому до погружения пластин в диэлектрик емкость конденсатора можно считать равной а энергию равной При частичном заполнении зазора диэлектриком конденсатор можно рассматривать как два параллельно включенных конденсатора, один из которых имеет площадь обкладки, равную - относительная часть зазора, заполненная жидкостью), и заполнен диэлектриком с второй с воздушным зазором имеет площадь обкладки, равную При параллельном включении конденсаторов емкости складываются:
Поскольку энергия будет меньше, чем (заряд q предполагается неизменным - перед погружением в жидкость конденсатор был отключен от источника напряжения). Следовательно, заполнение зазора диэлектриком оказывается энергетически выгодным. Поэтому диэлектрик втягивается в конденсатор и уровень его в зазоре поднимается. Это в свою очередь приводит к возрастанию потенциальной энергии диэлектрика в поле сил тяжести. В конечном итоге уровень диэлектрика в зазоре установится на некоторой высоте, соответствующей минимуму суммарной энергии (электрической и гравитационной). Рассмотренное явление сходно с капиллярным поднятием жидкости в узком зазоре между пластинками (см. § 119 1-го тома).
Втягивание диэлектрика в зазор между обкладками можно яснить также и с микроскопической точки зрения. У краев пластин конденсатора имеется неоднородное поле. Молекулы диэлектрика обладают собственным дипольным моментом либо приобретают его под действием поля; поэтому на них действуют силы, стремящиеся переместить их в область сильного поля, т. е. внутрь конденсатора. Под действием этих сил жидкость втягивается в зазор до тех пор, пока электрические силы, действующие на жидкость у края пластин, не будут уравновешены весом столба жидкости.



