Преломление луча из воздуха в стекло. Глава восьмая. отражение и преломление света
Световой пучок выходит из стекла в воздух (см. рисунок).
1) увеличивается;
2) уменьшается;
3) не изменяется.
Решение.
При переходе светового пучка из стекла в воздух частота электромагнитных колебаний в световой волне не изменяется, поскольку она не зависит от того, в какой среде распространяется волна. Так как стекло является оптически более плотной средой, чем воздух, при выходе из стекла скорость распространения световой волны увеличивается. В свою очередь, длина волны связана с частотой электромагнитных колебаний и скоростью распространения соотношением В виду неизменности частоты и увеличения скорости отсюда следует, что длина волны увеличивается.
Ответ: 311.
Ответ: 311
Световой пучок переходит из воздуха в стекло (см. рисунок).
Что происходит при этом с частотой электромагнитных колебаний в световой волне, скоростью их распространения, длиной волны?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение.
При переходе светового пучка из воздуха в стекло частота электромагнитных колебаний в световой волне не изменяется, поскольку она не зависит от того, в какой среде распространяется волна. Так как стекло является оптически более плотной средой, чем воздух, при переходе в стекло скорость распространения световой волны уменьшается. В свою очередь, длина волны связана с частотой электромагнитных колебаний и скоростью распространения соотношением В виду неизменности частоты и уменьшения скорости отсюда следует, что длина волны уменьшается.
Ответ: 322.
Ответ: 322
Предмет находится перед собирающей линзой между фокусным и двойным фокусным расстоянием. Как изменятся расстояние от линзы до его изображения, линейный размер изображения предмета и вид изображения (мнимое или действительное) при перемещении предмета на расстояние больше двойного фокусного ()?
| A | Б | В |
Решение.
Собирающая линза даёт действительное изображение предмета, если он удалён от линзы на расстояние, большее чем фокусное. Следовательно, при переносе предмета из положения между фокусным и двойным фокусным расстояниями на расстояние, большее двойного фокусного, вид изображения не изменится, он останется действительным (В — 3). Согласно формуле тонкой линзы, расстояние от предмета до линзы, расстояние от линзы до изображения и фокусное расстояние связаны соотношением Следовательно, в результате переноса расстояние от линзы до изображения уменьшится (А — 2).
Из рисунка видно, что линейные размеры предмета и изображения связаны с расстояниями от предмета и изображения до линзы соотношением Таким образом, при удалении предмета, линейный размер изображения будет уменьшаться (Б — 2).
Ответ: 223.
Ответ: 223
Небольшой предмет находится на главной оптической оси тонкой собирающей линзы, на двойном фокусном расстоянии от нее. Как изменятся при удалении предмета от линзы следующие три величины: размер изображения, его расстояние от линзы, оптическая сила линзы?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение.
В исходных условиях изображение предмета, даваемое линзой, - перевернутое, причем таких же размеров, что и оригинал. В соответствии с формулой тонкой линзы, чем дальше от линзы будет предмет при тех же исходных условиях, тем ближе к ней будет его изображение. Что же касается оптической силы линзы, то она, как и фокусное расстояние, является характеристикой линзы и не зависит от расположений предмета и его изображения.
Оптическая сила линзы (величина, обратная к фокусному расстоянию) является характеристикой самой линзы, поэтому при удалении предмета от линзы она никак не изменяется. Согласно формуле тонкой линзы расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние связаны соотношением
Следовательно при удалении предмета от линзы изображение будет приближаться к линзе. Из рисунка видно, что линейные размеры предмета и изображения связаны с расстояниями от предмета и изображения до линзы соотношением Таким образом, при удалении предмета, размер изображения будет уменьшаться.
Ответ: 223.
Ответ: 223
Гость
30.03.2016 14:11
за даче написано на двойном фокусном расстоянии, а не за двойным (может я что-то не так понял)
Антон
«Как изменятся при удалении предмета от линзы следующие три величины: (...)»
Установите соответствие между оптическими приборами и разновидностями изо-бражений, которые они дают. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| A | Б |
Пояснение .
Выполняя это задание, полезно задать себе наводящий вопрос: какими лучами удобно воспользоваться для построения изображения в случае названных двух приборов? Ответ на него поможет решить два других вопроса:
1) изображение прямое или перевернутое?
2) оно действительное или мнимое?
Ответы на них очевидны - при условии, что вы представляете себе, что такое плоское зеркало и как устроен простейший фотоаппарат.
Решение.
Плоское зеркало дает прямое мнимое изображение (А — 1). Объектив простейшего фотоаппарата представляет собой собирающую линзу, которая дает действительное изображение на фотопластинке. При этом изображение получается перевернутым. Следовательно, правильный ответ среди перечисленных: Б — 2.
Ответ: 12.
Ответ: 12
Луч света падает на границу раздела «стекло - воздух». Как изменятся при увеличении показателя преломления стекла следующие три величины: длина волны света в стекле, угол преломления, угол полного внутреннего отражения?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение.
При переходе светового пучка из стекла в воздух частота электромагнитных колебаний в световой волне не изменяется, поскольку она не зависит от того, в какой среде распространяется волна. Длина волны связана с частотой электромагнитных колебаний и скоростью распространения соотношением При увеличении показателя преломления, скорость распространения световой волны в среде уменьшается, а значит, уменьшается и длина волны света в стекле. Согласно закону преломления Снеллиуса, синусы углов падения и преломления при выходе света из стекла в воздух связаны с показателем преломления стекла соотношением Следовательно, при увеличении показателя преломления, угол преломления будет увеличиваться. Наконец, угол полного внутреннего отражения определяется соотношением Таким образом, увеличение приведет к уменьшению угла полного внутреннего отражения.
Геометрическая оптика основывается на представлении о прямолинейном распространении света. Главную роль в ней играет понятие светового луча. В волновой оптике световой луч совпадает с направлением нормали к волновому фронту, а в корпускулярной - с траекторией движения частицы. В случае точечного источника в однородной среде световые лучи представляют собой прямые линии, выходящие из источника во всех направлениях. На границах раздела однородных сред направление световых лучей может изменяться вследствие отражения или преломления, но в каждой из сред они остаются прямыми. Также в соответствии с опытом принимается, что при этом направление световых лучей не зависит от интенсивности света.
Отражение.
Когда свет отражается от полированной плоской поверхности, угол падения (измеренный от нормали к поверхности) равен углу отражения (рис. 1), причем отраженный луч, нормаль и падающий луч лежат в одной плоскости. Если на плоское зеркало падает световой пучок, то при отражении форма пучка не изменяется; он лишь распространяется в другом направлении. Поэтому, глядя в зеркало, можно видеть изображение источника света (или освещенного предмета), причем изображение кажется таким же, как и исходный объект, но находящимся за зеркалом на расстоянии, равном расстоянию от объекта до зеркала. Прямая, проходящая через точечный объект и его изображение, перпендикулярна зеркалу.
Многократное отражение.
Когда два зеркала обращены одно к другому, изображение, возникающее в одном из них, отражается в другом, и получается целый ряд изображений, число которых зависит от взаимного расположения зеркал. В случае двух параллельных зеркал, когда объект помещается между ними (рис. 2,а ), получается бесконечная последовательность изображений, расположенных на прямой, перпендикулярной обоим зеркалам. Часть этой последовательности можно увидеть, если зеркала расположены друг от друга на достаточно большом расстоянии, чтобы можно было заглянуть со стороны. Если два плоских зеркала образуют прямой угол, то каждое из двух первичных изображений отражается во втором зеркале, но при этом вторичные изображения совпадают, так что в результате получится всего три изображения (рис. 2,б ). При меньших углах между зеркалами можно получить большее число изображений; все они расположены на окружности, проходящей через объект, с центром в точке на линии пересечения зеркал. Изображения, которые дают плоские зеркала, всегда мнимые - они не формируются реальными световыми пучками и потому не могут быть получены на экране.
Отражение от кривых поверхностей.
Отражение от кривых поверхностей происходит по тем же законам, что и от прямых, причем нормаль в точке отражения проводится перпендикулярно касательной плоскости в этой точке. Простейший, но самый важный случай - отражение от сферических поверхностей. В этом случае нормали совпадают с радиусами. Здесь возможны два варианта:
1. Вогнутые зеркала: свет падает изнутри на поверхность сферы. Когда пучок параллельных лучей падает на вогнутое зеркало (рис. 3,а ), отраженные лучи пересекаются в точке, расположенной на половине расстояния между зеркалом и центром его кривизны. Эта точка называется фокусом зеркала, а расстояние между зеркалом и этой точкой - фокусным расстоянием. Расстояние s от объекта до зеркала, расстояние s ў от зеркала до изображения и фокусное расстояние f связаны формулой
1/f = (1/s ) + (1/s ў ),
где все величины следует считать положительными, если их измерять влево от зеркала, как на рис. 4,а . Когда объект находится на расстоянии, превышающем фокусное, формируется действительное изображение, но когда расстояние s меньше фокусного расстояния, расстояние до изображения s ў становится отрицательным. При этом изображение формируется за зеркалом и является мнимым.
2. Выпуклые зеркала: свет падает извне на поверхность сферы. В этом случае после отражения от зеркала всегда получается расходящийся пучок лучей (рис. 3,б ), а изображение, образующееся за зеркалом, всегда мнимое. Положение изображений можно определить, пользуясь той же формулой, взяв в ней фокусное расстояние со знаком «минус».
На рис. 4,а показано вогнутое зеркало. Слева в виде вертикальной стрелки изображен объект высотой h . Радиус сферического зеркала равен R , а фокусное расстояние f = R /2. В этом примере расстояние s от зеркала до объекта больше R . Изображение можно построить графически, если из бесконечно большого числа световых лучей рассмотреть три, исходящие из вершины объекта. Луч, параллельный главной оптической оси, после отражения от зеркала пройдет через фокус. Второй луч, попадающий в центр зеркала, отразится таким образом, что падающий и отраженный лучи образуют одинаковые углы с главной осью. Пересечение этих отраженных лучей даст изображение верхней точки объекта, а полное изображение объекта можно получить, если из этой точки опустить перпендикуляр h ў на главную оптическую ось. Для проверки можно проследить за ходом третьего луча, идущего через центр кривизны зеркала и отражающегося от него обратно по тому же самому пути. Как видно из рисунка, он тоже пройдет через точку пересечения первых двух отраженных лучей. Изображение в этом случае будет действительным (оно формируется настоящими световыми пучками), перевернутым и уменьшенным.
То же самое зеркало представлено на рис. 4,б , но расстояние до объекта меньше фокусного. В этом случае после отражения лучи образуют расходящийся пучок, а их продолжения пересекаются в точке, которую можно рассматривать как источник, из которого выходит весь пучок. Изображение будет мнимым, увеличенным и прямым. Случаю, представленному на рис. 4,б , соответствует вогнутое зеркало для бритья, если объект (лицо) располагается в пределах фокусного расстояния.
Видеть сквозь стеныВ девяностых годах прошлого века продавался любопытный прибор под громким названием: «рентгеновский аппарат». Помню, как я был озадачен, когда еще школьником впервые взял в руки эту остроумную выдумку: трубка давала возможность видеть буквально сквозь непрозрачные предметы!
Рис. 95. Мнимый рентгеновский аппарат.
Я различал окружающее не только через толстую бумагу, но и через лезвие ножа, непроницаемое даже для подлинных рентгеновских лучей. Нехитрый секрет устройства этой игрушки сразу станет вам ясен, если вы взглянете на рис. 95, изображающий прообраз описываемой трубки. Четыре зеркальца, наклоненных под углом в 45°, отражают лучи несколько раз, ведя их, так сказать, в обход непрозрачного предмета.

Рис. 96. Перископ.
Рис. 97. Схема перископа подводной лодки.
В военном деле широко пользуются подобными же приборами. Сидя в траншее, можно следить за неприятелем, не поднимая головы над землей и, следовательно, не подставляя себя под огонь неприятеля, если смотреть в прибор, который называется «перископом» (рис. 96).
Чем длиннее путь лучей света от места вступления в перископ до глаза наблюдателя, тем меньше поле зрения, видимое в прибор. Чтобы увеличить поле зрения, применяется система оптических стекол. Однако стекла поглощают часть света, проникающего в перископ; ясность видимости предметов от этого страдает. Сказанное ставит известные границы высоте перископа; два десятка метров уже являются высотой, приближающейся к пределу; более высокие перископы дают чересчур малое поле зрения и неотчетливые изображения, особенно в пасмурную погоду.
Капитан подводной лодки наблюдает за атакуемым судном также посредством перископа - длинной трубки, конец которой выступает над водой. Эти перископы гораздо сложнее, чем сухопутные, но сущность та же: лучи отражаются от зеркала (или призмы), укрепленного в выступающей части перископа, идут вдоль трубы, отражаются в нижней ее части и попадают в глаз наблюдателя (рис. 97).
Говорящая «отрубленная» голова«Чудо» это нередко показывалось в странствующих по провинции «музеях» и «паноптикумах». Непосвященного оно положительно ошеломляет: вы видите перед собой небольшой столик с тарелкой, а на тарелке лежит… живая человеческая голова, которая двигает глазами, говорит, ест! Под столиком спрятать туловище как будто негде. Хотя подойти вплотную к столу нельзя, - вас отделяет от него барьер, - все же вы ясно видите, что под столом ничего нет.

Рис. 98. Секрет «отрубленной» головы.
Когда вам придется быть свидетелем такого «чуда», попробуйте закинуть в пустое место под столиком скомканную бумажку. Загадка сразу разъяснится: бумажка отскочит от… зеркала! Если она и не долетит до стола, то все же обнаружит существование зеркала, так как в нем появится ее отражение (рис. 98).
Достаточно поставить по зеркалу между ножками стола, чтобы пространство под ним казалось издали пустым, - разумеется, в том лишь случае, если в зеркале не отражается обстановка комнаты или публика. Вот почему комната должна быть пуста, стены совершенно одинаковы, пол выкрашен в однообразный цвет, без узоров, а публика держится от зеркала на достаточном расстоянии.
Секрет прост до смешного, но пока не узнаешь, в чем он заключается, прямо теряешься в догадках.
Иногда фокус обставляется еще эффектнее. Фокусник показывает сначала пустой столик: ни под ним, ни над ним ничего нет. Затем приносится из-за сцены закрытый ящик, в котором будто бы и хранится «живая голова без туловища» (в действительности же ящик пустой). Фокусник ставит этот ящик на стол, откидывает переднюю стенку, - и изумленной публике представляется говорящая человеческая голова. Читатель, вероятно, уже догадался, что в верхней доске стола имеется откидная часть, закрывающая отверстие, через которое сидящий под столом, за зеркалами, просовывает голову, когда на стол ставят пустой ящик без дна. Фокус видоизменяют и на иной лад, но перечислять все варианты мы здесь не станем; увидев, читатель разгадает их сам.
Впереди или сзади?Есть не мало вещей домашнего обихода, с которыми многие люди обращаются нецелесообразно. Мы уже указывали раньше, что иные не умеют пользоваться льдом для охлаждения: ставят охлаждаемые напитки на лед, вместо того чтобы помещать их под лед. Оказывается, что и обыкновенным зеркалом не все умеют пользоваться. Сплошь и рядом, желая хорошо разглядеть себя в зеркале, ставят лампу позади себя, чтобы «осветить свое отражение», вместо того чтобы осветить самих себя! Многие женщины поступают именно таким образом. Наша читательница, без сомнения, догадается поместить лампу впереди себя.
Можно ли видеть зеркало?Вот еще доказательство недостаточного знакомства нашего с обыкновенным зеркалом: на поставленный в заголовке вопрос большинство отвечает неправильно, хотя все глядятся в зеркало ежедневно.
Те, кто убежден, что зеркало можно видеть, ошибаются. Хорошее чистое зеркало невидимо. Можно видеть раму зеркала, его края, предметы, в нем отражающиеся, но самого зеркала, если только оно не загрязнено, видеть нельзя. Всякая отражающая поверхность, в отличие от поверхности рассеивающей , сама по себе невидима. (Рассеивающей называется такая поверхность, которая разбрасывает лучи света по всевозможным направлениям. В общежитии мы называем отражающие поверхности полированными, а рассеивающие - матовыми.)
Все трюки, фокусы и иллюзии, основанные на использовании зеркал, - хотя бы, например, сейчас описанный опыт с головой, - основаны именно на том, что само зеркало невидимо, а видны лишь отражающиеся в нем предметы.
Кого мы видим, глядя в зеркало?«Разумеется, самих себя, - ответят многие, - наше изображение в зеркале есть точнейшая копия нас самих, сходная с нами во всех подробностях».
Не угодно ли, однако, убедиться в этом сходстве? У вас на правой щеке родинка - у вашего двойника правая щека чиста, но на левой щеке есть пятнышко, которого у вас на этой щеке не имеется. Вы зачесываете волосы направо - ваш двойник зачесывает их налево. У вас правая бровь выше и гуще левой; у него, напротив, эта бровь ниже и реже, нежели левая. Вы носите часы в правом кармане жилета, а записную книжку в левом кармане пиджака; ваш зеркальный двойник имеет иные привычки: его записная книжка хранится в правом кармане пиджака, часы - в левом жилетном. Обратите внимание на циферблат его часов. У вас таких часов никогда не бывало: расположение и начертание цифр на них необычайное; например, цифра восемь изображена так, как ее нигде не изображают - IIX, и помещена на месте двенадцати; двенадцати же нет совсем; после шести следует пять, и т. д.; кроме того, движение стрелок на часах вашего двойника обратно обычному.
Рис. 99. Такие часы имеет при себе двойник, которого вы видите в зеркале.
Наконец, у вашего зеркального двойника есть физический недостаток, от которого вы, надо думать, свободны: он левша. Он пишет, шьет, ест левой рукой, и если вы выразите готовность с ним поздороваться, он протянет вам левую руку.
Нелегко решить, грамотен ли ваш двойник. Во всяком случае грамотен как-то по особенному. Едва ли удастся вам прочесть хоть одну строку из той книги, которую он держит, или какое-нибудь слово в тех каракулях, которые он выводит своей левой рукой.
Таков тот человек, который притязает на полное сходство с вами! А вы хотите судить по нему о внешнем виде вас самих…
Шутки в сторону: если вы думаете, что, глядя в зеркало, видите самих себя, - вы заблуждаетесь. Лицо, туловище и одежда у большинства людей не строго симметричны (хотя мы этого обычно не замечаем): правая половина не вполне сходна с левой. В зеркале все особенности правой половины переходят к левой, и наоборот, так что перед нами является фигура, производящая зачастую совсем иное впечатление, чем наша собственная.
Рисование перед зеркаломНетождественность зеркального отражения с оригиналом еще заметнее выступает в следующем опыте.
Поставьте перед собой отвесно на стол зеркало, положите перед ним бумажку и попробуйте нарисовать на ней какую-нибудь фигуру, например прямоугольник с диагоналями. Но не смотрите при этом прямо на свою руку, а следите лишь за движениями руки, отраженной в зеркале.
Вы убедитесь, что столь легкая на вид задача почти невыполнима. В течение многих лет наши зрительные впечатления и двигательные ощущения успели прийти в определенное соответствие. Зеркало нарушает эту связь, так как представляет глазам движения нашей руки в искаженном виде. Давнишние привычки будут протестовать против каждого вашего движения: вы хотите провести линию вправо, а рука тянет влево, и т. п.

Рис. 100. Рисование перед зеркалом.
Еще больше неожиданных странностей вы встретите, если вместо простого чертежа попробуете рисовать перед зеркалом более сложные фигуры или писать что-нибудь, глядя на строки в зеркале: выйдет комичная путаница!
Те отпечатки, которые получаются на пропускной бумаге, - тоже изображения зеркально симметричные. Рассмотрите надписи, испещряющие вашу пропускную бумагу, и попробуйте прочесть их. Вам не разобрать ни одного слова, даже вполне отчетливого: буквы имеют необычный наклон влево, а главное, последовательность штрихов в них не та, к какой вы привыкли. Но приставьте к бумаге зеркало под прямым углом - и вы увидите в нем все буквы написанными так, как вы привыкли их видеть. Зеркало дает симметричное отражение того, что само является симметричным изображением обыкновенного письма.
Расчетливая поспешностьМы знаем, что в однородной среде свет распространяется прямолинейно, т. е. скорейшим путем. Но свет избирает скорейший путь также и в том случае, когда не идет от одной точки к другой непосредственно, а достигает ее, предварительно отразившись от зеркала.
Проследим за его путем. Пусть буква A на рис. 101 обозначает источник света, линия MN - зеркало, а линия АВС - путь луча от свечи до глаза C. Прямая KB перпендикулярна к MN.
По законам оптики угол отражения 2 равен углу падения 1. Зная это, легко доказать, что из всех возможных путей от A к C, с попутным достижением зеркала MN, путь АВС - самый скорый. Для этого сравним путь луча АВС с каким-нибудь другим, например с ADC (рис. 102). Опустим перпендикуляр АЕ из точки A на MN и продолжим его далее до пересечения с продолжением луча ВС в точке F. Соединим также точки F и D. Убедимся, прежде всего, в равенстве треугольников ABE и EBF. Они - прямоугольные, и у них общий катет ЕВ; кроме того, углы EFB и ЕАВ равны между собой, так как соответственно равны углам 2 и 1. Следовательно, AE = EF. Отсюда вытекает равенство прямоугольных треугольников AED и EDF по двум катетам и, следовательно, равенство AD и DF.
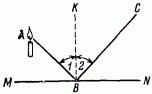
Рис. 101. Угол отражения 2 равен углу падения 1.
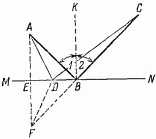
Рис. 102. Свет, отражаясь, избирает кратчайший путь.
Ввиду этого мы можем путь АВС заменить равным ему путем CBF (так как AB = FB), a путь ADC - путем CDF. Сравнивая же между собой длины CBF и CDF, видим, что прямая линия CBF короче ломаной CDF. Отсюда путь АВС короче ADC, что и требовалось доказать!
Где бы ни находилась точка D, путь АВС всегда будет короче пути ADC, если только угол отражения равен углу падения. Значит, свет действительно избирает самый короткий и самый скорый путь из всех возможных между источником, зеркалом и глазом. На это обстоятельство впервые указал еще Герон Александрийский, замечательный греческий механик и математик II века.
Полет вороныУменье находить кратчайший путь в случаях, подобных сейчас рассмотренным, может пригодиться для решения некоторых головоломок. Вот пример одной из таких задач.
На ветке дерева сидит ворона. Внизу на дворе рассыпаны зерна. Ворона спускается с ветки, схватывает зерно и садится на забор. Спрашивается, где должна она схватить зерно, чтобы путь ее был кратчайшим (рис. 103).

Рис. 103. Задача о вороне. Найти кратчайший путь до забора.
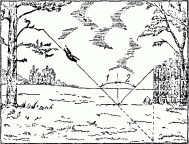
Рис. 104. Решение задачи о вороне.
Задача эта совершенно сходна с той, которую мы только что рассмотрели. Нетрудно поэтому дать правильный ответ: ворона должна подражать лучу света, т. е. лететь так, чтобы угол 1 был равен углу 2 (рис. 104). Мы уже видели, что в таком случае путь оказывается кратчайшим.
Новое и старое о калейдоскопеВсем известна хорошая игрушка, носящая название калейдоскопа: горсточка пестрых осколков отражается в двух или трех плоских зеркальцах и образует удивительно красивые фигуры, разнообразно меняющиеся при малейшем повороте калейдоскопа. Хотя калейдоскоп довольно общеизвестен, мало кто подозревает, какое огромное число разнообразных фигур можно получить с его помощью. Допустим, вы держите в руках калейдоскоп с 20 стеклышками и 10 раз в минуту поворачиваете его, чтобы получить новое расположение отражающихся стеклышек. Сколько времени понадобится вам, чтобы пересмотреть все получающиеся при этом фигуры?
Самое пылкое воображение не предусмотрит правильного ответа на этот вопрос. Океаны высохнут и горные цепи сотрутся, прежде чем будут исчерпаны все узоры, чудесным образом скрытые внутри вашей маленькой игрушки, потому что для осуществления всех их понадобится по крайней мере 500000 миллионов лет. Свыше пятисот миллионов тысячелетий нужно вращать наш калейдоскоп, чтобы пересмотреть все его узоры!

Рис. 105. Калейдоскоп.
Бесконечно разнообразные, вечно меняющиеся узоры калейдоскопа давно интересуют декораторов-художников, фантазия которых не может соперничать с неистощимой изобретательностью этого прибора. Калейдоскоп создает подчас узоры поразительной красоты, могущие служить прекрасными мотивами для орнаментов на обоях, для узоров на различных тканях и т. п.
Но в широкой публике калейдоскоп не вызывает уже того живого интереса, с каким встречен он был лет сто назад, когда был еще новинкой. Его воспевали в прозе и стихах.
Калейдоскоп изобретен был в Англии в 1816 г. и через год-полтора проник уже в Россию, где был встречен с восхищением. Баснописец А. Измайлов в журнале «Благонамеренный» (июль 1818 г.) писал о калейдоскопе в следующих выражениях:
«Прочитав объявление о калейдоскопе, достаю сие чудесное орудие -
Смотрю - и что ж в моих глазах?
В фигурах разных и звездах
Сапфиры, яхонты, топазы,
И изумруды, и алмазы,
И аметисты, и жемчуг,
И перламутр - все вижу вдруг!
Лишь сделаю рукой движенье -
И новое в глазах явленье!
Не только в стихах, но и в прозе невозможно описать того, что видишь в калейдоскопе. Фигуры переменяются при каждом движении руки и одна на другую не походят. Какие прелестные узоры! Ах, если бы можно было вышивать их на канве! Но где взять такие яркие шелка? Вот самое приятное занятие от безделия и от скуки. Гораздо лучше смотреть в калейдоскоп, нежели раскладывать грандпасьянс.
Утверждают, будто калейдоскоп известен был еще в XVII столетии. Ныне недавно он возобновлен и усовершенствован в Англии, оттуда месяца два назад перешел во Францию. Один из тамошних богачей заказал калейдоскоп в 20 000 франков. Вместо разноцветных стеклышек и бус велел он положить жемчуг и драгоценные каменья».
«Известный своими превосходными оптическими инструментами императорский физико-механик Роспини делает и продает калейдоскопы по 20 руб. Без сомнения, гораздо более найдется на них охотников, нежели на физические и химические лекции, от которых - к сожалению и удивлению - благонамеренный господин Роспини не получил никакой себе выгоды».
Долго калейдоскоп оставался не более чем любопытной игрушкой и только в наши дни получил полезное применение для составления узоров. Изобретен прибор, с помощью которого можно фотографировать калейдоскопические узоры и, таким образом, механически придумывать всевозможные орнаменты.
Дворцы иллюзий и миражей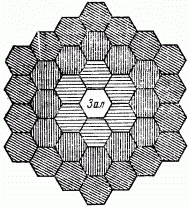
Рис. 106. Троекратное отражение стен центрального зала дает 36 зал.
Какие ощущения испытали бы мы, если бы, уменьшенные до размеров стеклянного осколка, очутились внутри калейдоскопа? Существует способ выполнить такой опыт на деле. Эту чудесную возможность имели в 1900 г. посетители всемирной Парижской выставки, где большим успехом пользовался так называемый «Дворец иллюзий» - нечто вроде калейдоскопа, но только неподвижного. Вообразите шестиугольный зал, каждая стена которого представляет собой огромное зеркало идеальной полировки. В углах зеркального зала устроены архитектурные украшения в виде колонн и карнизов, сливающихся с лепкой потолка. Зритель внутри такого зала видел себя словно затерянным в невообразимой толпе похожих на него людей в бесконечной анфиладе зал к колонн; они окружали его со всех сторон и простирались вдаль, насколько видел глаз. Залы, заштрихованные на рис. 106 горизонтально, получаются вследствие однократного отражения; в результате двукратного отражения получаются изображения, заштрихованные перпендикулярно к первым, т. е, еще 12 залов. Троекратное отражение присоединяет к ним еще 18 залов (косая штриховка); залы множатся с каждым отражением, и общее число их зависит от совершенства полировки и от параллельности зеркал, занимающих противоположные грани призматического зала. Практически различались еще залы, получавшиеся в результате 12-го отражения, т. е. видимый горизонт обнимал 468 залов.
Причина «чуда» ясна всякому, кто знаком с законами отражения света: ведь тут имеются три пары параллельных зеркал и десять пар зеркал, поставленных под углом; неудивительно, что они дают такое множество отражений. Еще любопытнее те оптические эффекты, которые были достигнуты на Парижской выставке в так называемом «Дворце миражей». Устроители этого «дворца» присоединили к бесчисленным отражениям еще мгновенную перемену всей картины. Они как бы устроили подвижный, огромных размеров калейдоскоп, внутри которого помещались зрители.
Перемена обстановки в этом «Дворце миражей» достигалась следующим образом: зеркальные стены на некотором расстоянии от ребер разрезаны вдоль, и полученный угол может вращаться вокруг оси, заменяясь другим. Из рис. 107 видно, что можно произвести три замены, соответствующие углам 1, 2 и 3. Теперь представьте себе, что все углы, обозначенные цифрой 1, заключают в себе обстановку тропического леса, все углы 2 - обстановку арабского зала, а углы 3 - индийского храма.
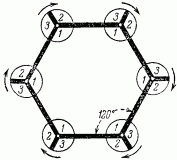
Рис. 108. Секрет «Дворца миражей».
Одним движением скрытого механизма, поворачивающего углы, тропический лес превращается в храм или в арабский зал. Весь секрет «волшебства» основан на таком простом физическом явлении, как отражение световых лучей.
Почему и как преломляется свет?То, что при переходе из одной среды в другую луч света преломляется, многим представляется странным капризом природы. Кажется непонятным, почему свет не сохраняет в новой среде первоначального своего направления, а избирает ломаный путь. Кто так думает, тот, вероятно, с удовлетворением узнает, что луч света претерпевает, в сущности, то же самое, что происходит и с марширующей колонной бойцов, пересекающей границу между почвой, удобной для ходьбы, и почвой неудобной. Вот что говорит об этом Джон Гершель, знаменитый астроном и физик прошлого века.
«Представьте себе отряд солдат, идущий по местности, разделенной прямой границей на две полосы, из которых одна гладкая, ровная и удобная для ходьбы, другая - кочковатая, затруднительная, так что ходьба по ней не может совершаться столь быстро. Предположим сверх того, что фронт отряда составляет угол с пограничной линией между двумя полосами, так что солдаты достигают этой границы не все одновременно, а последовательно один за другим. Тогда каждый солдат, переступив границу, очутится на почве, по которой он не может более подвигаться так быстро, как до того времени. Он не сможет уже держаться на одной линии с остальной частью шеренги, еще находящейся на лучшей почве, и будет от нее отставать с каждой секундой все больше. Так как каждый солдат, достигая границы, испытывает одинаковое затруднение в ходьбе, то если солдаты не нарушат строя, не рассеются, а будут продолжать маршировать правильной колонной, вся та часть колонны, которая переступила границу, будет неизбежно отставать от остальной и составит с ней поэтому тупой угол в точке пересечения границы. И так как необходимость ходить в ногу, не перебивая дороги друг другу, заставит каждого солдата шагать прямо перед собой, под прямым углом к новому фронту, то путь, который он пройдет по переходе границы, будет, во-первых, перпендикулярен к новому фронту, а во-вторых, так относиться к тому пути, какой был бы пройден в случае отсутствия замедления, как новая скорость к прежней».
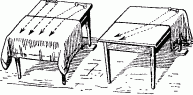
Рис. 109. Опыт, поясняющий преломление света.
В малом виде вы можете воспроизвести это наглядное подобие преломления света у себя на столе. Накройте половину стола скатертью (рис. 109) и, слегка наклонив стол, заставьте скатываться по нему пару колесиков, наглухо посаженных на общую ось (например, от сломанного детского паровоза или другой игрушки). Если направление движения колес и край скатерти составляют прямой угол, преломления пути не происходит. Вы имеете в этом случае иллюстрацию оптического правила: луч, перпендикулярный к плоскости раздела сред, не преломляется. При направлении, наклонном к краю скатерти, путь колес изламывается на этом краю, т. е. на границе между средами с различной скоростью движения в них. Легко заметить, что при переходе из части стола, где скорость движения больше (непокрытая часть), в ту часть, где скорость меньше (скатерть), направление пути («луч») приближается к «перпендикуляру падения». В обратном случае наблюдается удаление от этого перпендикуляра.
Из этого можно, между прочим, почерпнуть важное указание, вскрывающее сущность рассматриваемого явления, а именно, что преломление обусловлено различием скорости света в обеих средах. Чем больше различие в скорости, тем значительнее преломление; так называемый «показатель преломления», характеризующий величину излома лучей, есть не что иное, как отношение этих скоростей. Когда вы читаете, что показатель преломления при переходе из воздуха в воду есть 4/3, то вы, вместе с тем, узнаёте, что свет движется в воздухе примерно в 1,3 раза скорее, чем в воде.
А в связи с этим находится и другая поучительная особенность распространения света. Если в случае отражения световой луч следует кратчайшим путем, то в случае преломления он избирает скорейший путь: никакое другое направление не приводит луч так скоро к «месту назначения», как этот изломанный путь.
Когда длинный путь проходится быстрее, чем короткий?Но неужели ломаный путь может быстрее привести к цели, чем прямой? Да, в тех случаях, когда скорость движения в различных частях пути различна. Вспомните, что приходится делать жителям деревни, расположенной между двумя железнодорожными станциями в соседстве с одной из них. Чтобы попасть скорее на дальнюю станцию, они едут на лошади сначала в обратном направлении, к ближайшей станции, там садятся в поезд и едут на место назначения. Им короче было бы, разумеется, прямо ехать туда на лошади, но они предпочитают более длинный путь на лошади и в вагоне, потому что он приводит к цели скорее.

Рис. 110. Задача о кавалеристе. Найти скорейший путь из A в С.
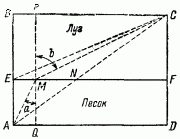
Рис. 111. Решение задачи о кавалеристе. Скорейший путь АМС.
Уделим минуту внимания еще одному примеру. Кавалерист должен прибыть с донесением из точки А к палатке командира в точке C (рис. 110). Его отделяют от палатки полоса глубокого песка и полоса луга, разграниченные между собой прямой линией EF. По песчаной почве лошадь движется вдвое медленнее, чем по лугу. Какой же путь должен выбрать кавалерист, чтобы достигнуть палатки в кратчайшее время?
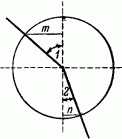
Рис. 112. Что такое синус? Отношение m к радиусу есть синус угла 1, отношение n к радиусу - синус угла 2.
На первый взгляд кажется, что самый скорый путь - прямая линия, проведенная от A до С. Но это совершенно ошибочно, и я не думаю, чтобы нашелся кавалерист, который выбрал бы такой путь. Медленное движение по песку наведет его на правильную мысль сократить эту медленную часть пути, прорезав песчаную полосу по менее косой линии; конечно, тем самым удлинится вторая часть пути - по лугу; но так как по лугу можно двигаться вдвое быстрее, то удлинение пути не перевесит полученной выгоды, и в общем итоге путь будет проделан в меньший промежуток времени. Другими словами, путь кавалериста должен преломиться на границе обоих родов почвы и притом так, чтобы путь по лугу составлял с перпендикуляром к границе больший угол, чем путь по песчаной почве.
Кто знаком с геометрией, именно с теоремой Пифагора, тот может проверить, что прямой путь AC действительно не является путем скорейшим и что при тех размерах для ширины полос и расстояний, которые мы здесь имеем в виду, можно скорее достичь цели, если направиться, например, по ломаной АЕС (рис. 111).
На рис. 110 указано, что ширина песчаной полосы 2 км, луговой - 3 км, а расстояние ВС - 7 км. Тогда вся длина AC (рис. 111) равна, по теореме Пифагора, корень(52 + 72) = корень(74) = 8,60 км. Часть AN - путь по песку - этого отрезка составляет, как легко сообразить, 2/5 этой величины, т. е. 3,44 км. Так как по песку движение происходит вдвое медленнее, чем по лугу, то 3,44 км песчаного пути равнозначны, в смысле требуемого времени, 6,88 км по лугу. И, следовательно, весь смешанный путь по прямой АС, равный 8,60 км, соответствует 12,04 км пути по лугу.
Сделаем такое же «приведение к лугу» и для ломаного пути АЕС. Часть АЕ = 2 км и соответствует 4 км пути по лугу. Часть ЕС = корень(32 + 72) = корень(58) = 7,61 км. Итого весь ломаный путь AEC отвечает 4 + 7,61 = 11,61 км.
Итак, «короткий» прямой путь соответствует 12,04 км движения по лугу, а «длинный» ломаный - всего только 11,61 км по той же почве. «Длинный» путь, как видите, дает выгоду в 12,04–11,61 = 0,43, почти в полкилометра!
Но мы не указали еще самого быстрого пути. Быстрейший путь, как учит теория, будет тот, при котором (нам придется здесь обратиться к услугам тригонометрии) синус угла b относится к синусу угла A, как скорость на лугу относится к скорости на песке, т. е. как 2:1. Другими словами, нужно выбрать направление так, чтобы sin b был вдвое больше sin а. Для этого нужно перешагнуть границу между полосами в такой точке m, которая находится в одном километре от Е. Действительно, тогда sin b = 6/(корень(32 + 62)), sin a = 1/(корень(1 + 22)), отношение sin b/sin a = (6/корень(45))/(1/ (3*корень(5))) = (6/(3*корень(5)))/(1/корень(5)) = 2, т. е. как раз отношению скоростей.
А какова будет в таком случае «приведенная к лугу» длина пути? Вычислим: AM = корень(22 + 12), что отвечает 4,47 км пути по лугу. МС = корень(45) = 6,71 км. Длина всего пути 4,47 + 6,71 = 11,18, т. е. на 860 км короче прямолинейного пути, который, как мы уже знаем, соответствует 12,04 км.
Вы видите, какие выгоды доставляет при данных условиях изламывание пути. Световой луч как раз и избирает такой скорейший путь, потому что закон преломления света строго удовлетворяет требованию математического решения задачи: синус угла преломления относится к синусу угла падения, как скорость света в новой среде к скорости его в покидаемой среде; с другой стороны, это отношение равно показателю преломления света в указанных средах.
Объединяя в одно правило особенности и отражения и преломления, мы можем сказать, что световой луч во всех случаях следует по быстрейшему пути, т. е. подчиняется правилу, которое физики называют «принципом скорейшего прихода» (принцип Ферма).
Если среда неоднородна и ее преломляющая способность меняется постепенно, как, например, в нашей атмосфере, то и в таком случае вполне осуществляется быстрейший приход. Этим объясняется то небольшое искривление лучей небесных светил в атмосфере, которое на языке астрономов называется «атмосферной рефракцией». В атмосфере, постепенно уплотняющейся книзу, луч света изгибается так, что вогнутость его обращена к Земле. Тогда луч остается дольше в высоких слоях, которые слабее замедляют его путь, и проводит меньше времени в «медленных» низких слоях, в итоге он приходит к цели быстрее, чем по пути строго прямолинейному.
Принцип быстрейшего прихода (принцип Ферма) справедлив не для одних лишь световых явлений: ему в полной мере подчиняется также распространение звука и всех вообще волнообразных движений, какова бы ни была природа этих волн.
Читатель, без сомнения, желал бы узнать, чем объясняется это свойство волнообразных движений. Приведу поэтому относящиеся сюда соображения, высказанные выдающимся современным физиком Шредингером [В докладе, прочитанном в Стокгольме при получении Нобелевской премии (в 1933 г.)]. Он исходит из знакомого уже нам примера марширующих солдат и имеет в виду случай движения светового луча в среде постепенно изменяющейся плотности.
«Пусть, - пишет он, - для того, чтобы сохранить строгую правильность фронта, солдаты соединены длинным шестом, который каждый из них крепко удерживает в руках. Команда гласит: всем бежать возможно быстрее! Если характер почвы медленно меняется от точки к точке, то сначала, скажем, правое, а позднее левое крыло фронта будет подвигаться быстрее - и поворот фронта осуществится сам собой. Мы заметим при этом, что пройденный путь - не прямолинейный, а искривленный. То, что путь этот строго совпадает с кратчайшим в смысле времени прибытия в данный пункт при заданных свойствах почвы, - довольно понятно, так как ведь каждый солдат старался подвигаться как можно быстрее».
Новые РобинзоныБез сомнения, вы знаете, как герои романа Жюля Верна «Таинственный остров», заброшенные на необитаемую землю, добыли огонь без спичек и огнива. Робинзону явилась на помощь молния, зажегшая дерево, новым же Робинзонам Жюля Верна помогла не случайность, а находчивость сведущего инженера и твердое знание им законов физики. Помните, как удивился наивный моряк Пенкроф, когда, возвратившись с охоты, нашел инженера и журналиста перед пылающим костром.
«- Но кто же зажег огонь? - спросил моряк.
Солнце, - ответил Спилетт.
Журналист не шутил. Действительно, Солнце доставило огонь, которым так восторгался моряк. Он не верил своим глазам и был до того изумлен, что даже не мог расспрашивать инженера.
Значит, у вас было зажигательное стекло? - спросил инженера Герберт.
Нет, но я его изготовил.
И он его показал. Это были просто два стекла, снятые инженером со своих часов и часов Спилетта. Он соединил их края глиной, предварительно наполнив водой, и таким образом получилась настоящая зажигательная чечевица, с помощью которой, сосредоточив солнечные лучи на сухом мхе, инженер добыл огонь».
Читатель пожелает, я думаю, узнать, зачем нужно заполнять водой пространство между часовыми стеклами: разве наполненная воздухом двояковыпуклая чечевица не сосредоточивает лучей?
Именно нет. Часовое стекло ограничено двумя параллельными (концентрическими) поверхностями - наружной и внутренней; а известно из физики, что, проходя через среду, ограниченную такими поверхностями, лучи почти не изменяют своего направления. Проходя затем через второе такое же стекло, они и здесь не отклоняются, а следовательно, не собираются в фокусе. Чтобы сосредоточить лучи в одной точке, необходимо заполнить пространство между стеклами каким-нибудь прозрачным веществом, которое преломляло бы лучи сильнее, нежели воздух. Так и поступил инженер в романе Жюля Верна.
Обыкновенный графин с водой, если имеет шарообразную форму, также может служить зажигательной чечевицей. Это знали уже древние, которые заметили и то, что сама вода при этом остается холодной. Случалось даже, что стоящий на открытом окне графин с водой зажигал занавески, скатерть, обугливал стол. Те огромные шаровые бутылки с окрашенной водой, которые, по старинному обычаю, украшали раньше витрины аптек, могли быть иногда причиной настоящих катастроф, вызывая возгорание легко воспламеняющихся веществ, расположенных поблизости.
Небольшой круглой колбой, наполненной водой, можно даже при небольших размерах колбы довести до кипения воду, налитую на часовое стеклышко: для этого достаточна колба сантиметров в 12 диаметром. При 15 см в фокусе [Фокус помещается при этом весьма близко к колбе] получается температура 120°. Зажечь папироску с помощью колбы с водой так же легко, как и стеклянной чечевицей, о которой еще Ломоносов в своем стихотворении «О пользе стекла» писал:
Мы пламень солнечный стеклом здесь получаем
И Прометею тем безбедно подражаем.
Ругаясь подлости нескладных оных врак,
Небесным без греха огнем курим табак.
Следует заметить, однако, что зажигательное действие водяных линз значительно слабее, чем стеклянных. Это связано, во-первых, с тем, что преломление света в воде гораздо меньше, чем в стекле, во-вторых, вода в сильной степени поглощает инфракрасные лучи, которые играют большую роль в нагревании тел.
Любопытно, что зажигательное действие стеклянных чечевиц известно было еще древним грекам, более чем за тысячелетие раньше изобретения очков и зрительных труб. О нем упоминает Аристофан в знаменитой комедии «Облака». Сократ предлагает Стрептиаду задачу:
«Если бы кто писал обязательство на тебя в пяти талантах, как бы ты уничтожил оное?
Стрептиад. Нашел я, как истребить обязательство, да такой способ, что ты и сам признаешь его прехитрым! Видал ты, конечно, в аптеках камень прекрасный, прозрачный, которым зажигают?
Сократ. Зажигательное стекло?
Стрептиад. Точно так.
Стрептиад. Пока нотариус пишет, я, став позади его, направлю лучи Солнца на обязательство, да слова-то все и растоплю…»
Напомню для пояснения, что греки времен Аристофана писали на навощенных дощечках, которые от тепла легко растапливались.
Как добыть огонь с помощью льда?Материалом для двояковыпуклой линзы, а следовательно, и для добывания огня, может послужить также лед, если он достаточно прозрачен. При этом лед, преломляя лучи, сам не нагревается и не тает. Показатель преломления льда лишь немногим меньше, чем у воды, и если, как мы видели, можно добыть огонь с помощью шара, наполненного водой, то возможно сделать это и с помощью чечевицы из льда.
Ледяная чечевица сослужила хорошую службу в жюль-верновом «Путешествии капитана Гаттераса». Доктор Клоубони таким именно образом зажег костер, когда путники потеряли огниво и очутились без огня, при страшном морозе в 48 градусов.
- «Это несчастье, - сказал Гаттерас доктору.
Да, - отвечал тот.
У нас нет даже подзорной трубы, с которой мы могли бы снять чечевицу и добыть огня.
Знаю, - ответил доктор, - и очень жаль, что нет: солнечные лучи достаточно сильны, чтобы зажечь трут.
Что делать, придется утолить голод сырой медвежатиной, - заметил Гаттерас.
Да, - задумчиво проговорил доктор, - в крайнем случае. Но отчего бы нам не…
Что вы задумали? - полюбопытствовал Гаттерас.
Мне пришла в голову мысль…
Мысль? - воскликнул боцман. - Если вам пришла мысль, значит, мы спасены!
Не знаю, как удастся, - колебался доктор.
Что же вы придумали? - спросил Гаттерас.
У нас нет чечевицы, но мы ее изготовим.
Как? - поинтересовался боцман.
Отшлифуем из куска льда.
Неужели вы полагаете…
Отчего бы и нет? Ведь нужно только, чтобы лучи Солнца были сведены в одну точку, а для этой цели лед может заменить нам лучший хрусталь. Только я предпочел бы кусочек пресноводного льда: он крепче и прозрачнее.
Вот, если не ошибаюсь, эта ледяная глыба, - указал боцман на льдину шагах в ста от путешественников - судя по ее цвету, есть как раз то, что вам надо.
Вы правы. Возьмите-ка свой топор. Пойдемте друзья мои.
Все трое направились к указанной ледяной глыбе. Действительно, лед оказался пресноводным.
Доктор велел отрубить кусок льда, имеющий фут в диаметре и начал обравнивать его топором. Потом отделал его ножом, наконец постепенно отшлифовал рукою. Получилась прозрачная чечевица, словно из лучшего хрусталя. Солнце было довольно яркое. Доктор подставил чечевицу его лучам и сосредоточил их на труте. Через несколько секунд трут загорелся».

Рис 113. «Доктор сосредоточил лучи Солнца на труте».
Рассказ Жюля Верна не совсем фантастичен: опыты зажигания дерева при помощи ледяной чечевицы, впервые успешно выполненные в Англии с весьма большой чечевицей еще в 1763 г., с тех пор неоднократно производились с полным успехом. Конечно, трудно изготовить прозрачную ледяную чечевицу с помощью таких орудий, как топор, нож и «просто рука» (при 48-градусном морозе!), но можно изготовить ледяную чечевицу проще: налить воды в чашку надлежащей формы и заморозить, а затем, слегка подогрев чашку, вынуть из нее готовую чечевицу.

Рис. 114. Чашка для изготовления ледяной чечевицы.
Проделывая подобный опыт, не забывайте, что он удается лишь в ясный морозный день и на открытом воздухе, но не в комнате за оконным стеклом: стекло поглощает значительную часть энергии солнечных лучей и остающейся недостаточно, чтобы вызвать значительное нагревание.
С помощью солнечных лучейПроделайте еще опыт, тоже легко выполнимый в зимнее время. Положите на снег, заливаемый солнечным светом, два одинаковой величины лоскутка ткани, светлый и черный. Через час или два вы убедитесь, что черный лоскуток погрузился в снег, между тем как светлый остался на прежнем уровне. Доискаться причины подобного различия нетрудно: под черным лоскутком снег тает сильнее, так как темная ткань поглощает большую часть падающих на нее солнечных лучей; светлая же, напротив, большую часть их рассеивает и потому слабее нагревается, нежели черная.
Поучительный опыт этот впервые проделан был знаменитым борцом за независимость Соединенных Штатов Веньямином Франклином, обессмертившим себя, как физик, изобретением громоотвода. «Я взял у портного несколько квадратных кусочков сукна различных цветов, - писал он. - Между ними были: черный, темно-синий, светло-синий, зеленый, пурпуровый, красный, белый и различные другие цвета и оттенки. В одно светлое солнечное утро я положил все эти куски на снег. Через несколько часов черный кусок, нагревшийся сильнее других, погрузился так глубоко, что лучи Солнца более его не достигали; темно-синий погрузился почти настолько же, как и черный; светло-синий гораздо менее; остальные цвета опустились тем менее, чем они светлее. Белый же остался на поверхности, т. е. вовсе не опустился».
«К чему годна была бы теория, если бы из нее нельзя было извлечь никакой пользы? - восклицает он по этому поводу и продолжает: - Разве не можем мы из этого опыта вывести то, что черное платье в теплом солнечном климате менее годно, чем белое, так как оно на солнце сильнее нагревает наше тело, и если мы при этом еще будем делать движения, которые сами по себе нас согревают, то образуется излишняя теплота? Не должны ли мужские и женские летние шляпы быть белого цвета, чтобы устранить ту жару, которая вызывает у некоторых солнечный удар?… Далее, вычерненные стены не могут разве поглотить в течение дня столько солнечной теплоты, чтобы ночью остаться до некоторой степени теплыми и предохранить фрукты от мороза? Не может разве внимательный наблюдатель натолкнуться еще и на другие частности большей или меньшей важности?»
Каковы могут быть эти выводы и полезные применения, показывает пример немецкой южно-полярной экспедиции 1903 г. на корабле «Гаусс». Судно вмерзло в лед, и все обычные способы освобождения не привели ни к каким результатам. Взрывчатые вещества и пилы, пущенные в дело, удалили всего несколько сотен кубометров льда и не освободили корабля. Тогда обратились к помощи солнечных лучей: из темной золы и угля устроили на льду полосу в 2 км длины и в десяток метров ширины; она вела от корабля до ближайшей широкой щели во льду. Стояли ясные долгие дни полярного лета, и солнечные лучи сделали то, чего не могли сделать динамит и пила. Лед, подтаяв, сломался вдоль насыпанной полосы, и корабль освободился от льда.
Старое и новое о миражахВероятно, всем известно, в чем заключается физическая причина обыкновенного миража. Раскаленный зноем песок пустыни приобретает зеркальные свойства оттого, что прилегающий к нему нагретый слой воздуха имеет меньшую плотность, нежели вышележащие слои. Наклонный луч света от весьма далекого предмета, достигнув этого воздушного слоя, искривляет в нем свой путь так, что в дальнейшем следовании он вновь удаляется от земли и попадает в глаз наблюдателя, словно отразившись от зеркала под очень большим углом падения. И наблюдателю кажется, что перед ним расстилается в пустыне водная гладь, отражающая прибрежные предметы (рис. 115).
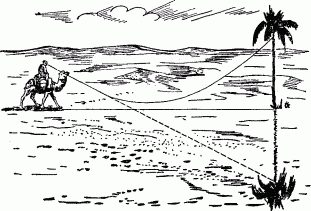
Рис. 115. Как возникает мираж в пустыне. Этот рисунок, обычно воспроизводимый в учебниках, представляет путь светового луча наклоненным к земле преувеличенно круто.
Правильнее было бы, впрочем, сказать, что нагретый слой воздуха близ раскаленной почвы отражает лучи не наподобие зеркала, а наподобие водной поверхности, рассматриваемой из глубины воды. Здесь происходит не простое отражение, а то, что на языке физики называется «внутренним отражением». Для этого необходимо, чтобы луч света вступал в воздушные слои очень полого - более полого, чем показано на нашем упрощенном рис. 115; иначе не будет превзойден «предельный угол» падения луча, а без этого не получается внутреннего отражения.
Отметим попутно один пункт этой теории, могущий породить недоразумение. Изложенное объяснение требует такого расположения воздушных слоев, при котором более плотные слои находились бы выше, чем менее плотные. Мы знаем, однако, что плотный, тяжелый воздух стремится опуститься и вытеснить лежащий под ним легкий слой газа вверх. Как же может существовать то расположение слоев плотного и разреженного воздуха, которое необходимо для появления миража?

Рис. 116. Мираж на гудронированном шоссе.
Разгадка кроется в том, что требуемое расположение воздушных слоев бывает не в неподвижном воздухе, а в воздухе, находящемся в движении. Нагретый почвой слой воздуха не покоится на ней, а непрерывно вытесняется вверх и тотчас сменяется новым слоем нагретого воздуха. Непрерывная смена обусловливает то, что к раскаленному песку всегда прилегает некоторый слой разреженного воздуха, пусть не одного и того же, но это уже безразлично для хода лучей.
Тот род миража, который мы рассматриваем, известен с древности. В современной метеорологии его называют «нижним» миражем (в отличие от «верхнего», порождаемого отражением лучей света слоями разреженного воздуха верхних областей атмосферы). Большинство людей убеждено, что этот классический мираж может наблюдаться только в знойном воздухе южных пустынь и не бывает в более северных широтах.
Между тем нижний мираж нередко случается наблюдать и в наших краях. Особенно часты подобные явления в летнее время на асфальтовых и гудронированных дорогах, которые благодаря темному цвету сильно нагреваются на солнце. Матовая поверхность дороги кажется тогда издали словно политой водой и отражает отдаленные предметы. Ход лучей света при этом мираже показан на рис. 116. При некоторой наблюдательности подобные явления можно видеть не так редко, как принято думать.
Есть и еще род миража - мираж боковой , о существовании которого обычно даже не подозревают. Это - отражение от нагретой отвесной стены. Такой случай описан одним французским автором. Приближаясь к форту крепости, он заметил, что ровная бетонная стена форта вдруг заблистала, как зеркало, отражая в себе окружающий ландшафт, почву, небо. Сделав еще несколько шагов, он заметил ту же перемену и с другой стеной форта. Казалось, будто серая неровная поверхность внезапно заменяется полированной. Стоял знойный день, и стены должны были сильно накалиться, в чем и заключалась разгадка их зеркальности. На рис. 117 показаны расположение стен форта (F и F") и местоположение наблюдателя (А и А"). Оказалось, что мираж наблюдается всякий раз, когда стена достаточно нагреется солнечными лучами. Удалось даже сфотографировать это явление.
На рис. 118 изображена (слева) стена F форта, сначала матовая, а затем блестящая (справа), как зеркало (снята из точки A"). На левом снимке - обыкновенный серый бетон, в котором, конечно, не могут отражаться стоящие близ стены фигуры двух солдат. Направо - та же стена в большей своей части приобрела зеркальные свойства, и ближайшая фигура солдата дает в ней свое симметричное изображение. Конечно, отражает лучи тут не сама поверхность стены, а лишь прилегающий к ней слой нагретого воздуха.
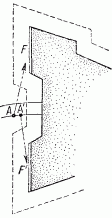
Рис. 117. План форта, где наблюдался мираж. Стена F казалась зеркальной из точки A, стена F" - из точки А"

Рис. 118. Серая неровная стена (слева) внезапно делается словно полированной, отражающей (справа).
В знойные летние дни следовало бы обращать внимание на накалившиеся стены больших зданий и искать, не обнаружатся ли явления миража. Без сомнения, при некотором внимании число замеченных случаев миража должно заметно участиться.
«Зеленый луч»«Наблюдали ли вы когда-нибудь Солнце, заходящее за горизонт моря? Да, без сомнения. Проследили ли вы за ним до того момента, когда верхний край диска соприкасается с линией горизонта и затем исчезает? Вероятно, да. Но заметили ли вы явление, происходящее в то мгновение, когда лучезарное светило бросает последний свой луч, если при этом небо свободно от облаков и совершенно прозрачно? Быть может, нет. Не пропускайте же случая сделать подобное наблюдение: в ваш глаз ударит не красный луч, а зеленый, дивного зеленого цвета, такого, какого ни один художник не может получить на своей палитре и какого не воспроизводит сама природа ни в разнообразных оттенках растительности, ни в цвете самого прозрачного моря».
Подобная заметка в одной английской газете привела в восторженное состояние молодую героиню романа Жюля Верна «Зеленый луч» и побудила ее предпринять ряд путешествий с единственной целью - собственными глазами увидеть зеленый луч. Юной шотландке не удалось, как повествует романист, наблюдать это красивое явление природы. Но оно все же существует. Зеленый луч - не легенда, хотя с ним и связано много легендарного. Это - явление, которым может восхищаться каждый любитель природы, если будет искать его с должным терпением.
Почему появляется зеленый луч?Вы поймете причину явления, если вспомните, в каком виде представляются нам предметы, когда мы смотрим на них сквозь стеклянную призму. Проделайте такой опыт: держите призму у глаза горизонтально широкой стороной вниз и рассматривайте через нее листок бумаги, приколотый на стене. Вы заметите, что листок, во-первых, поднялся значительно выше своего истинного положения, а во-вторых, имеет вверху фиолетово-синюю кайму, внизу - желто-красную. Поднятие зависит от преломления света, цветные каемки - от дисперсии стекла, т. е. свойства стекла неодинаково преломлять лучи разного цвета. Фиолетовые и синие лучи преломляются сильней прочих, поэтому мы видим вверху фиолетово-синюю кайму; красные преломляются всего слабее, и потому нижний край нашего бумажного листка имеет красную кайму.
Для лучшего понимания дальнейшего необходимо остановиться на происхождении этих цветных каемок. Призма разлагает белый свет, исходящий от бумаги, на все цвета спектра, давая множество цветных изображений бумажного листка, расположенных, частью налагаясь одно на другое, в порядке преломляемости. От одновременного действия этих наложенных друг на друга цветных изображений глаз получает ощущение белого цвета (сложение спектральных цветов), но вверху и внизу выступают каемки несмешивающихся цветов. Знаменитый поэт Гёте, проделавший этот опыт и не понявший его смысла, вообразил, что он разоблачил таким образом ложность учения Ньютона о цветах, и написал затем собственную «Науку о цветах», которая почти всецело основана на превратных представлениях. Читатель, надо полагать, не повторит заблуждения великого поэта и не будет ожидать, что призма перекрасит для него все предметы. Земная атмосфера является для наших глаз как бы огромной воздушной призмой, обращенной основанием вниз. Глядя на Солнце у горизонта, мы смотрим на него сквозь газовую призму. Диск Солнца получает вверху каемку синего и зеленого цвета, внизу - красно-желтую. Пока Солнце стоит выше горизонта, свет диска своей яркостью перебивает гораздо менее яркие цветные полоски, и мы их не замечаем вовсе. Но в моменты восхода и захода Солнца, когда почти весь его диск скрыт под горизонтом, мы можем видеть синюю кайму верхнего края. Она двухцветная: выше расположена синяя полоска, ниже - голубая, от смешения синих и зеленых лучей. Когда воздух близ горизонта совершенно чист и прозрачен, мы видим синюю кайму - «синий луч». Но чаще синие лучи рассеиваются атмосферой и остается одна зеленая кайма: явление «зеленого луча». Наконец, в большинстве случаев рассеиваются мутной атмосферой также синие и зеленые лучи - тогда не замечается никакой каемки: Солнце закатывается багровым шаром.
Пулковский астроном Г. А. Тихов, посвятивший «зеленому лучу» специальное исследование, сообщает некоторые приметы видимости этого явления. «Если Солнце имеет при закате красный цвет и на него легко смотреть простым глазом, то можно с уверенностью сказать, что зеленого луча не будет». Причина понятна: красный цвет солнечного диска указывает на сильное рассеяние атмосферой синих и зеленых лучей, т. е. всей верхней каемки диска. «Наоборот, - продолжает астроном, - если Солнце мало изменило свой обычный беловато-желтый цвет и заходит очень ярким (т. е. если поглощение света атмосферой невелико. - Я. П. ), то можно с большой вероятностью ожидать зеленого луча. Но тут как раз важно, чтобы горизонт представлял резкую линию, без всяких неровностей, близкого леса, построек и т. п. Эти условия всего лучше выполняются на море; вот почему зеленый луч так хорошо известен морякам».
Итак, чтобы увидеть «зеленый луч», нужно наблюдать Солнце в момент заката или восхода при очень чистом небе. В южных странах небо у горизонта прозрачнее, чем у нас, поэтому явление «зеленого луча» наблюдается там чаще. Но и у нас оно не так редко, как думают многие, вероятно под влиянием романа Жюля Верна. Настойчивые поиски «зеленого луча» рано или поздно вознаграждаются успехом. Случалось улавливать это красивое явление даже в зрительную трубу. Два эльзасских астронома так описывают подобное наблюдение:
«…В последнюю минуту, предшествующую заходу Солнца, когда, следовательно, еще видна заметная часть его, диск, имеющий волнообразную движущуюся, но резко очерченную границу, окружен зеленым ободком. Пока Солнце не зашло окончательно, этот ободок не виден простым глазом. Он становится виден лишь в момент полного исчезновения Солнца за горизонтом. Если же смотреть в зрительную трубу с достаточно сильным увеличением (примерно в 100 раз), можно проследить подробно все явления: зеленая кайма становится заметной самое позднее за 10 минут до захода Солнца; она ограничивает верхнюю часть диска, тогда как от нижней наблюдается красная кайма. Ширина каймы, вначале очень малая (всего несколько секунд дуги), возрастает по мере захождения Солнца; она достигает иногда до полуминуты дуги. Над зеленым ободком часто наблюдаются зеленые же выступы, которые при постепенном исчезновении Солнца как бы скользят по его краю до высшей точки; иногда они отрываются от ободка и светятся несколько секунд отдельно, пока не погаснут» (рис. 119).

Рис. 119. Длительное наблюдение «зеленого луча»; наблюдатель видел «зеленый луч» за горным хребтом в течение 5 минут. Выше справа - «зеленый луч», видимый в подзорную трубу. Диск Солнца имеет неправильные контуры. В положении 1 блеск солнечного диска ослепляет глаз и мешает видеть зеленую каемку простым глазом. В положении 2, когда диск Солнца почти исчезает, «зеленый луч» становится доступным простому глазу.
Обычно явление длится секунду-две. Но при исключительной обстановке продолжительность его заметно удлиняется. Отмечен случай, когда «зеленый луч» наблюдался более 5 минут! Солнце садилось за отдаленной горой, и быстро шагавший наблюдатель видел зеленую кайму солнечного диска, словно скользящего по склону горы (рис. 119).
Очень поучительны случаи наблюдения «зеленого луча» при восходе Солнца, когда верхний край светила начинает показываться из-под горизонта. Это опровергает часто высказываемую догадку, будто «зеленый луч» - оптический обман, которому поддается глаз, утомленный ярким блеском только что закатившегося Солнца.
Солнце - не единственное светило, посылающее «зеленый луч». Случалось видеть это явление, порождаемое заходящей Венерой [О миражах и зеленом луче можно узнать из превосходной книги М. Миннарта «Свет и цвет в природе». Физматгиз, 1958 г. Прим. ред. ].




