Сила взаимодействия между зарядами формула. Взаимодействие зарядов. Закон Кулона

§ 2. Взаимодействие зарядов. Закон Кулона

Электрические заряды взаимодействуют между собой, т. е. одноименные заряды взаимно отталкиваются, а разноименные притягиваются. Силы взаимодействия электрических зарядов определяются законом Кулона и направлены по прямой линии, соединяющей точки, в которых сосредоточены заряды.
Согласно закону Кулона, сила взаимодействия двух точечных электрических зарядов прямо пропорциональна произведению количеств электричества в этих зарядах, обратно пропорциональна квадрату расстояния между ними и зависит от среды, в которой находятся заряды:

где F - сила взаимодействия зарядов, н (ньютон);
Один ньютон содержит ≈ 102 г силы.
q 1 , q 2 - количество электричества каждого заряда, к (кулон);
Один кулон содержит 6,3 · 10 18 зарядов электрона.
r - расстояние между зарядами, м ;
ε а - абсолютная диэлектрическая проницаемость среды (материала); эта величина характеризует электрические свойства той среды, в которой находятся взаимодействующие заряды. В Международной системе единиц (СИ) ε а измеряется в (ф/м ). Абсолютная диэлектрическая проницаемость среды

где ε 0 - электрическая постоянная, равная абсолютной диэлектрической проницаемости вакуума (пустоты). Она равна 8,86 · 10 -12 ф/м .
Величина ε, показывающая, во сколько раз в данной среде электрические заряды взаимодействуют между собой слабее, чем в вакууме (табл. 1), называется диэлектрической проницаемостью . Величина ε есть отношение абсолютной диэлектрической проницаемости данного материала к диэлектрической проницаемости вакуума:

Для вакуума ε = 1. Диэлектрическая проницаемость воздуха практически близка к единице.

Таблица 1

Диэлектрическая проницаемость некоторых материалов

На основании закона Кулона можно сделать вывод, что большие электрические заряды взаимодействуют сильнее, чем малые. С увеличением расстояния между зарядами сила их взаимодействия значительно слабее. Так, с увеличением расстояния между зарядами в 6 раз уменьшается сила их взаимодействия в 36 раз. При сокращении расстояния между зарядами в 9 раз увеличивается сила их взаимодействия в 81 раз. Взаимодействие зарядов также зависит от материала, находящегося между зарядами.
Пример. Между электрическими зарядами Q 1 = 2 · 10 -6 к и Q 2 = 4,43 · 10 -6 к , расположенными на расстоянии 0,5 м , помещена слюда (ε = 6). Вычислить силу взаимодействия указанных зарядов.
Решение . Подставляя в формулу значения известных величин, получим:

Если в вакууме электрические заряды взаимодействуют с силой F в, то, поместив между этими зарядами, например, фарфор, их взаимодействие можно ослабить в 6,5 раз, т. е. в ε раз. Это значит, что сила взаимодействия между зарядами может быть определена как отношение

Пример. Одноименные электрические заряды взаимодействуют в вакууме с силой F в = 0,25 н . С какой силой будут отталкиваться два заряда, если пространство между ними заполнено бакелитом? Диэлектрическая проницаемость этого материала равна 5.
Решение . Сила взаимодействия электрических зарядов

Так как один ньютон ≈ 102 г силы, то 0,05 н составляет 5,1 г .

Тема 1.1 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ.

Раздел 1 ОСНОВЫ ЭЛЕКТРОДИНАМИКИ

1. Электризация тел. Понятие о величине заряда.

Закон сохранения заряда.

2. Силы взаимодействия между зарядами.

Закон Кулона.

3. Диэлектрическая проницаемость среды.

4. Международная система единиц в электричестве.

1. Электризация тел. Понятие о величине заряда.

Закон сохранения заряда.

Если две поверхности привести в плотное соприкосновение, то возможен переход электронов с одной поверхности на другую, при этом на этих поверхностях появляются электрические заряды.

Это явление называется ЭЛЕКТРИЗАЦИЕЙ. При трении площадь плотного соприкосновения поверхностей увеличивается, увеличивается и величина заряда на поверхности – такое явление называют ЭЛЕКТРИЗАЦИЕЙ ТРЕНИЕМ.

В процессе электризации происходит перераспределение зарядов, в результате которого обе поверхности заряжаются равными по величине, противоположными по знаку зарядами.

Т.к. все электроны имеют одинаковые заряды (отриц.) е = 1,6 10Кл, то для того, чтобы определить величину заряда на поверхности (q), необходимо знать, сколько электронов в избытке или недостатке на поверхности (N) и заряд одного электрона.

В процессе электризации новые заряды не появляются и не исчезают, а только происходит их перераспределение между телами или частями тела, поэтому суммарный заряд замкнутой системы тел остается постоянным, в этом и заключается смысл ЗАКОНА СОХРАНЕНИЯ ЗАРЯДА.

2. Силы взаимодействия между зарядами.

Закон Кулона.

Электрические заряды взаимодействуют между собой, находясь на расстоянии, при этом одноименные заряды отталкиваются, а разноименные – притягиваются.

Впервые выяснил опытным путем отчего зависит сила взаимодействия между зарядами французский ученый Кулон и вывел закон, названный законом КУЛОНА. Закон фундаментальный т.е. основан на опытах. При выводе этого закона Кулон использовал крутильные весы.

3) k – коэффициент, выражающий зависимость от окружающей среды.

Формула закона Кулона.

Сила взаимодействия между двумя неподвижными точечными зарядами прямо пропорциональны произведению величин этих зарядов и обратно пропорциональна квадрату расстояний между ними, и зависит от среды, в которой находятся эти заряды, и направлена вдоль прямой, соединяющей центры этих зарядов.

3. Диэлектрическая проницаемость среды.

Е - диэлектрическая проницаемость среды, зависит от окружающей заряды среды.

Е = 8,85*10 - физическая постоянная, диэлектрическая проницаемость вакуума.

Е – относительная диэлектрическая проницаемость среды, показывает во сколько раз сила взаимодействия между точечными зарядами в вакууме больше чем в данной среде. В вакууме самое сильное взаимодействие между зарядами.

4. Международная система единиц в электричестве.

Основной единицей для электричества в системе «СИ» является сила тока в 1А, все остальные единицы измерения являются производными от 1Ампера.

1Кл – количество электрического заряда, переносимого заряженными частицами через поперечное сечение проводника при силе тока в 1А за 1с.

q=N;

Тема 1.2 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

1. Электрическое поле – как особый вид материи.

2. Напряженность электрического поля.

6. Связь разности потенциалов с напряженностью электрического поля.

1. Электрическое поле – как особый вид материи.

В природе как вид материи существует электромагнитное поле. В разных случаях электромагнитное поле проявляет себя по - разному, так например около неподвижных зарядов проявляет себя только электрическое поле, которое называют электростатическим. Около подвижных зарядов можно обнаружить как электрическое, так и магнитное поля, которые в совокупности представляют ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ.

Рассмотрим свойства электростатических полей:

1) Электростатическое поле создается неподвижными зарядами, обнаружить такие поля можно

с помощью пробных зарядов (небольшой по величине положительный заряд), т.к. только на них электрическое поле оказывает силовое действие, которое подчиняется закону Кулона.

2. Напряженность электрического поля.

Эл.поле как вид материи обладает энергией, массой, распространяется в пространстве с конечной скоростью и теоретических границ не имеет.

Практически считается, что поля нет если оно не оказывает заметного действия на пробные заряды.

Так как обнаружить поле можно с помощью силового действия на пробные заряды, то основной характеристикой электрического поля является напряженность.

Если в одну и ту же точку электрического поля вносить разные по величине пробные заряды, то между действующей силой и величиной пробного заряда прямая пропорциональная зависимость.

Коэффициентом пропорциональности между действующей силой и величиной заряда является напряженность Е.

Е = -формула расчета напряженности электрического поля, если q = 1 Кл, то | E | = | F |

Напряженность является силовой характеристикой точек электрического поля, т.к. она численно равна силе, действующей на заряд в 1 Кл в данной точке электрического поля.

Напряженность – величина векторная, вектор напряженности по направлению совпадает с вектором силы, действующей на положительный заряд в данной точке электрического поля.

3. Линии напряженности электрического поля. Однородное электрическое поле.

Для того, чтобы наглядно можно было изображать электрическое поле, т.е. графически, используют линии напряженности электрического поля. Это такие линии, иначе называемые силовыми линиями, касательные к которым по направлению совпадают с векторами напряженности в точках электрического поля через которые эти линии проходят,

Линии напряженности обладают следующими свойствами:

1) Начинаются на полож. зарядах, заканчиваются – на отрицательных, или начинаются на положител. зарядах и уходят в бесконечность, или приходят из бесконечности и заканчиваются на положительных зарядах..

2) Эти линии непрерывны и нигде не пересекаются.

3) Густота линий (кол-во линий на единицу площади поверхности) и напряженность электрического поля находятся в прямой и пропорциональной зависимости.

В однородном электрическом поле напряженность во всех точках поля одинакова, графически такие поля изображаются параллельными линиями на равном расстоянии друг от друга. Такое поле можно получить между двумя параллельными плоскими заряженными пластинами на маленьком расстоянии друг от друга.

4. Работа по перемещению заряда в электрическом поле.

Поместим в однородное электрическое поле электрический заряд. Со стороны поля на заряд будут действовать силы. Если заряд перемещать, то может совершаться работа.

Совершенная работа на участках:

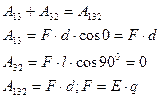
А = q E d - формула расчета работы по перемещению заряда в электрическом поле.

Вывод: Работа по перемещению заряда в электрическом поле от формы траектории не зависит, а она зависит от величины перемещаемого заряда (q) , напряженности поля (Е), а также от выбора начальной и конечной точек перемещения (d).

Если заряд в электрическом поле перемещать по замкнутому контуру, то совершаемая работа будет равна 0. Такие поля называются потенциальными полями. Тела в таких полях обладают потенциальной энергией, т.о. электрический заряд в любой точке электрического поля обладает энергией и совершаемая работа в электрическом поле равна разности потенциальных энергий заряда в начальной и конечной точках перемещения.

5. Потенциал. Разность потенциалов. Напряжение.

Если в данную точку электрического поля помещать разные по величине заряды, то потенциальная энергия заряда и его величина находятся в прямой пропорциональной зависимости.

-(фи) потенциал точки электрического поля

примем

Потенциал является энергетической характеристикой точек электрического поля, т.к. он численно равен потенциальной энергии заряда в 1 Кл в данной точке электрического поля.

На равных расстояниях от точечного заряда потенциалы точек поля одинаковы. Эти точки образуют поверхность равного потенциала, и такие поверхности называются эквипотенциальными поверхностями. На плоскости это окружности, в пространстве – это сферы.

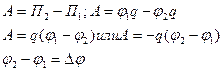
Напряжение

Формулы расчета работы по перемещению заряда в электрическом поле.

1В – напряжение между точками электрического поля при перемещении в которых заряда в 1Кл совершается работа в 1 Дж.

- формула, устанавливающая связь между напряженностью электрического поля, напряжением и разностью потенциалов.

Напряженность численно равна напряжению или разности потенциалов между двумя точками поля взятыми вдоль одной силовой линии на расстоянии 1м. Знак (-) означает, что вектор напряженности всегда направлен в сторону точек поля с уменьшающимся потенциалом.

Известно, что каждое заряженное тело имеет электрическое поле. Можно также утверждать, что если есть электрическое по-ле, то есть заряженное тело, которому при-надлежит это поле. Итак, если рядом нахо-дятся два заряженных тела с электриче-скими зарядами, то можно сказать, что каж-дое из них находится в электрическом поле соседнего тела. А в таком случае на первое тело будет действовать сила

F 1 = q 1 E 2 ,

где q 1 — заряд первого тела; E 2 — напря-женность поля второго тела. На второе те-ло, соответственно, будет действовать сила

F 2 = q 2 E 1 ,

где q 2 — заряд первого тела; E 1 — напря-женность поля второго тела.

Электрически заряженное те-ло взаимодействует с элект-рическим полем другого заря-женного тела.

Если эти тела небольшие (точечные), то

E 1 = k . q 1 / r 2 ,

E 2 = k . q 2 / r 2 ,

Силы, действующие на каждое из взаимодействующих заря-женных тел, можно рассчи-тать, зная лишь их заряды и расстояние между ними.

Подставим значения напряженности и получим

F 1 = k . q 1 q 2 / r 2 и F 2 = k . q 2 q 1 / r 2 .

Значение каждой силы выражается лишь через значение зарядов каждого тела и рас-стояние между ними. Таким образом, опре-делять силы, действующие на каждое тело, можно, пользуясь лишь знаниями об элект-рических зарядах тел и расстоянии между ними. На этом основании можно сформу-лировать один из фундаментальных законов электродинамики — закона Кулона .

Закон Кулона . Сила, действующая на неподвижное то-чечное тело с электрическим зарядом в поле другого неподвижного точечного тела с элект-рическим зарядом, пропорциональна произве-дению значений их зарядов и обратно пропор-циональна квадрату расстояния между ними.

В общем виде значение силы, о которой идет речь в формулировке закона Кулона , можно записать так:

F = k . q 1 q 2 / r 2 ,

В формуле для расчета силы взаимодей-ствия записаны значения зарядов обоих тел. Поэтому можно сделать вывод, что по мо-дулю обе силы равны. Тем не менее, по направлению — они противоположные. В слу-чае если заряды тел одноименные, тела от-талкиваются (рис. 4.48). Если заряды тел раз-ноименные, то тела притягиваются (рис. 4.49). Окончательно можно записать:

F̅ 1 = - F̅ 2 .

Записанное равенство подтверждает спра-ведливость III закона динамики Ньютона для электрических взаимодействий. Поэтому в одной из распространенных формулиро-вок закона Кулона говорится, что

сила взаи-модействия двух заряженных точечных тел пропорциональна произведению значений их за-рядов и обратно пропорциональна квадрату расстояния между ними.

Если заряженные тела находятся в ди-электрике, то сила взаимодействия будет зависеть от диэлектрической проницаемости этого диэлектрика

F = k . q 1 q 2 / ε r 2 .

Для удобства расчетов, базирующихся на законе Кулона, значение коэффициента k записывают иначе:

k = 1 / 4 πε 0 .

Величина ε 0 называется электрической по-стоянной . Ее значение вычисляется в соот-ветствии с определением:

9 . 10 9 Н.м 2 /Кл 2 = 1 / 4πε 0 ,

ε 0 = (1 / 4π) . 9 . 10 9 Н.м 2 /Кл 2 = 8,85 . 10 -12 Кл 2 /Н.м 2 . Материал с сайта

Таким образом, закон Кулона в общем случае можно выразить формулой

F = (1 / 4πε 0 ) . q 1 q 2 / ε r 2 .

Закон Кулона является одним из фунда-ментальных законов природы. На нем бази-руется вся электродинамика, и не отмечено ни единого случая, когда бы нарушался закон Кулона . Существует единственное ог-раничение, которое касается действия за-кона Кулона на различных расстояниях. Счи-тается, что закон Кулона действует на рас-стояниях больше 10 -16 м и меньше несколь-ких километров.

При решении задач необходимо учиты-вать, что закон Кулона касается сил вза-имодействия точечных неподвижных заря-женных тел. Это сводит все задачи к задачам о взаимодействии неподвижных заряженных тел, в которых применяется два положения статики:

1. равнодействующая всех сил, действую-щих на тело, равна нулю;
2. сумма моментов сил равна нулю.

В подавляющем большинстве задач на применение закона Кулона достаточно учи-тывать лишь первое положение.

На этой странице материал по темам:

• Доклад по физике закон кулона

• Закон кулона что означают формулы

• Реферат на тему закон кулона по физике