Магнитный момент равен. Магнитный момент - большая советская энциклопедия

Данная страница пока только на русском языке.

1. Магнетизм

2. Магнитное поле

3. Постоянный магнит

1. Магнетизм - форма взаимодействия движущихся электрических зарядов, осуществляемая на расстоянии посредством магнитного поля. , атомов и молекул, а в макроскопическом масштабе - электрический ток и постоянные магниты. Наряду с электричеством, магнетизм - одно из проявлений электромагнитного взаимодействия. Основной характеристикой магнитного поля является вектор индукции, совпадающий в вакууме с вектором напряженности магнитного поля.

Магнитный момент, магнитный дипольный момент - основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента - спина. Магнитный момент измеряется в А*м2 или Дж/Тл (СИ).

Формулы для вычисления магнитного момента
В случае плоского контура с электрическим током магнитный момент вычисляется как
, где I - сила тока в контуре, S - площадь контура, n - единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

где r - радиус-вектор проведенный из начала координат до элемента длины контура dl

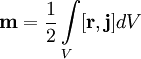
где j - плотность тока в элементе объёма dV.

2. Магнитное поле - составляющая электромагнитного поля, появляющаяся при наличии изменяющегося во времени электрического поля. Кроме того, магнитное поле может создаваться током заряженных частиц, либо магнитными моментами электронов в атомах (постоянные магниты). Основной характеристикой магнитного поля является его сила, определяемая вектором магнитной индукции B . В СИ магнитная индукция измеряется в Тесла (Тл).

Магнитное поле - это особый вид материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.

Можно также рассматривать магнитное поле, как релятивистскую составляющую электрического поля. Точнее, магнитные поля являются необходимым следствием существования электрических полей и специальной теории относительности. Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются свет и прочие электромагнитных волны.

Проявление магнитного поля
Магнитное поле проявляется в воздействии на магнитные моменты частиц и тел, на движущиеся заряженные частицы (или проводники с током). Сила, действующая на движущуюся в магнитном поле электрически заряженную частицу, называется силой Лоренца, которая всегда направлена перпендикулярно к вектору v

где a - угол между направлением вектора скорости частицы v v и направлением вектора магнитного поля B

Также магнитное поле действует на проводник с током. Сила, действующая на проводник будет называться силой Ампера. Эта сила складывается из сил, действущих на отдельные движущиеся внутри проводника заряды.

Взаимодействие двух магнитов
Наиболее часто встречаемое проявление магнитного поля - взаимодействие двух магнитов: подобные полюса отталкиваются, противоположные притягиваются. Представляется заманчивым описать взаимодействие между магнитами, как взаимодействие между двумя монополями, но эта идея не приводит к правильному описанию явления.

Правильнее будет сказать, что на магнитный диполь помещённый в неоднородное поле действует сила, которая стремится повернуть его так, чтобы магнитный момент диполя был сонаправлен с магнитным полем.

Сила, действующая на магнитный диполь с магнитным моментом m выражается по формуле:

Сила, действующую на магнит со стороны неоднородного магнитного поля, может быть также определенна суммированием всех сил, действующих на элементарные диполи, составляющие магнит.

Энергию магнитного поля можно найти по формуле:

где: Ф - магнитный поток, I - ток, L - индуктивность катушки или витка с током.

3. Постоянный магнит - изделие различной формы из жёсткого материала с высокой остаточной магнитной индукцией, сохраняющие состояние намагниченности в течение длительного времени. Постоянные магниты применяются в качестве автономных (не потребляющих энергии) источников магнитного поля.

Свойства магнита определяются характеристиками размагничивающего участка петли магнитного гистерезиса материала магнита: чем выше остаточная индукция Br и коэрцитивная сила Hc, тем выше намагниченность и стабильность магнита.

Индукция постоянного магнита Bd не может превышать Br: равенство Bd = Br возможно лишь в том случае, если магнит представляет собой замкнутый магнитопровод, то есть не имеет воздушного промежутка, однако постоянные магниты, как правило, используются для создания магнитного поля в воздушном (или заполненном другой средой) зазоре, в этом случае Bd
Для производства постоянных магнитов используются четыре основных класса материалов:

керамические (ферриты)


неодим-железо-бор (Nd-Fe-B, NdFeB, NIB)


самарий-кобальт (SmCo)


альнико (Alnico)

Наиболее широко распространены ферритовые магниты.

Для применений при обычных температурах самые сильные постоянные магниты делаются из сплавов, содержащих неодим. Они используются в таких областях, как магнитно-резонансная томография, сервоприводы жёстких дисков и создание высококачественных динамиков.

Постоянные магниты на уроках физики обычно демонстрируются в виде подковы, полюса которой окрашены в синий и красный цвет.

Отдельные шарики и цилиндры с сильными магнитными свойствами используются в качестве хай-тек украшений/игрушек - они без дополнительных креплений собираются в цепочки, которые можно носить как браслет. Так же в продаже есть конструкторы, состоящие из набора цилиндрических магнитных палочек и стальных шариков. Из них можно собирать множество конструкций, в основном фермового типа.

Кроме того, существуют гибкие плоские магниты на полимерной основе с магнитными добавками, которые используются например, для изготовления декоративных магнитов на холодильники, оформительских и прочих работ. Выпускаются в виде лент и листов, обычно с нанесённым клеевым слоем и плёнкой, его защищающей. Магнитное поле у такого плоского магнита полосатое - с шагом около двух миллиметров по всей поверхности чередуются положительные и отрицательные полюса.

Сила притяжения постоянного магнита (или мощность постоянного магнита) зависит от множества параметров таких как:

линейные размеры самого магнита


намагниченность и материал изготовления магнита


отдаленность или площадь соприкосновения с притягивающимся предметом


линейные размеры притягивающегося предмета, включая толщину

Известно, что магнитное поле оказывает ориентирующее действие на рамку с током, и рамка поворачивается вокруг своей оси. Происходит это потому, что в магнитном поле на рамку действует момент сил, равный:

М = I S |B → | sin α.

Здесь B → - вектор индукции магнитного поля, I - ток в рамке, S - ее площадь и α - угол между силовыми линиями и перпендикуляром к плоскости рамки. В это выражение входит произведение I S которое называют магнитным дипольным моментом или просто магнитным моментом рамки Оказывается, величина магнитного момента полностью характеризует взаимодействие рамки с магнитным полем. Две рамки, у одной из которых большой ток и малая площадь, а у другой - большая площадь и малый ток, будут вести себя в магнитном поле одинаково, если их магнитные моменты равны. Если рамка маленькая, то ее взаимодействие с магнитным полем не зависит от ее формы.

Удобно считать магнитный момент вектором, который расположен на линии, перпендикулярной плоскости рамки. Направление вектора (вверх или вниз вдоль этой линии) определяется «правилом буравчика»: буравчик нужно расположить перпендикулярно плоскости рамки и вращать по направлению тока рамки - направление движения буравчика укажет направление вектора магнитного момента.

Таким образом, магнитный момент - это вектор I S, перпендикулярный плоскости рамки.

Теперь наглядно представим поведение рамки в магнитном поле. Она будет стремиться развернуться так. чтобы ее магнитный момент был направлен вдоль вектора индукции магнитного поля B →

Магнитный момент - важное понятие в физике. В состав атомов входят ядра, вокруг которых вращаются электроны. Каждый движущийся вокруг ядра электрон как заряженная частица создает ток, образуя как бы микроскопическую рамку с током. Вычислим магнитный момент одного электрона, движущегося по круговой орбите радиуса r.

Электрический ток, т. е. величина заряда, которая переносится электроном на орбите за 1 с, равна заряду электрона е, помноженному на число совершаемых им оборотов v/2πr:

Следовательно, величина магнитного момента электрона равна:

μ = I S=ev/(2πr) (πr 2) = evr/2.

μ можно выразить через величину момента импульса электрона L=m v r. Тогда величина магнитного момента электрона, связанная с его движением по орбите, или, как говорят, величина орбитального магнитного момента, равна:

Атом - это объект, который нельзя описать с помощью классической физики: для таких малых объектов действуют совершенно иные законы - законы квантовой механики. Тем не менее результат, полученный для орбитального магнитного момента электрона, оказывается таким же, как и в квантовой механике. Иначе дело обстоит с собственным магнитным моментом электрона - спином, который связан с его вращением вокруг своей оси. Для спина электрона квантовая механика дает величину магнитного момента, в 2 раза большую, чем классическая физика:

и это различие между орбитальным и спиновым магнитными моментами невозможно объяснить с классической точки зрения. Полный магнитный момент атома складывается из орбитальных и спиновых магнитных моментов всех электронов, а поскольку они отличаются в 2 раза, то в выражении для магнитного момента атома появляется множитель g(1

Таким образом, атом, как и обычная рамка с током, обладает магнитным моментом, и во многом их поведение сходно. В частности, как и в случае классической рамки, поведение атома в магнитном поле полностью определяется величиной его магнитного момента. В связи с этим понятие магнитного момента очень важно при объяснении различных физических явлений, происходящих с веществом в магнитном поле.

Характеризующая магнитные свойства любых веществ. Источником формирования магнетизма, как утверждает классическая электромагнитная теория, являются микротоки, возникающие вследствие движения электрона по орбите. Магнитный момент - это непременное свойство всех без исключения ядер, атомных электронных оболочек и молекул.

Магнетизм, который присущ всем элементарным частицам, согласно обусловлен наличием у них механического момента, называемого спином (собственным механическим импульсом квантовой природы). Магнитные свойства атомного ядра складываются из спиновых импульсов составных частей ядра - протонов и нейтронов. Электронные оболочки (внутриатомные орбиты) тоже имеют магнитный момент, который составляет сумма магнитных моментов находящихся на ней электронов.

Иначе говоря, магнитные моменты элементарных частиц и обусловлены внутриатомным квантомеханическим эффектом, известным как спиновой импульс. Данный эффект аналогичен угловому моменту вращения вокруг собственной центральной оси. Спиновой импульс измеряется в постоянной Планка - основной константе квантовой теории.

Все нейтроны, электроны и протоны, из которых, собственно, и состоит атом, согласно Планку, обладают спином, равным ½ . В структуре атома электроны, вращаясь вокруг ядра, помимо спинового импульса, имеют еще и орбитальный угловой момент. Ядро, хоть и занимает статичное положение, тоже обладает угловым моментом, который создается эффектом ядерного спина.

Магнитное поле, которое генерирует атомный магнитный момент, определяется различными формами этого углового момента. Наиболее заметный вклад в создание вносит именно спиновой эффект. По согласно которому два тождественных электрона не могут пребывать одновременно в одинаковом квантовом состоянии, связанные электроны сливаются, при этом их спиновые импульсы приобретают диаметрально противоположные проекции. В этом случае магнитный момент электрона сокращается, что уменьшает магнитные свойства всей структуры. В некоторых элементах, имеющих четное число электронов, этот момент уменьшается до нулевой отметки, и вещества перестают обладать магнитными свойствами. Таким образом, магнитный момент отдельных элементарных частиц оказывает непосредственное влияние на магнитные качества всей ядерно-атомной системы.

Ферромагнитные элементы с нечетным количеством электронов всегда будут обладать ненулевым магнетизмом за счет непарного электрона. В таких элементах соседние орбитали перекрываются, и все спиновые моменты непарных электронов принимают одинаковую ориентацию в пространстве, что приводит к достижению наименьшего энергетического состояния. Этот процесс называется обменным взаимодействием.

При таком выравнивании магнитных моментов ферромагнитных атомов возникает магнитное поле. А парамагнитные элементы, состоящие из атомов с дезориентированными магнитными моментами, не имеют собственного магнитного поля. Но если воздействовать на них внешним источником магнетизма, то магнитные моменты атомов выровняются, и эти элементы тоже приобретут магнитные свойства.

Орбитальный М. м. электрона mорб связан с механическим орбитальным моментом орб соотношением g opб = |mорб| / | орб| = |e |/2m ec , то есть магнитомеханическое отношение gopб в два раза меньше, чем g cп. Квантовая механика допускает лишь дискретный ряд возможных проекций mорб на направление внешнего поля (так называемое квантование пространственное): mНорб = mlmв, где ml -магнитное квантовое число, принимающее 2l + 1 значений (0, ±1, ±2,..., ±l , где l -орбитальное квантовое число). В многоэлектронных атомах орбитальный и спиновый М. м. определяются квантовыми числами L и S суммарного орбитального и спинового моментов. Сложение этих моментов проводится по правилам пространственного квантования. В силу неравенства магнитомеханических отношений для спина электрона и его орбитального движения (g cп ¹ g opб) результирующий М. м. оболочки атома не будет параллелен или антипараллелен её результирующему механическому моменту J .Поэтому часто рассматривают слагающую полного М. м. на направление вектора J , равную

где g J - магнитомеханическое отношение электронной оболочки, J - полное угловое квантовое число.

М. м. протона, спин которого равен

должен был бы по аналогии с электроном равняться

где Mp - масса протона, которая в 1836,5 раз больше m e, mяд - ядерный магнетон, равный 1/1836,5mв. У нейтрона же М. м. должен был бы отсутствовать, поскольку он лишён заряда. Однако опыт показал, что М. м. протона mp = 2,7927mяд, а нейтрона mn = -1,91315mяд. Это обусловлено наличием мезонных полей около нуклонов, определяющих их специфические ядерные взаимодействия (см. Ядерные силы , Мезоны) и влияющих на их электромагнитные свойства. Суммарные М. м. сложных атомных ядер не являются кратными mяд или mp и mn. Таким образом, М. м. ядра калия равен -1,29 mяд. Причиной этой неаддитивности является влияние ядерных сил, действующих между образующими ядро нуклонами. М. м. атома в целом равен векторной сумме М. м. электронной оболочки и атомного ядра.

Для характеристики магнитного состояния макроскопических тел вычисляется среднее значение результирующего М. м. всех образующих тело микрочастиц. Отнесённый к единице объёма тела М. м. называется намагниченностью. Для макротел, особенно в случае тел с атомным магнитным упорядочением (ферро-, ферри- и антиферромагнетики), вводят понятие средних атомных М. м. как среднего значения М. м., приходящегося на один атом (ион) - носитель М. м. в теле. В веществах с магнитным порядком эти средние атомные М. м. получаются как частное от деления самопроизвольной намагниченности ферромагнитных тел или магнитных подрешёток в ферри- и антиферромагнетиках (при абсолютном нуле температуры) на число атомов - носителей М. м. в единице объёма. Обычно эти средние атомные М. м. отличаются от М. м. изолированных атомов; их значения в магнетонах Бора mв оказываются дробными (например, в переходных d-металлах Fe, Со и Ni соответственно 2,218 mв, 1,715 mв и 0,604 mв) Это различие обусловлено изменением движения d-электронов (носителей М. м.) в кристалле по сравнению с движением в изолированных атомах. В случае редкоземельных металлов (лантанидов), а также неметаллических ферро- или ферримагнитных соединений (например, ферриты) недостроенные d- или f-слои электронной оболочки (основные атомные носители М. м.) соседних ионов в кристалле перекрываются слабо, поэтому заметной коллективизации этих слоев (как в d-металлах) нет и М. м. таких тел изменяются мало по сравнению с изолированными атомами. Непосредственное опытное определение М. м. на атомах в кристалле стало возможным в результате применения методов магнитной нейтронографии, радиоспектроскопии (ЯМР, ЭПР, ФМР и т.п.) и Мёссбауэра эффекта. Для парамагнетиков также можно ввести понятие среднего атомного М. м., который определяется через найденную на опыте постоянную Кюри, входящую в выражение для Кюри закона или Кюри - Вейса закона (см. Парамагнетизм).

Лит.: Тамм И. Е., Основы теории электричества, 8 изд., М., 1966; Ландау Л. Д. и Лифшиц Е. М., Электродинамика сплошных сред, М., 1959; Дорфман Я. Г., Магнитные свойства и строение вещества, М., 1955; Вонсовский С. В., Магнетизм микрочастиц, М., 1973.

С. В. Вонсовский.