Произведение давления на объем. Закон Бойля-Мариотта. Газовые законы. Изотерма

Изучение зависимости между параметрами, характеризующими состояние данной массы газа, начнем с изучения газовых процессов, протекающих при неизменности одного из параметров. Английский ученый Бойль (в 1669 г.) и французский ученый Мариотт (в 1676 г.) открыли закон, который выражает зависимость изменения давления от изменения объема газа при постоянной температуре. Проведем следующий опыт.

Вращением рукоятки будем изменять объем газа (воздуха) в цилиндре А (рис. 11, а). По показанию манометра заметим что и давление газа при этом изменяется. Будем менять объем газа в сосуде (объем определяется по шкале В) и, замечая давление, запишем их в табл. 1. Из нее видно, что произведение объема газа на его давление было почти постоянным: во сколько раз "уменьшался объем газа, во столько же раз увеличивалось его давление.

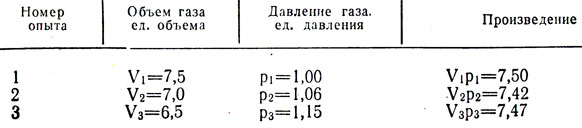
В результате подобных, более точных, опытов было открыто: для данной массы газа при постоянной температуре давление газа изменяется обратно пропорционально изменению объема газа. Это и есть формулировка закона Бойля-Мариотта. Математически он для двух состояний запишется так:

Процесс изменения состояния газа при постоянной температуре называется изотермическим. Формула закона Бойля-Мариотта является уравнением изотермического состояния газа. При постоянной температуре средняя скорость движения молекул не меняется. Изменение объема газа вызывает изменение числа ударов молекул о стенки сосуда. Это и есть причина изменения давления газа.

Изобразим графически этот процесс, например для случая V = 12 л, р = 1 ат. . Будем откладывать на оси абсцисс объем газа, а на оси ординат - его давление (рис. 11, б). Найдем точки, соответствующие каждой паре значений V и р, и, соединив их между собой, получим график изотермического процесса. Линия, изображающая зависимость между объемом и давлением газа При постоянной температуре, называется изотермой. Изотермические процессы в чистом виде не встречаются. Но нередки случаи, когда температура газа мало меняется, например при накачивании компрессором воздуха в баллоны, при впуске горючей смеси в цилиндр двигателя внутреннего сгорания. В таких случаях расчеты объема и давления газа производятся по закону Бойля- Мариотта * .

По своим механическим свойствам газы имеют много общего с жидкостями. Так же как и жидкости, они не обладают упругостью по отношению к изменениям формы. Отдельные части газа легко могут перемещаться друг относительно друга. Так же как и жидкости, они обладают упругостью относительно деформации всестороннего сжатия. При увеличении внешних давлений объем газа уменьшается. При снятии внешних давлений объем газа возвращается к первоначальному значению.

В существовании упругих свойств газа легко убедиться на опыте. Возьмите детский воздушный шар. Надуйте его не очень сильно и завяжите. После этого начните сдавливать его руками (рис. 3.20). При появлении внешних давлений шар сожмется, его объем уменьшится. Если прекратить сдавливание, шар сразу расправится, как будто у него внутри есть пружины.

Возьмите воздушный насос для автомашины или велосипеда, закройте его выходное отверстие и надавите на ручку поршня. Воздух, заключенный внутри насоса, начнет сжиматься, и вы сразу почувствуете быстрое нарастание давления. Еслн перестать давить на поршень, он вернется на место, и воздух займет первоначальный объем.

Упругость газа по отношению к всестороннему сжатию используется в шинах автомашин для амортизации, в воздушных тормозах и других устройствах. Первым упругие свойства газа, его способность изменять свой объем при изменении давления заметил Блез Паскаль.

Как мы уже отмечали, газ отличается от жидкости тем, что не может сам по себе сохранять объем неизменным и не имеет свободной поверхности. Он обязательно должен находиться в замкнутом сосуде и всегда будет полностью занимать весь объем этого сосуда.

Другим важным отличием газа от жидкости является его большая сжимаемость (податливость). Уже при очень малых изменениях давления возникают хорошо заметные большие изменения объема газа. Кроме того, связь между давлениями и изменениями объема для газа носит более сложный характер, чем для жидкости. Изменения объема уже не будут прямо пропорциональны изменениям давления.

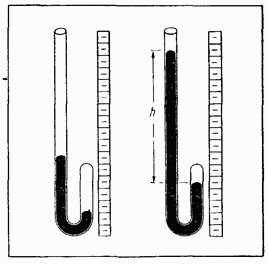
Впервые количественную связь между давлением и объемом газа установил английский ученый Роберт Бойль (1627-1691). В своих опытах Бойль наблюдал за изменениями объема воздуха, заключенного в запаянном конце трубки (рис. 3.21). Давление на этот воздух он изменял, подливая ртуть в длинное колено трубки. Давление определялось по высоте столба ртути

Опыт Бойля в приближенном, грубом виде вы можете повторить с воздушным насосом. Возьмите хороший насос (важно, чтобы поршень не пропускал воздух), закройте выходное отверстие и нагружайте поочередно ручку поршня одним, двумя, тремя одинаковыми грузами. Одновременно отмечайте положения ручки при разных нагрузках относительно вертикальной линейки.

Даже такой грубый опыт позволит вам убедиться в том, что объем данной массы газа обратно пропорционален давлению, которому подвергается этот газ. Независимо от Бойля такие же опыты ставил французский ученый Эдмон Мариотт (1620-1684), который пришел к таким же результатам, как и Бойль.

Одновременно Мариотт обнаружил, что при проведении опыта нужно соблюдать одну очень важную предосторожность: температура газа во время опыта должна оставаться постоянной, иначе результаты опыта будут другими. Поэтому закон Бойля - Мариотта читается так; при постоянной температуре объем данной массы газа обратно пропорционален давлению.

Если обозначить через начальные объем и давление газа, через конечные объем и давление той же массы газа, то

закон Бойля - Мариотта можно записать в виде следующей формулы:

Представим закон Бойля - Мариотта в наглядной графической форме. Для определенности допустим, что некоторая масса газа занимала объем при давлении Изобразим графически, как будет меняться объем этого газа с увеличением давления при постоянной температуре. Для этого рассчитаем объемы газа по закону Бойля - Мариотта для давлений 1, 2, 3, 4 и т. д. атмосфер и составим таблицу:

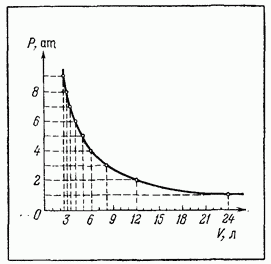
По этой таблице легко построить график зависимости давления газа от его объема (рис. 3.22).

Как видно из графика, зависимость давления от объема газа действительно носит сложный характер. Сначала увеличение давления от одной до двух единиц приводит к уменьшению объема в два раза. В дальнейшем при таких же приращениях давления возникают все более малые изменения начального объема. Чем больше сжимается газ, тем более упругим он становится. Поэтому для газа нельзя указать какого-нибудь постоянного модуля сжатия (характеризующего его упругие свойства), как это сделано для твердых тел. У газа модуль сжатия зависит от давления, под которым находится модуль сжатия растет вместе с давлением.

Заметим, что закон Бойля - Мариотта соблюдается только для не очень больших давлений и не очень низких температур. При высоких давлениях и низких температурах зависимость между объемом и давлением газа становится еще более сложной. Для воздуха, например, при 0°С закон Бойля - Мариотта дает правильные значения объема при давлении не выше 100 ат.

В начале параграфа уже говорилось, что упругие свойства газа, его большая сжимаемость широко используются человеком в практической деятельности. Приведем еще несколько примеров. Возможность сильно сжимать газ с помощью высоких давлений позволяет хранить большие массы газа в малых объемах. Баллоны со сжатым воздухом, водородом, кислородом широко используются в промышленности, например при газовой сварке (рис. 3.23).

Хорошие упругие свойства газа послужили основой для создания речных судов на воздушной подушке (рис. 3.24). Эти суда нового типа идоеют скорости, намного превосходящие те, которые удавалось получить раньше. Благодаря использованию упругих свойств воздуха удалось избавиться от больших сил трения. Правда, в этом случае расчет давления значительно усложняется, потому что приходится рассчитывать давления в быстрых потоках воздуха.

В основе многих биологических процессов также лежит использование упругих свойств воздуха. Задумывались ли вы, например, о том, как дышите? Что происходит при вдохе?

По сигналу нервной системы о том, что организму не хватает кислорода, человек при вдохе с помощью мышц грудной клетки поднимает ребра, с помощью других мышц опускает диафрагму. При этом увеличивается объем, который могут занять легкие (и находящиеся, в них остатки воздуха). Но такое увеличение объема приводит к большому уменьшению давления воздуха в легких. Возникает разность давлений между наружным воздухом и воздухом в легких. В результате наружный воздух начинает сам входить в легкие за счет своих упругих свойств.

Мы только предоставляем ему возможность войти, изменяя объем легких.

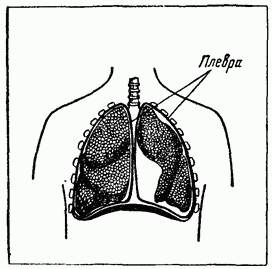
Не только в этом состоит использование упругости воздуха при дыхании. Легочная ткань очень нежная, и она не выдержала бы многократных растягиваний и довольно грубых нажимов грудных мышц. Поэтому она и не прикреплена к ним (рис. 3.25). Кроме этого, расширение легкого путем растягивания его поверхности (с помощью грудных мышц) вызвало бы неравномерное, неодинаковое расширение легкого в разных частях. Поэтому легкое окружено особой пленкой - плеврой. Плевра одной своей частью прикреплена к легкому, а другой - к мышечной ткани грудной клетки. Плевра образует своеобразный мешок, стенки которого не пропускают воздуха.

Внутри самой плевральной полости содержится очень небольшое количество газа. Давление этого газа становится равным давлению воздуха в легких только тогда, когда стенки плевры находятся очень близко друг от друга. При вдохе объем полости резко увеличивается. Давление в ней резко падает. Легкое за счет остатков содержащегося в нем воздуха начинает само расширяться равномерно во всех частях подобно резиновому шарику под колоколом воздушного насоса.

Таким образом, природа мудро использовала упругие свойства воздуха для создания идеального амортизатора для ткани легкого и самых выгодных условий для его расширения и сжатия.

При решении задач на применение законов Ньютона мы будем использовать закон Бойля - Мариотта как дополнительное уравнение, выражающее особые упругие свойства газов.

При постоянной температуре объем, занимаемый газом, обратно пропорционален его давлению.

Роберт Бойль — яркий пример ученого-джентльмена, сына давно ушедшей эпохи, когда наука была уделом исключительно состоятельных людей, посвящавших занятиям ею свой досуг. Большинство исследований Бойля относятся по современной классификации к разряду химических опытов, хотя сам себя он, наверняка, считал натурфилософом (физиком-теоретиком) и естествоиспытателем (физиком-экспериментатором). Судя по всему, поведением газов он заинтересовался, увидев проект одного из первых в мире воздушных насосов. Сконструировав и построив очередную, усовершенствованную версию своего двустороннего воздушно-вакуумного насоса, он решил исследовать, как повышенное и пониженное давление газа в герметичном сосуде, к которому был подключен его новый аппарат, влияет на свойства газов. Будучи одаренным экспериментатором, Бойль одновременно придерживался весьма новых и необычных для той эпохи взглядов, считая, что наука должна идти от эмпирических наблюдений, а не основываться исключительно на умозрительно-философских построениях.

В формулировке Бойля закон звучал буквально так: «Под воздействием внешней силы газ упруго сжимается, а в ее отсутствие расширяется, при этом линейное сжатие или расширение пропорционально силе упругости газа». Представьте, что вы сдавливаете надутый воздушный шарик. Поскольку свободного пространства между молекулами воздуха достаточно, вы без особого труда, приложив некоторую силу и проделав определенную работу, сожмете шарик, уменьшив объем газа внутри него. Это одно из основных отличий газа от жидкости. В шарике с жидкой водой, например, молекулы упакованы плотно, как если бы шарик был заполнен микроскопическими дробинками. Поэтому вода не поддается, в отличие от воздуха, упругому сжатию. (Если не верите, попробуйте протолкнуть плотно пригнанную пробку внутрь горлышка бутылки, заполненной водой по самую пробку.) Закон Бойля—Мариотта , наряду с законом Шарля , лег в основу Уравнения состояния идеального газа .

Дж. Трефил называет его «закон Бойля», однако мы предпочли принятое в российской традиции название закона. — Прим. переводчика .

См. также:

Robert Boyle, 1627-91

Англо-ирландский физик и химик. Родился в замке Лисмор (Lismore Castle), Ирландия, став четырнадцатым ребенком графа Коркского (Earl of Cork) — знаменитого авантюриста эпохи королевы Елизаветы. Окончив привилегированную Итонскую школу, где был одним из первых учеников среди «юных джентльменов», отправился в многолетнее путешествие по континентальной Европе, в ходе которого продолжил образование в Женевском университете. Вернувшись на родину в 1648 году, оборудовал частную лабораторию и занялся на ее базе физико-химическими исследованиями. В 1658 году перебрался в Оксфорд, где его учеником и ассистентом по лаборатории стал Роберт Гук (см. Закон Гука), будущий научный секретарь Королевского общества. Кстати, Бойль был одним из основателей и соучредителей Королевского общества, выросшего из кружка молодых оксфордских ученых. Провел целый ряд новаторских химических экспериментов, включая эксперименты по детальному изучению свойств кислот и оснований . По некоторым данным, первым выдвинул гипотезу о существовании химических элементов. Доказал, что воздух необходим для горения и дыхания. Помимо занятий наукой был соучредителем и членом-пайщиком «Восточно-индийской компании» и активно занимался миссионерской деятельностью в надежде обратить в христианство жителей восточных колоний Британской империи.

ЗАКОН БОЙЛЯ-МАРИОТТА

ЗАКОН БОЙЛЯ-МАРИОТТА , закон, согласно которому объем газа при постоянной температуре обратно пропорционален давлению. Это означает, что по мере возрастания давления объем газа уменьшается. Впервые этот закон был сформулирован в 1662 г. Робертом БОЙЛЕМ. Поскольку к его созданию причастен также французский ученый МАРИОТТ, в других странах, кроме Англии, этот закон называют двойным именем. Он представляет собой частный случай ЗАКОНА ИДЕАЛЬНОГО ГАЗА (описывающего гипотетический газ, идеально подчиняющийся всем законам поведения газов).

Когда некоторое количество газа подвергается сжатию, его давление повышается по мере уменьшения объема. Закон Бойля-Мариотта утверждает, что при любой заданной температуре произведение давления на объем остается неизменным как при сжатии, так и при расширении. На гра-фиш показаны эти соотно-шения. Газ, который бы в точности подчинялся этому закону, называемый идеальным газом, можно представить в виде скопления бесконечно малых, совершенно эластичных, сталкивающихся друг с другом частиц (наподобие стальных шарикоподшипников). Обозначения: Р - давление, V-объем, Т), Tj, Тз и т.д. - различные температуры (большие номера соответствуют более высоким температурам).

Научно-технический энциклопедический словарь .

Смотреть что такое "ЗАКОН БОЙЛЯ-МАРИОТТА" в других словарях:

Воздух (или инертный газ), находящийся в запечатанном пакете с печеньем расширяется, когда продукт поднят на значительную высоту над уровнем моря (ок 2000 м) Закон Бойля Мариотта один из основных газовых з … Википедия

Закон Бойля Мариотта один из основных газовых законов. Закон назван в честь ирландского физика, химика и философа Роберта Бойля (1627 1691), открывшего его в 1662, а также в честь французского физика Эдма Мариотта (1620 1684), который открыл… … Википедия

ЗАКОН БОЙЛЯ МАРИОТТА - один из основных газовых законов, согласно которому при постоянной температуре Т для данной массы m идеального (см.) произведение давления р на занимаемый им объём V есть величина постоянная: pV = const … Большая политехническая энциклопедия

закон Бойля-Мариотта - Boilio ir Marioto dėsnis statusas T sritis Standartizacija ir metrologija apibrėžtis Idealiųjų dujų dėsnis: suslėgtų dujų slėgio ir tūrio sandauga, kai temperatūra pastovi, nekinta, t. y. pV = const. Realiosioms dujoms galioja tik apytiksliai… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

закон Бойля-Мариотта - Boilio ir Marioto dėsnis statusas T sritis fizika atitikmenys: angl. Boyle and Mariotte law; Boyle Mariotte law vok. Boyle Mariottesches Gesetz, n rus. закон Бойля Мариотта, m pranc. loi de Boyle Mariotte, f … Fizikos terminų žodynas

закон Бойля-Мариотта и Гей-Люссака - Boilio, Marioto ir Gei Liusako dėsnis statusas T sritis fizika atitikmenys: angl. Boyle Charles law; Boyle Gay Lussac law vok. Boyle Charlessches Gesetz, n; Boyle Mariotte Gay Lussacsches Gesetz, n rus. закон Бойля Мариотта и Гей Люссака, m pranc … Fizikos terminų žodynas

Закон, связывающий изменения объема газа при постоянной температуре с изменениями его упругости. Этот закон, открытый в 1660 г. англ. физиком Бойлем и позже, но, независимо от него, Мариоттом во Франции, по своей простоте и определенности… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

закон бойля-маріотта - закон Бойля Мариотта Boyle’s and Mariotte’s law *Boyle Mariottesches Gesetz – закон iдеальних газiв, згiдно з яким добуток тиску на об єм незмiнної маси такого газу при сталiй температурi є величина стала: (pV) т = const. У певних межах… … Гірничий енциклопедичний словник

Уравнение состояния Статья является частью серии «Термодинамика». Уравнение состояния идеального газа Уравнение Ван дер Ваальса Уравнение Дитеричи Разделы термодинамики Начала термодинамики Уравнен … Википедия

Бойля Мариотта закон: произведение объёма данной массы идеального газа на его давление постоянно при постоянной температуре; установлен независимо Р. Бойлем (1662) и Э. Мариоттом (1676). * * * БОЙЛЯ МАРИОТТА ЗАКОН БОЙЛЯ МАРИОТТА ЗАКОН, один из… … Энциклопедический словарь

Книги

• Комплект таблиц. Физика. Молекулярно-кинетическая теория (10 таблиц) , . Учебный альбом из 10 листов. Броуновское движение. Диффузия. Агрегатные состояния тел. Опыт Штерна. Шкалы температур. Давление идеального газа. Закон Бойля-Мариотта. Закон Гей-Люссака. Закон…

В уроке 25 «» из курса «Химия для чайников » рассмотрим закон, связывающий давление и объем газа, а также графики зависимости давления от объема и объема от давления. Напомню, что в прошлом уроке « » мы рассмотрели устройство и принцип действия ртутного барометра, а также дали определение давлению и рассмотрели его единицы измерения.

(1627-1691), которому мы обязаны первым практически правильным определением химического элемента (узнаем в гл. 6), интересовался также явлениями, происходящими в сосудах с разреженным воздухом. Изобретая вакуумные насосы для выкачивания воздуха из закрытых сосудов, он обратил внимание на свойство, знакомое каждому, кому случалось накачивать камеру футбольного мяча или осторожно сжимать воздушный шарик: чем сильнее сжимают воздух в закрытом сосуде, тем сильнее он сопротивляется сжатию. Бойль называл это свойство «пружинистостью » воздуха и измерял его при помощи простого устройства, показанного на рис. 3.2, а и б.

Бойль запирал ртутью немного воздуха в закрытом конце изогнутой трубки (рис. 3-2, а) а затем сжимал этот воздух, понемногу добавляя ртуть в открытый конец трубки (рис. 3-2, б). Давление, испытываемое воздухом в закрытой части трубки, равно сумме атмосферного давления и давления столбика ртути высотой h (h - высота, на которую уровень ртути в открытом конце трубки превышает уровень ртути в закрытом конце). Полученные Бойлем данные измерения давления и объема приведены в табл. 3-1. Хотя Бойль не предпринимал специальных мер для поддержания постоянной температуры газа, по-видимому, в его опытах она менялась лишь незначительно. Тем не менее Бойль заметил, что тепло от пламени свечи вызывало значительные изменения свойств воздуха.

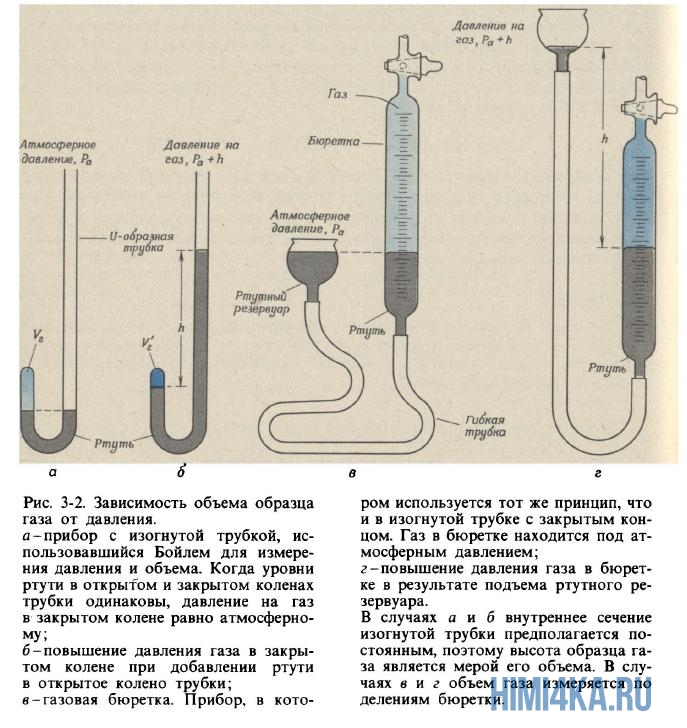
Анализ данных о давлении и объеме воздуха при его сжатии

Таблица 3-1 , которая содержит экспериментальные данные Бойля о взаимосвязи давления и объема для атмосферного воздуха, расположена под спойлером.

После того как исследователь получает данные, подобные приведенным в табл. 3-1, он пытается найти математическое уравнение , связывающее между собой две зависящие друг от друга величины, которые он измерял. Один из способов получения такого уравнения заключается в графическом построении зависимости различных степеней одной величины от другой в надежде получить прямолинейный график. Общее уравнение прямой линии имеет вид:

• y = ах + b (3-2)

где х и у - связанные между собой переменные, а a и b - постоянные числа. Если b равно нулю, прямая линия проходит через начало координат.

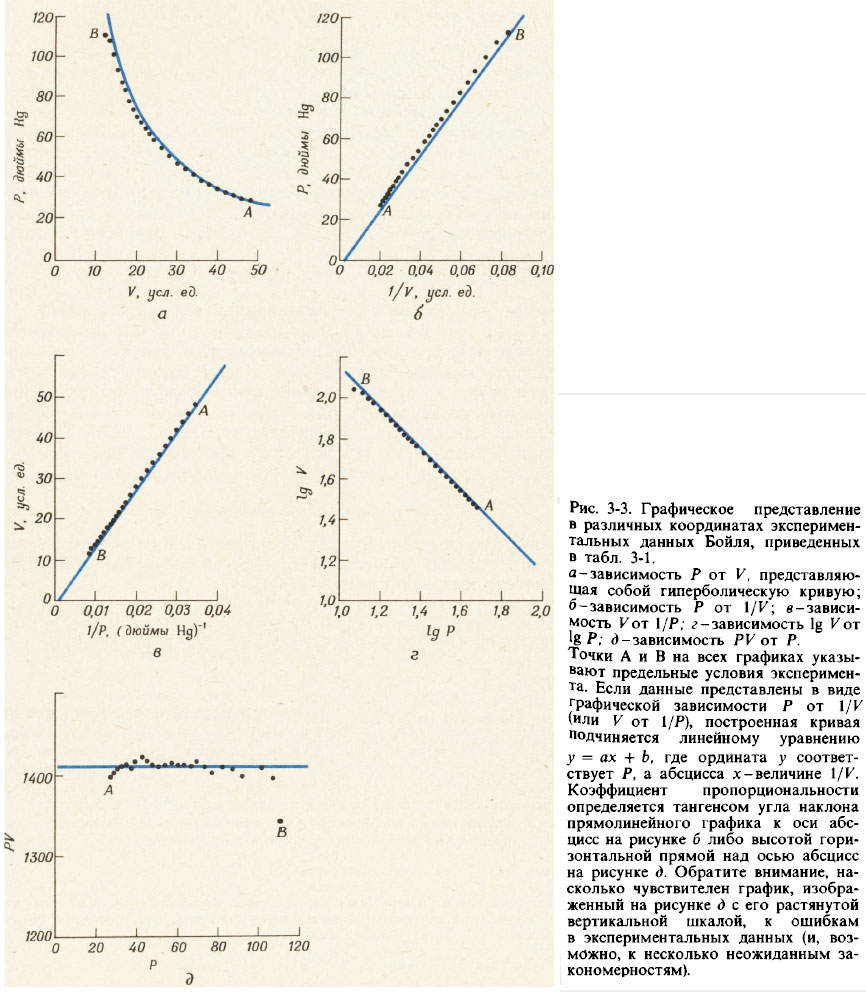
На рис. 3-3 показаны различные способы графического представления данных для давления Р и объема V, приведенных в табл. 3-1. Графики зависимости Р от 1/К и зависимости V от 1/Р представляют собой прямые линии, проходящие через начало координат. График зависимости логарифма Р от логарифма V также является прямой линией с отрицательным наклоном, тангенс угла которого равен — 1. Все эти три графика приводят к эквивалентным уравнениям:

• P = a / V (3-3а)
• V = a / P (3-3б)

• lg V = lg а - lg Р (3-3в)

Каждое из этих уравнений представляет собой один из вариантов закона Бойля-Мариотта , который обычно формулируется так: для заданного числа молей газа его давление пропорционально объему, при условии что температура газа остается постоянной .

Кстати, наверняка вам стало интересно, почему закон Бойля-Мариотта назван двойным именем. Это произошло так, потому что этот закон независимо от Роберта Бойля, который открыл его в 1662 году, был переоткрыт Эдмом Мариоттом в 1676 году. Вот так вот.

Когда взаимосвязь между двумя измеряемыми величинами проста до такой степени, как в данном случае, ее можно установить и численным способом. Если каждое значение давления Р умножить на соответствующее значение объема V, нетрудно убедиться, что все произведения для заданного образца газа при постоянной температуре оказываются приблизительно одинаковыми (см. табл. 3-1). Таким образом, можно записать, что

• P·V = а ≈ 1410 (3-3г)

Уравнение (З-Зг) описывает гиперболическую зависимость между величинами Р и V (см. рис. 3-3,а). Для проверки того, что построенный по экспериментальным данным график зависимости Р от V действительно соответствует гиперболе, построим еще дополнительный график зависимости произведения P·V от Р и убедимся, что он представляет собой горизонтальную прямую линию (см. рис. 3-3,д).

Бойль установил, что для заданного количества любого газа при постоянной температуре взаимосвязь между давлением Р и объемом V вполне
удовлетворительно описывается соотношением

• P·V = const (при постоянных Т и n) (3-4)

Формула из закона Бойля-Мариотта

Для сопоставления объемов и давлений одного и того же образца газа при различных условиях (но постоянной температуре) удобно представить закон Бойля-Мариотта в следующей формуле:

• P 1 ·V 1 = Р 2 ·V 2 (3-5)

где индексы 1 и 2 соответствуют двум различным условиям.

Пример 4. Доставляемые на плато Колорадо пластмассовые мешочки с пищевыми продуктами (см. пример 3) часто лопаются, потому что воздух, находящийся в них, при подъеме от уровня моря на высоту 2500 м, в условиях пониженного атмосферного давления, расширяется. Если предположить, что внутри мешочка при атмосферном давлении, соответствующем уровню моря, заключено 100 см 3 воздуха, какой объем должен занимать этот воздух при той же температуре на плато Колорадо? (Допустим, что для доставки продуктов используются сморщенные мешочки, не ограничивающие расширение воздуха; недостающие данные следует взять из примера 3.)

Решение
Воспользуемся законом Бойля в форме уравнения (3-5), где индекс 1 будем относить к условиям на уровне моря, а индекс 2 - к условиям на высоте 2500 м над уровнем моря. Тогда Р 1 = 1,000 атм, V 1 = 100 см 3 , Р 2 = 0,750 атм, а V 2 следует вычислить. Итак,

• P 1 ·V 1 = Р 2 ·V 2
• 1,000 атм · 100 см 3 = 0,750 атм · V 2

• V 2 = 133 см 3

Надеюсь, что после изучения урока 25 «» вы запомните зависимость объема и давления газа друг от друга.. Если у вас возникли вопросы, пишите их в комментарии. Если вопросов нет, то переходите к следующему уроку.